Sprężysto-plastyczność

Materiał ma cechy sprężyste, ale powyżej pewnej granicy naprężeń ich przyrost wiąże się z powstaniem dodatkowych niesprężystych odkształceń trwałych (to znaczy nie znikających przy zmniejszeniu naprężenia do zera).

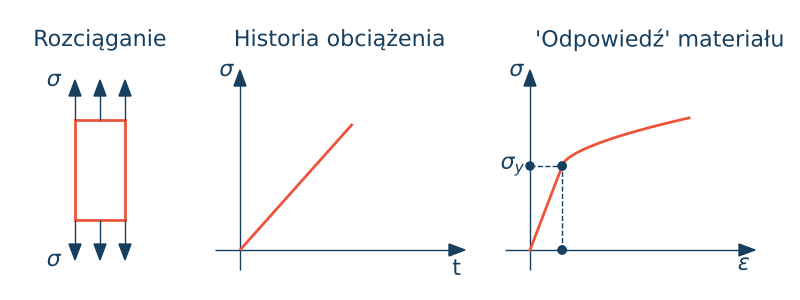
Pod odciążeniu materiału tj. gdy naprężenie jest równe zero w materiale pozostają odkształcenia trwała. Całkowite odkształcenie jest sumą odkształcenia sprężystego i plastycznego

$$\varepsilon = \varepsilon^e + \varepsilon^p, \quad \sigma = E \varepsilon^e$$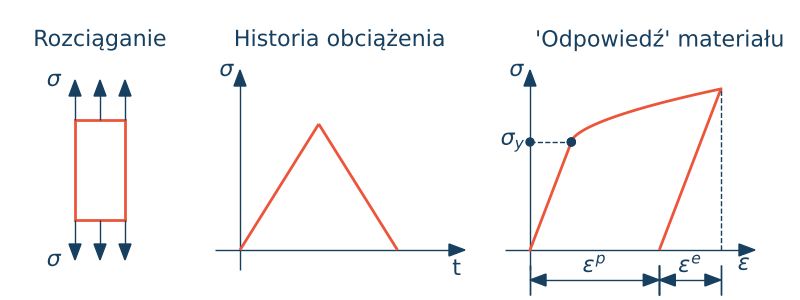

Ponowne przekroczenie granicy plastyczności jest już dla innej wartości granicy plastyczności $\sigma_y$. Granica plastyczności jest więc rosnącą funkcją odkształcenia plastycznego dla przykładu

$$\sigma_y = \sigma_{y0} + H \varepsilon^{p}$$

gdzie $H$ jest modułem wzmocnienia plastycznego

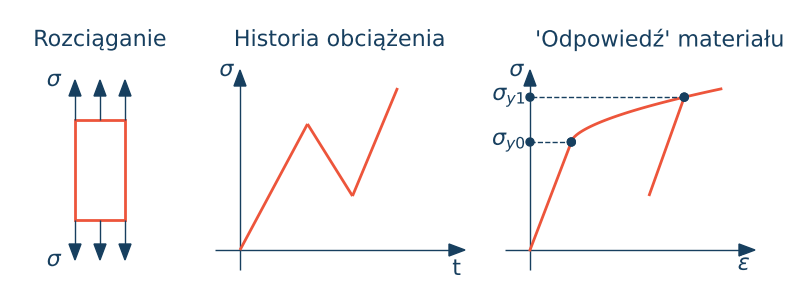
Ponowne przekorczenie granicy plastyczności przy zmianie znaku obciążenia. Modyfikujemy poprzedni wzór $\sigma_y = \sigma_{y0} + H\bar\varepsilon^{p}$, gdzie $\bar\varepsilon^{p}$ - skalarna miara odkształcenia plastycznego, w przypadku jednowymiarowym równa

$$\bar\varepsilon^{p} \int_0^t|\dot\varepsilon^{(p)}|dt$$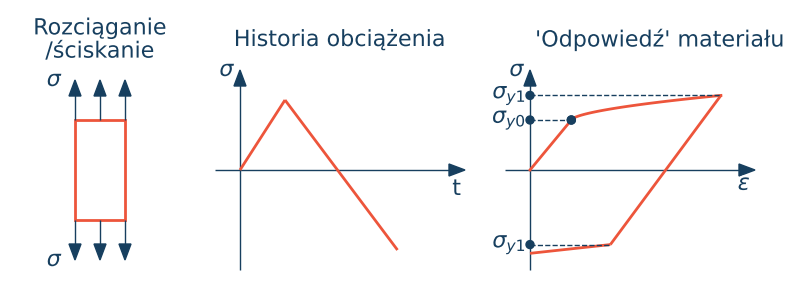

Przypadek trójwymiarowy

Zapisujemy analogicznie addytywny rozkład tensora odkształcenia na cześć sprężystą i plastyczną

$$\varepsilon_{ij}=\varepsilon_{ij}^{(e)}+\varepsilon_{ij}^{(p)}, \quad \sigma_{ij} = C_{ijkl}\varepsilon_{kl}^{e}$$

Równanie warunku plastyczności:

$$f(\ss,\bar\varepsilon^{p})= \bar\sigma-\sigma_y(\bar\varepsilon^{p}) \leq 0$$

tzn. jeśli $f<0$, to materiał zachowuje się jak sprężysty, gdzie np.

$$\sigma_y(\bar\varepsilon^{p})= \sigma_{y0} + \zeta\bar\varepsilon^{(p)}$$

gdzie $\bar\varepsilon^{(p)}$ oznacza tzw. ekwiwalentne odkształcenie plastyczne

$$\bar\varepsilon^{(p)} = \int_0^t \dot{\bar\varepsilon}{}^{p} \,dt, \qquad\dot{\bar\varepsilon}{}^{p} = \sqrt{\textstyle\frac23\dot\varepsilon_{ij}^{p}\dot\varepsilon_{ij}^{p}}$$

a $\bar\sigma$ to tzw. ekwiwalentne naprężenie Hubera--Misesa

$$\bar\sigma = \sqrt{\textstyle\frac32s_{ij}s_{ij}}\,, \qquad s_{ij} = \sigma_{ij} - \textstyle\frac13\sigma_{kk}\delta_{ij}$$

a $s_{ij}$ jest dewiatorem tensora naprężenia. Jeżeli $f=0$, to

$$\dot\varepsilon^{(p)}_{ij} = \lambda n_{ij}\,, \qquad n_{ij} = \frac{s_{ij}}{\sqrt{s_{kl}s_{kl}}} = \sqrt{\frac32}\frac{s_{ij}}{\bar\sigma}$$

co oznacza z definicji, że $\dot{\bar\varepsilon}{}^{p} = \sqrt{\frac23}\lambda$), gdzie współczynnik $\lambda$ można wyznaczyć z warunku

$$\dot f=0$ \begin{eqnarray*} \dot f &=& \pp{\bar\sigma}{s_{ij}}\,\dot s_{ij} - \sigma_y'\dot{\bar\varepsilon}{}^{(p)} = \sqrt{\frac32} \frac{\pp{s_{kl}}{s_{ij}}s_{kl}}{\sqrt{s_{mn}s_{mn}}} - \sigma_y'\sqrt{\frac23}\lambda = \sqrt{\frac32}n_{ij}\dot s_{ij} - \sigma_y'\sqrt{\frac23}\lambda \\* &=& \sqrt{\frac32}\left[n_{ij}\dot\sigma_{ij} - \textstyle\frac13\underbrace{n_{ij}\delta_{ij}}_{{}=0}\dot\sigma_{kk} - \frac23\sigma_y'\lambda \right] = \sqrt{\frac32}\left[ n_{ij}\dot\sigma_{ij} - \frac23\sigma_y'\lambda \right] = 0 \end{eqnarray*}$$

a więc

$$\lambda = \frac1h n_{ij}\dot\sigma_{ij}, \qquad h = \frac23\sigma_y'$$

W przypadku liniowego wzmocnienia $h=\frac23\zeta$, ogólnie jednak

$$h=h(\bar\varepsilon^{p}))$$

Zestawiając oba równania na relację między prędkością naprężenia a prędkościami obu części odkształcenia $\dot\varepsilon^{e}$ i $\dot\varepsilon^{p}$ otrzymujemy

$$\dot\sigma_{ij} = C_{ijkl}(\dot{\varepsilon}_{kl} - \dot{\varepsilon}^{(p)}_{kl}) = C_{ijkl}[\dot{\varepsilon}_{kl} - \frac1h n_{kl}(\dot\sigma_{mn}n_{mn})]$$

a po przekształceniach

$$\dot\sigma_{ij} = \left(C_{ijkl}-\frac{C_{ijmn} n_{mn} n_{pq} C_{pqkl}}{h+ n_{rs} C_{rstu} n_{tu}}\right)\dot{\varepsilon}_{kl} = C^{(e{-}p)}_{ijkl}\dot{\varepsilon}_{kl}$$

Jeśli izotropia to:

$$C^{(e{-}p)}_{ijkl} = \underbrace{\lambda\delta_{ij}\delta_{kl} +\mu( \delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk})}_{\displaystyle C_{ijkl}}-\frac{4\mu^2}{2\mu+h} n_{ij} n_{kl}$$