Sformułowanie lokalne zagadnienia nieliniowej termomechaniki ciała odkształcalnego

Ciało izotropowe, liniowe i sprężyste, (małe odkształcenia)

układ równań:

• równania ciągłości - $\dot\rho + \rho \dot{u}_{i,i} =0$

• równania ruchu $\sigma_{ij,j} + b_i = \rho\ddot{u}_i$

• równania geometryczne $\varepsilon_{ij} = \frac12(u_{i,j}+u_{j,i})$

• równania konstytutywne $\sigma_{ij} = 2\mu(\varepsilon_{ij}-aT\delta_{ij}) + \lambda (\varepsilon_{kk}-3aT)\delta_{ij}$

• równanie przewodnictwa $\rho c\dot T = (\lambda T_{,ii} + \rho r)$

Warunki początkowe muszą być zadane dla wszystkich niewiadomych pól w całym obszarze $\Omega$ i na brzegu $\partial \Omega$.

Warunki brzegowe różne typy warunków brzegowych definiujemy
na rozłącznych podobszarach $\partial \Omega_i$, takich, że $\bigcup_i\partial \Omega_i = \partial \Omega$. Najczęstsze typy to

• zadane przemieszczenia (war. Dirichleta), $u_i = \hat u_i(t)$ dla $\x\in\partial \Omega_u$
• zadane naprężenia (war. Neumanna), $\sigma_{ij}n_j = \hat t_i(t)$ dla $\x\in\partial \Omega_\sigma$
• inne typy - np. warunki kontaktowe:

Płaski stan naprężenie i odkształcenia

Tarczą nazywamy bryłę o jednym wymiarze (grubość) dużo mniejszym od pozostałych. W tarczy panuje płaski stan naprężenia (PSN).

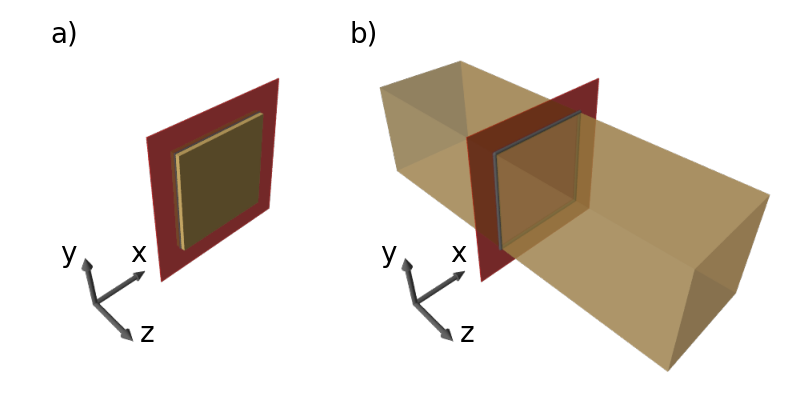
Dla płaskiego stanu naprężenia (PSN) i odkształcenia (PSO) tensory naprężenia i odkształcenia redukują sie do następującej postaci (zapis macierzowy)

$$[\ss] = [\sigma_{11}, \sigma_{22}, \sigma_{12}], \quad [\ee]=[\varepsilon_{11}, \varepsilon_{22}, 2\varepsilon_{12}]$$

Prawo Hooke'a dla materiału izotropowego redukuje sie dla (PSN) do postaci

a odwrotne prawo Hooke'a jest zdefiniowane jako

Odkształcenie w kierunku prostopadłym do płaszczyzny tarczy $\varepsilon_{33}$ jest w ogólności różne od zera i jest zależne od pozostałych składowych odkształcenia.

W przypadku płaskiego stanu odkształcenia zakładamy że odkształcenie w kierunku prostopadłym do rozpatrywanej płaszczyzny jest równe zero. Założenie to prowadzi do następującego związku konstytutywnego

Odwrotne prawo Hooke'a dla płaskiego stanu odkształcenia jest następujace

Zasada prac wirtualnych

Przepiszmy układ równań mechaniki w najprostszym liniowym przypadku:

$$\left.\begin{array}{@{}l} \sigma_{ij,j} + b_i = 0\\ \sigma_{ij} = f(\varepsilon_{kl})\\ \varepsilon_{kl} = \frac12(u_{k,l} + u_{l,k}) \end{array}\right\}\;\;x_i\in\Omega$$

Powyższy układ równań różniczkowych w celu ich jednoznacznego rozwiązania wymaga warunków brzegowych

$$\sigma_{ij}n_j = \hat{t}_i \, x_i \in \partial\Omega_{\sigma}\quad. u_i = \hat{u}_i \, x_i \in \partial\Omega_u, \quad \partial\Omega=\partial\Omega_u + \partial\Omega_{\sigma}$$

Jest to tzw. sformułowanie lokalne (mocne) zagadnienia, z niewiadomymi $\sigma_{ij}$, $\varepsilon_{kl}$ i $u_k$ (ale ,,efektywnie'' tylko~$u_k$, bo pozostałe można łatwo wyrugować i zapisać $\sigma_{ij} = \sigma_{ij}(u_k)$ w równaniu 1 i w warunku brzegowym)

Definiujemy dwa zbiory funkcji (pól wektorowych), ciągłe i różniczkowalne w zakresie wymaganym przez dalsze przekształcenia:

$$\mathcal{P} = \left\{\; \u(\x),\;\x\in\Omega \colon \u=\hat{\u}\;\;\mbox{dla $\x\in\partial \Omega_u$} \; \right\}$$ $$\mathcal{W} = \left\{\; \delta\u(\x),\;\x\in\Omega \colon \delta\u = 0\;\;\mbox{dla $\x\in\partial\Omega_u$}\,, \; \underset{\x}{\forall} | \delta\u(\x)| < \epsilon \; \right\}, \qquad \epsilon>0.$$

Oczywiście, jeśli istnieje rozwiązanie zagadnienia lokalnego, to należy ono do zbioru $\mathcal{P}$. Łatwo zauważyć, że

$$\forall_{\u\in\mathcal{P}, \, \delta\u\in\mathcal{W}}, \quad \u+\delta\u \in \mathcal{P}$$

Skoro $\u(\x)$ spełnia kinematyczne warunki brzegowe to wartość wariacji przemieszcenia na brzegu $\partial\Omega_u$ musi być równa zero. Dla wystarczająco małej wartości $\epsilon$ będziemy traktowali $\mathcal{W}$ jako zbiór infinitezymalnych wariacji (zaburzeń) funkcji ze zbioru $\mathcal{P}$.

Przemnażając obustronnie równanie równowagi przez wirtualne przemieszczenia dostajemy

$$\sigma_{ij,j}\delta u_i + b_i \delta u_i = 0$$

Całkujemy po obszarze $\Omega$

$$\int_{\Omega}\left[ \sigma_{ij,j}\delta u_i + b_i \delta u_i\right] dV = 0$$

Człon $\sigma_{ij,j}\delta u_i$ możemy zastąpić przez

$$\sigma_{ij,j}\delta u_i = \left(\sigma_{ij}\delta u_i\right)_{,j} - \sigma_{ij} \delta u_{i,j}$$

ponieważ wykorzystując wzór na iloczyn pochodnej mamy $\left(\sigma_{ij}\delta u_i\right)_{,j} = \sigma_{ij,j}\delta u_i + \sigma_{ij} \delta u_{i,j}$

Wstawiając otrzymane wyrażenie do całki otrzymujemy

$$\int_{\Omega} \left(\sigma_{ij}\delta u_i\right)_{,j} dV + \int_{\Omega} b_i \delta u_i dV = \int_{\Omega} \sigma_{ij} \delta u_{i,j} dV$$

Wykorzystując twierdzenie Gaussa-Ostrogradskiego pierwszą całkę możemy zamienić na całkę po brzegu ciała

$$\int_{\Omega} \left(\sigma_{ij}\delta u_i\right)_{,j} dV = \int_{\partial\Omega} \sigma_{ij} n_j \delta u_i dS$$

Wariacja przemieszczeń na brzegu ciała $\Omega_u$ jest równa zero. Na brzegu $\Omega_{\sigma}$ wykorzystując warunki brzegowe mamy $\sigma_{ij}n_j = \hat{t}_i$. Ostatecznie pierwsza całka jest równa

$$\int_{\Omega} \left(\sigma_{ij}\delta u_i\right)_{,j} dV = \int_{\partial\Omega_{\sigma}} \hat{t}_i \delta u_i dS$$

Wykorzystują symetrię tensora naprężenia możemy zapisać, że

$$\sigma \delta u_{i,j} = \cfrac12\left( \sigma_{ij}u_{i,j} + \sigma_{ji}u_{i,j} \right) = \cfrac12\left( \sigma_{ij}u_{i,j} + \sigma_{ij}u_{j,i} \right) = \sigma_{ij} \cfrac12 \left( u_{i,j} + u_{j,i}\right) = \sigma_{ij}\delta\varepsilon_{ij},$$

gdzie $\delta\varepsilon_{ij}$ jest tensorem odkształcenia odpowiadającym przemieszczeniu wirtualnemu. Ostatecznie zasada prac wirtualnych może być zapisana jako

$$\int_{\Omega} \sigma_{ij}\delta\varepsilon_{ij} = \int_{\partial\Omega_{\sigma}} \hat{t}_i \delta u_i dS + \int_{\Omega} b_i \delta u_i dV$$

co możemy przetłumaczy jako

Praca sił wewnętrznych (rzeczywistych naprężeń na wirtualnych odkształceniach) jest równy pracy sił zewnętrznych (rzeczywistych sił powierzchniowych i objętościowych na wirtualnych przemieszeniach). Zasada prac wirtualnych jest zawsze spełniona dla dowolnego przemieszczenia wirtualnego.