Zagadnienia przewodnictwa ciepła

• Energia cieplna: prędkość energii ciepła dostarczonego do układu (ciała)

$$\dot{Q} = -\int_{d \Omega} q_in_i\, dS + \int_{\Omega} \rho r\, dV$$

gdzie $q_i$ - składowe wektora strumienia ciepła odniesione do jednostki powierzchni i czasu, $r$ - moc wewnętrznych źródeł ciepła na jednostkę masy. Iloczyn $q_in_i$ jest ujemny gdy strumień ciepła jest skierowany przeciwnie do normalnej dlatego w pierwszej całce pojawia się znak minus.

• prędkość energii ciepła gromadzonej w ciele

$$\dot{E_T} = \int_{\Omega} \rho \dot e_T \, dV$$

gdzie $e_T$ - gęstość energii wewnętrznej związanej ze zmagazynowanym w materiale ciepłem na jednostkę masy. Energia wewnętrzna jest proporcjonalna do zmiany temperatury $T(\x,t)$ według następującej zależności

$$\dot e_T = c\dot T,$$

gdzie $c$ - ciepło właściwe (stała materiałowa). W powyższym wzorze $\dot T$ oznacza pochodną materialną!. Wzór wiążący enregię wwewnętrzną ze zmianą temperatury jest prawdzy gdy brak jest przemian fazowych w materiale. Materiał nie przechodzi przez żadną przemianę fazową (np. topnienie, parowanie) w rozpatrywanym zakresie temperatury. Przemiany fazowe absorbują lub uwalniają energię cieplną, nie zmieniając przy tym temperatury materiału.

• Przy braku zjawisk mechanicznych musi być $\dot Q = \dot E_T$, czyli stosując twierdzenie Gaussa-Ostrogradskiego mamy

$$\dot{E_T} - \dot{Q} = \int_{\Omega} \rho \dot e_T \,dV + \int_{d \Omega} q_in_i\, d A - \int_{\Omega} \rho r\,d V = \int_{\Omega} (\rho \dot{e_T} + q_{i,i} - \rho r)\, d V = 0$$

skąd, po uwzględnieniu dowolności obszaru całkowania, otrzymujemy lokalne (różniczkowe) równanie bilansu energii cieplnej

$$\rho \dot{e_T} = - q_{i,i} + \rho r = -\div \q + \rho r$$

Na podstawie równania bilansu energii cieplnej możemy podzielić energię wewnętrzną na część mechaniczną i termiczną i zapisać

$$\rho\dot e =\underbrace{\sigma_{ij}\dot\varepsilon_{ij}}_{\textstyle\rho\dot e_M} \underbrace{{}- q_{i,i} + \rho r}_{\textstyle\rho\dot e_T}$$

• prawo przewodzenia (prawo konstytutywne przepływu ciepła) - np. liniowe prawo Fouriera

$$\q = - \ll \nabla T, \qquad q_i = -\lambda_{ij}T_{,j}$$

gdzie $\ll$ tensor przewodności cieplnej (stała materiałowa). Dla materiałów izotropowych $\ll = \lambda\I$, czyli $\lambda_{ij} = \lambda\delta_{ij}$ ($\lambda$ -- skalarny współczynnik przewodności cieplnej) -- wtedy prawo Fouriera ma postać

$$\q = - \lambda\nabla T, \qquad q_i = -\lambda T_{,i}$$

Równanie przewodnictwa

Podstawiając prawo przewodzenia do równania energii otrzymujemy r-nie przewodnictwa, w tym przypadku zwane r-niem Fouriera--Kirchhoffa, z jedną niewiadomą $T(\x,t)$: dla ogólnego przypadku anizotropii

lub, dla przypadku izotropii,

$$\rho c\dot T = \div(\lambda\nabla T) + \rho r = (\lambda T_{,i})_{,i} + \rho r$$

przypadki szczególne:

• jeżeli współczynnik przewodności (skalarny lub tensorowy) nie jest funkcją $\x$ (jednorodność), to wyłączamy go przed operator dywergencji, otrzymując dla ogólnego przypadku anizotropii

$$\rho c\dot T = \ll \cdot (\nabla\otimes\nabla T) + \rho r = \lambda_{ij}T_{,ij} + \rho r$$

lub, dla przypadku izotropii,

$$\rho c\dot T = \lambda\Delta T + \rho r = \lambda T_{,ii} + \rho r$$

jeżeli $\dot T = 0$ (założenie to jest z dobrą dokładnością spełnione przy ustalonych warunkach brzegowych po upływie odpowiednio długiego czasu) to przepływ nazywamy ustalonym, a w równaniu przewodnictwa znika lewa strona.

jeżeli przepływ jest ustalony, współczynnik przewodności izotropowy jednorodny, oraz nie ma źródeł ciepła, to otrzymujemy r-nie Laplace'a

$$\Delta T = 0$$

Typy warunków brzegowych i początkowych

• warunki początkowe -- zadana wartość pola temperatury we wszystkich punktach obszaru $\Omega$:

$$T(\x,0) = T^0(\x)$$

• warunki brzegowe

1) zadana temperatura na brzegu ciała,

$$T = \hat{T} \quad \text{dla} \quad \x\in d \Omega_T$$

2) zadany przepływ,

$$-q_in_i\; ({}=\lambda_{ij}T_{,j}n_i) = \hat q + q^c(T) + q^r(T)\quad \text{dla} \quad \x\in d\Omega_q$$

3) konwekcja:

$$q^c = \alpha(T_{\infty} - T)$$

4) radiacja:

$$q^r = \tilde h(T^4_r - T^4)$$

oczywiście

$$d\Omega = d \Omega_T\cup d \Omega_q, \emptyset = d \Omega_T \cap d \Omega_q$$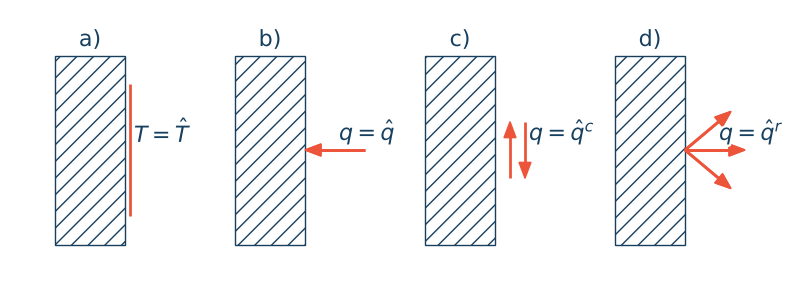

Sprzężenia termo-mechaniczne

• równanie konstytutywne: (i) stałe materiałowe, szczególnie w plastyczności i lepko-sprężystości, mogą zależeć od temperatury, (ii) zmiany temperatury powodują dodatkowe odkształcenia (rozszerzalność cieplna); przy dużych zmianach temperatury wpływa to na rozwiązanie zagadnienia mechaniki.
• równanie przewodnictwa: określone jest na aktualnej geometrii, która jest funkcją pola przemieszczeń -- przy dużych deformacjach wpływa to na rozwiązanie tego równania
• nieodwracalne procesy w materiale (plastyczność, lepkość), które powodują dysypację energii, generują tym samym ciepło, a więc w r-niu przewodnictwa $r = r(\u)$

Sprzężenie jednostronne: rozszerzalność cieplna

Kiedy materiał podlega zmianie temperatury, rozszerza się lub kurczy. Wielkość rozszerzenia lub kurczenia jest zazwyczaj charakteryzowana przez tensor rozszerzalność cieplnej $\a$, który jest miarą zmiany długości w danym kierunku przy zmianie temperatury o $1^{\circ}C$. Dla ciała bez naprężeń deformacje powstałą w wyniku zmiany temperatury możemy opisać jako

$$\F^{(T)} = \I+\a T$$

gdzie $T$ to temperatura względna (różnica między temperaturą rzeczywistą a temperaturą odniesienia, przy której $\F^{(T)} = \I$).

Jeżeli materiał jest izotropowy pod względem termicznym to wtedy tensor rozszerzalności cieplnej możemy wyrazić jako tensor kulisty tj. $\quad \a=a\I$, gdzie $a$ to współczynnik rozszerzalności cieplnej. Gradient deformacji dla takiego materiału wyraża się następująco

$$\F^{(T)} = (1+aT)\I$$

Obliczmy gradient przemieszczenia dla deformacji wywołanej rozszerzalnością cieplną dla przypadku ogólnego

$$u^{(T)}_{i,j}=F^{(T)}_{ij}-\delta_{ij}=a_{ij}T.$$

Tensor małego odkształcenia jest równy

$$\varepsilon^{(T)}_{ij} = \frac12(u^{(T)}_{i,j}+u^{(T)}_{j,i}) = a_{ij}T$$

Jeśli w materiale pojawiają się naprężenia, to dokonujemy multiplikatywnego rozkładu gradientu deformacji na cześć związaną z naprężeniem $\F^{(\sigma)}$ oraz temperaturą $\F^{(T)}$

$$\F=\F^{(\sigma)}\F^{(T)}$$

Obliczmy gradient przemieszczenia dla powyższej sytuacji

$$u_{i,j}=F_{ij}-\delta_{ij} = \left( \pp{u^{(\sigma)}_i}{x_k}+ \delta_{ik}\right) \left( \pp{u^{(T)}_k}{x_j}+ \delta_{kj}\right) - \delta_{ij}$$

Rozpisując wzór dostajemy

$$u_{i,j} = \pp{u^{(\sigma)}_i}{x_j} + \pp{u^{(T)}_i}{x_j} + \pp{u^{(\sigma)}_i}{x^k}\,\pp{u^{(T)}_k}{x_j}$$

Dla małych deformacji możemy pominąć człon nieliniowy, wtedy tensor małego odkształcenia jest równy

$$\varepsilon_{ij} = \varepsilon^{(T)}_{ij} + \varepsilon^{(\sigma)}_{ij}$$

Wprzypadku liniowej sprężystości i małych deformacji związek konstytutywny możemy zapisać jako

$$\ss= \C\ee^{(\sigma)}= \C\cdot(\ee-\a T) = \C\cdot\ee - \C\cdot\a T$$

Odwrotne prawo mażemy zapisać następująco

$$\ee = \D\cdot\ss + \a T, \qquad \D = \C^{-1}.$$

Jeżeli warunki brzegowe uniemożliwiają powstanie odkształceń, to podgrzanie materiału do $T$ spowoduje powstanie naprężeń
$$\sigma_{11}=\sigma_{22}=\sigma_{33} = -\frac{EaT}{1-2\nu} = -3K\,aT$$

gdzie $K = \cfrac{E}{3(1-2\nu)}$ to moduł ściśliwości. Pozostałe składowe tensora naprężenia są równe zero, ($\sigma_{12}=\sigma_{23}=\sigma_{13}=0$). Zwróćmy uwagę na znak "$-$" oraz że dla $\nu=\frac12$ (materiał nieściśliwy) naprężenia będą nieskończenie wielkie.

Sprzężenie dwustronne

• Efekty mechaniczne na stan termiczny

Ciepło deformacji: Podczas odkształcenia plastycznego część energii mechanicznej jest przekształcana w ciepło, co prowadzi do lokalnego wzrostu temperatury. Ten efekt jest szczególnie istotny w przypadku dużych odkształceń plastycznych, gdzie generacja ciepła może być znaczna.

Efekt piezokaloryczny: Deformacja mechaniczna może prowadzić do zmiany objętości materiału, co wpływa na jego stan termiczny. Na przykład rozciąganie materiału może prowadzić do jego ochłodzenia, podczas gdy ściskanie może prowadzić do jego nagrzania.

• Efekty termiczne na stan mechaniczny

Termoplastyczność: Wzrost temperatury może zmniejszać wytrzymałość materiału na odkształcenia plastyczne, co powoduje, że materiał łatwiej poddaje się deformacji plastycznej. Wzrost temperatury może obniżyć granicę plastyczności materiału, co skutkuje wcześniejszym przejściem od zachowania sprężystego do plastycznego.

Relaksacja naprężeń: Wzrost temperatury może prowadzić do relaksacji naprężeń w materiale. Materiały sprężysto-plastyczne mogą poddawać się relaksacji naprężeń, co oznacza, że naprężenia zmniejszają się z czasem w stałej temperaturze.

Zmiana właściwości materiału: Temperatura wpływa na moduł sprężystości i inne właściwości mechaniczne materiału. Na przykład, w wysokich temperaturach materiały mogą wykazywać zmniejszoną sztywność, co wpływa na ich zachowanie mechaniczne.