Jednowymiarowe modele ośrodków ciągłych

Pełzanie i relaksacja

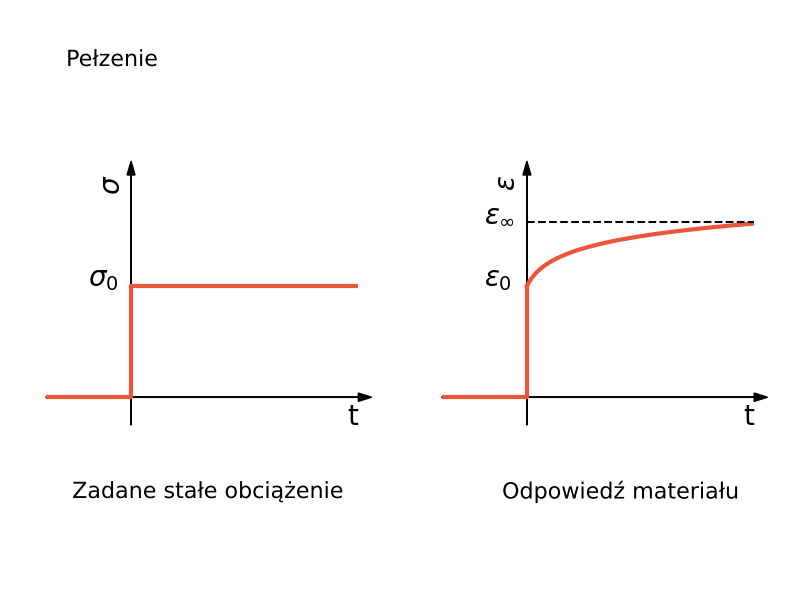
• próba pełzania, gdy zadane jest stałe w czasie naprężenie lub-w ścisłym zapisie formalnym-gdy zadana jest następująca historia naprężenia

$$\sigma(t) = \sigma_0 H(t)$$

gdzie $H(t)$ to funkcja Haviside'a. Pochodną funkcji Haviside'a jest funkcja Diraca $\delta(t)$.

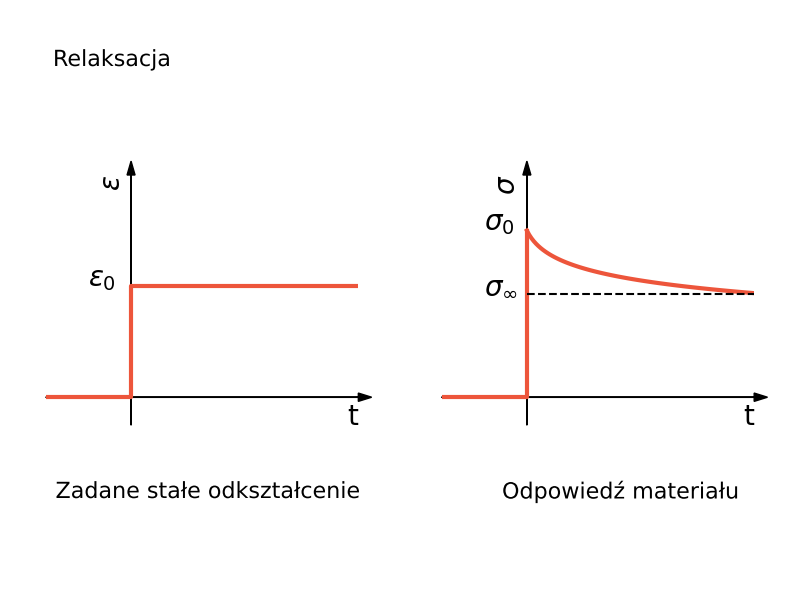
• próba relaksacji, gdy zadana jest historia odkształcenia $\varepsilon(t) = \varepsilon_0 H(t)$

Modele jednoparametrowe

• ciało Hooke'a - model ciała liniowo sprężystego

$$\sigma(t) = E\varepsilon(t)$$

Sprawdźmy jak model ten zachowuje się w próbie pełzania i relaksacji. Po podstawieniu stałej w czasie historii obciążenia oraz odkształcenia dostajemy odpowiednio

pełzanie: $\varepsilon(t) = \cfrac{\sigma_0}{E} H(t)$
relaksacja:$\sigma(t)= E\varepsilon_0 H(t)$
Model Hooke'a nie opisuje więc relaksacji ani pełzania.

• model (ciecz lepka) Newtona - liniowa lepkość

$$\sigma(t) = \eta\dot{\varepsilon}(t)$$

pełzanie: $\varepsilon(t) = \cfrac{\sigma_0}{\eta}t + \varepsilon(0)$
relaksacja: $\sigma(t) = \eta\varepsilon_0\delta(t)$

Pełzanie przebiega ze stałą prędkością (pełzanie ustalone) i dla $t \rightarrow \infty$ odkształcenie $\varepsilon \rightarrow \infty$ (pełzanie nieograniczone). Odpowiedzią materiału w próbie relaksacji jest impuls $\sigma(0) \rightarrow \infty$, po czym następuje całkowita, natychmiastowa relaksacja naprężeń do wartości 0.

Modele dwuparametrowe

Modele wieloparametrowe (w tym i dwuparametrowe) konstruuje się, dokonując połączenia szeregowego lub równoległego poszczególnych modeli podstawowych.

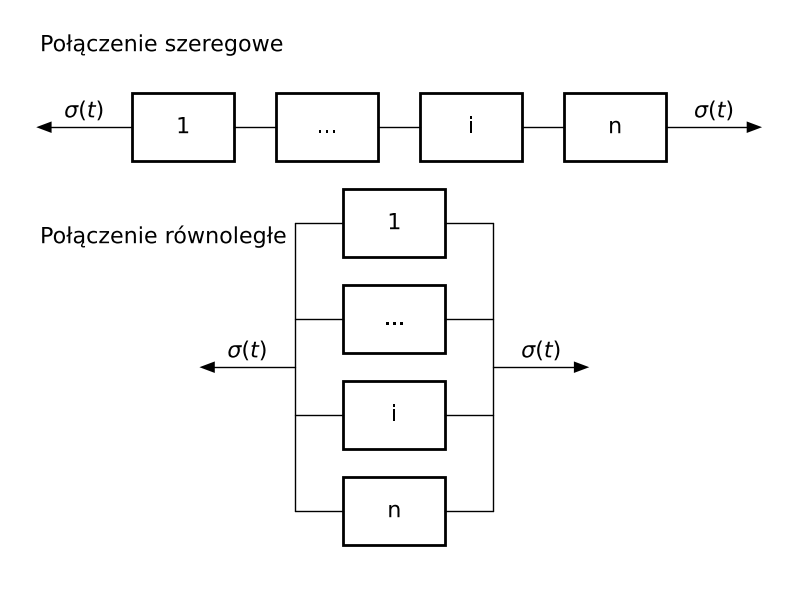
Dla połączenia szeregowego:
• równanie równowagi $\Rightarrow \sigma_i = \sigma$
• równanie nierozdzielności odkształceń $\Rightarrow \varepsilon = \sum\limits_{i=1}^{n}\varepsilon_i$

Dla połączenia równoległego:
• równanie równowagi $\Rightarrow \sigma = \sum\limits_{i=1}^{n}\sigma_i$
• równanie nierozdzielności odkształceń $\Rightarrow \varepsilon = \varepsilon_i$

Wybrane modele dwuparametrowe

• model Maxwella - jest szeregowym połączeniem ciała Hooke'a i cieczy Newtona

$$\dot{\varepsilon}(t) = \cfrac{\dot{\sigma}(t)}{E} + \cfrac{\sigma(t)}{\eta}$$

pełzanie $\varepsilon(t) = \cfrac{\sigma_0}{E} + \cfrac{\sigma_0}{\eta}t$
relaksacja $\sigma(t) = \sigma(0) \exp\left( -\cfrac{E}{\eta}t\right)$

Model ten opisuje nieograniczone pełzanie ustalone z początkowym odkształceniem natychmiastowym, określonym przez wielkość natychmiastowego modułu sprężystości $E$. W próbie relaksacji $t \rightarrow \infty$ dostajemy $\sigma \rightarrow 0$, a więc model opisuje relaksację zupełną

• model Kelvina - jest równoległym połączeniem ciała Hooke'a i cieczy Newtona.

$$\sigma(t) = E\varepsilon(t) + \eta \dot{\varepsilon}(t)$$

pełzanie $\varepsilon(t) = \cfrac{\sigma_0}{E} \left[1-\exp \left(-\cfrac{E}{\eta}t\right)\right]$, relaksacja $\sigma(t) = E\varepsilon_0 H(t) +\eta \varepsilon_0 \delta(t)$