Równania konstytutywne
Bilans równań i niewiadomych (w konfiguracji aktualnej $C_t$):
$$\dot{\rho} + \rho v_{i,i} = 0$$Równanie równowagi dynamicznej (zasada zachowania pędu)
$$\sigma_{ij,j} + b_i = \rho a_{i}$$Związki geometryczne
$$\varepsilon_{ij} = \cfrac{1}{2}\left( \delta_{ij} - c_{ij}\right)$$Niewiadome występujące w tych równaniach to naprężenie, odkształcenie, przemieszczenie, gęstość razem 16 niewiadomych a mamy tylko 10 równań. Brakuje 6 równań wiążących naprężenia z pozostałymi niewiadomymi – są to równania konstytutywne, w ogólnej postaci
$$f(\rho, \varepsilon_{kl} , \sigma_{kl} , \dot{\rho}, \dot{\varepsilon}_{kl}, \dot{\sigma}_{kl}, t, . . .) = 0$$Materiał sprężysty
Materiałem sprężystym nazywamy taki materiał, w którym aktualny stan naprężenia w danej cząstce zależy wyłącznie od aktualnej deformacji, a nie od jej historii, czyli poprzednich deformacji ciała. Odkształcone ciało sprężyste po usunięciu obciążenia wraca do swojego pierwotnego kształtu. Postulowana funkcja $f$ musi być więc bijekcją
$$\ss(t) = f(\ee(t))$$Sprężystość liniowa
Dla tego typu materiałów zależność naprężenia od odkształcenia jest liniowa.
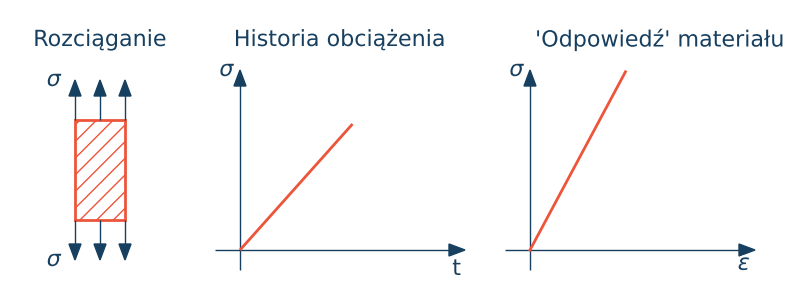
Konfiguracja aktualna jest bliska konfiguracji początkowej, zanika różnica między opisem materialnym i przestrzennym $\X \approx \x$. Związek między odkształceniem a naprężeniem opisany jest przez prawo Hooke'a
$$\ss = \C \cdot \ee \qquad \sigma_{ij} = C_{ijkl} \varepsilon_{kl},$$gdzie $C_{ijkl}$ tensor sztywności (4-go rzędu) będący stałą materiałową, w określonym układzie współrzędnych opisany przez tablicę $3 \times 3 \times 3 \times 3 = 81$ liczb; można to zapisać w postaci następującego wzoru wektorowo-macierzowego:
$$\def\arraycolsep{3pt} \left\{\begin{array}{c} \sigma_{11}\\\sigma_{22}\\\sigma_{33}\\ \sigma_{12}\\\sigma_{23}\\\sigma_{31}\\\hline \sigma_{21}\\\sigma_{32}\\\sigma_{13} \end{array}\right\} = \left[\begin{array}{cccccc|ccc} C_{1111}&C_{1122}&C_{1133}&C_{1112}&C_{1123}&C_{1131}&C_{1121}&C_{1132}&C_{1113}\\ C_{2211}&C_{2222}&C_{2233}&C_{2212}&C_{2223}&C_{2231}&C_{2221}&C_{2232}&C_{2213}\\ C_{3311}&C_{3322}&C_{3333}&C_{3312}&C_{3323}&C_{3331}&C_{3321}&C_{3332}&C_{3313}\\ C_{1211}&C_{1222}&C_{1233}&C_{1212}&C_{1223}&C_{1231}&C_{1221}&C_{1232}&C_{1213}\\ C_{2311}&C_{2322}&C_{2333}&C_{2312}&C_{2323}&C_{2331}&C_{2321}&C_{2332}&C_{2313}\\ C_{3111}&C_{3122}&C_{3133}&C_{3112}&C_{3123}&C_{3131}&C_{3121}&C_{3132}&C_{3113}\\\hline C_{2111}&C_{2122}&C_{2133}&C_{2112}&C_{2123}&C_{2131}&C_{2121}&C_{2132}&C_{2113}\\ C_{3211}&C_{3222}&C_{3233}&C_{3212}&C_{3223}&C_{3231}&C_{3221}&C_{3232}&C_{3213}\\ C_{1311}&C_{1322}&C_{1333}&C_{1312}&C_{1323}&C_{1331}&C_{1321}&C_{1332}&C_{1313} \end{array}\right]\!\! \left\{\begin{array}{c} \varepsilon_{11}\\\varepsilon_{22}\\\varepsilon_{33}\\ \varepsilon_{12}\\\varepsilon_{23}\\\varepsilon_{31}\\\hline \varepsilon_{21}\\\varepsilon_{32}\\\varepsilon_{13} \end{array}\right\}$$Sens fizyczny – każdy współczynnik tensora $\C$ opisuje sztywność materiału na określony kierunek obciążenia i towarzyszącą mu postać deformacji (wymiar: [Pa])
Z symetrii $\sigma_{ij}$ i $\varepsilon_{kl}$ wynika odpowiednio $C_{ijkl} = C _{jikl}$ i $C_{ijkl} = C_{ijlk}$ - możemy więc usunąć 3 ostatnie wyrazy wektorów $\ss$ i $\ee$ oraz 3 ostatnie wiersze i kolumny macierzy $\C$ (pamiętając o pomnożeniu odkształceń postaciowych przez 2) możemy użyć również definicji kąta odkształcenia postaciowego $\varepsilon_{12} = \cfrac{1}{2}\gamma$) spośród 81 zostaje tylko 36 niezależnych stałych materiałowych.
$$\left\{\begin{array}{c} \sigma_{11}\\\sigma_{22}\\\sigma_{33}\\ \sigma_{12}\\\sigma_{23}\\\sigma_{31}\end{array}\right\} = \left[\begin{array}{cccccc} C_{1111}&C_{1122}&C_{1133}&C_{1112}&C_{1123}&C_{1131}\\ C_{2211}&C_{2222}&C_{2233}&C_{2212}&C_{2223}&C_{2231}\\ C_{3311}&C_{3322}&C_{3333}&C_{3312}&C_{3323}&C_{3331}\\ C_{1211}&C_{1222}&C_{1233}&C_{1212}&C_{1223}&C_{1231}\\ C_{2311}&C_{2322}&C_{2333}&C_{2312}&C_{2323}&C_{2331}\\ C_{3111}&C_{3122}&C_{3133}&C_{3112}&C_{3123}&C_{3131} \end{array}\right] \left\{\begin{array}{c} \varepsilon_{11}\\\varepsilon_{22}\\\varepsilon_{33}\\ 2\varepsilon_{12}\\2\varepsilon_{23}\\2\varepsilon_{31}\end{array}\right\}$$ $$\ss_{6 \times 1} = \C_{6\times6} \, \ee_{6\times 1}$$Jeżeli istnieje funkcja energii sprężystej to wtedy 21 stałych bo uwzględniamy symetrię $C_{ijkl}=C_{klij}$:
$$\left\{\begin{array}{c} \sigma_{11}\\\sigma_{22}\\\sigma_{33}\\ \sigma_{12}\\\sigma_{23}\\\sigma_{31}\end{array}\right\} = \left[\begin{array}{cccccc} C_{1111}&C_{1122}&C_{1133}&C_{1112}&C_{1123}&C_{1131}\\ &C_{2222}&C_{2233}&C_{2212}&C_{2223}&C_{2231}\\ & &C_{3333}&C_{3312}&C_{3323}&C_{3331}\\ & & &C_{1212}&C_{1223}&C_{1231}\\ & & & &C_{2323}&C_{2331}\\ sym & & & & & C_{3131} \end{array}\right] \left\{\begin{array}{c} \varepsilon_{11}\\\varepsilon_{22}\\\varepsilon_{33}\\ 2\varepsilon_{12}\\2\varepsilon_{23}\\2\varepsilon_{31}\end{array}\right\}$$ $$\ss_{6 \times 1} = \C_{6\times6} \, \ee_{6\times 1}$$Energia odkształcenia na jednostkę objętości jest równa
$$dU = \sigma_{ij}d\varepsilon_{ij}$$i ma charakter potencjalny tzn.
$$U = \cfrac12 C_{ijkl}\varepsilon_{ij}\varepsilon_{kl} \rightarrow C_{ijkl} = \pp{^2U}{\varepsilon_{ij}\partial \varepsilon_{kl}}$$Symetrie materiału
Grupą symetrii materiału nazywamy zbiór takich obrotów, jakim możemy poddać element objętości rozważanego materiału $dV$ w stosunku do dowolnego nałożonego na ten element obciążenia, które nie zmienią odpowiedzi materiału
• Anizotropia (21)
• Symetria monokliniczna (13)
• Ortotropia (9)
• Symetria trygonalna (6)
• Symetria tetragonalna (6)
• Symetria transwersalna (cylindryczna) (5)
• Symetria kubiczna (3)
• Izotropia (2)
Dla przykładu ortotropia:
• ortotropia to lustrzane odbicie wzgl. płaszczyzn prostopadłych do osi $x_1$ , $x_2$ , $x_3$, obrót o $180^\circ$ wokół osi $x_1$ , $x_2$ , $x_3$
$$\left[\begin{array}{cccccc} C_{1111}&C_{1122}&C_{1133}& 0& 0 & 0\\ &C_{2222}&C_{2233}& 0 & 0 & 0\\ & &C_{3333}&0 &0 & 0\\ & & &C_{1212}& 0 &0 \\ & & & &C_{2323}&0\\ sym & & & & & C_{3131} \end{array}\right]$$• Izotropia - jeżeli dla dowolnego tensora ortogonalnego $\Q$ zachodzi $C_{ijkl}^{'} = C_{ijkl}$. Własności mechaniczne materiału nie zależą od kierunku (np. metale, szkło, plastik)
$$\left[\begin{array}{cccccc} C_{1111}&C_{1122}&C_{1133}& 0& 0 & 0\\ &C_{2222}&C_{2233}& 0 & 0 & 0\\ & &C_{3333}&0 &0 & 0\\ & & &C_{1212}& 0 &0 \\ & & & &C_{2323}&0\\ sym & & & & & C_{3131} \end{array}\right]$$gdzie $C_{1111} = C_{2222} = C_{3333} = C_1$, $C_{1122} = C_{1133} = C_{2233} = C_2$ oraz $C_{1212} = C_{1313} = C_{2323} = \cfrac12(C_1-C_2)$
Izotropia tensora oznacza, że jego składowe nie zależą od orientacji układu współrzędnych. Oznacza to, że tensor zachowuje się identycznie podczas każdej rotacji osi współrzędnych. Wymieńmy podstawowe tensory czwartego rzędu, które są niezmienne względem dowolnej rotacji osi współrzędnych.
$$\delta_{ij}\delta_{kl}, \quad \delta_{ik}\delta_{jl}, \quad \delta_{il}\delta_{jk}$$Te tensory bazowe spełniają warunki izotropii, co oznacza, że pozostają one niezmienione podczas dowolnej rotacji osi współrzędnych. Dlatego też, każda liniowa kombinacja tych tensorów bazowych będzie również izotropowa.
$$C_{ijkl} = \lambda_1 \delta_{ij}\delta_{kl} + \lambda_2 \delta_{ik}\delta_{jl} + \lambda_3 \delta_{il}\delta_{jk}$$Izotropowe liniowe prawo Hooke'a
Podstawiając izotropowy tensor czwartego rzędu do równania konstytutywny i wykorzystując wszystkie wspominane w tym rozdziale symetrie dostajemy
$$\sigma_{ij} = 2\mu\varepsilon_{ij} + \lambda\varepsilon_{kk}\delta_{ij}$$W zapisie macierzowym mamy
$$\left\{\begin{array}{c} \sigma_{11}\\\sigma_{22}\\\sigma_{33}\\ \sigma_{12}\\\sigma_{23}\\\sigma_{31}\end{array}\right\}= \left[\begin{array}{cccccc} \lambda+2\mu & \lambda & \lambda & 0 & 0 & 0 \\ \lambda & \lambda+2\mu & \lambda & 0 & 0 & 0 \\ \lambda & \lambda & \lambda+2\mu & 0 & 0 & 0 \\ 0 & 0 & 0 & \mu & 0 & 0 \\ 0 & 0 & 0 & 0 & \mu & 0 \\ 0 & 0 & 0 & 0 & 0 & \mu \end{array}\right] \left\{\begin{array}{c} \varepsilon_{11}\\\varepsilon_{22}\\\varepsilon_{33}\\ 2\varepsilon_{12}\\2\varepsilon_{23}\\2\varepsilon_{31}\end{array}\right\}$$a w zapisie absolutnym
$$\ss = 2\mu \ee + \lambda \tr \ee \I$$gdzie $\lambda$ oraz $\mu$ nazywamy stałymi Lamme'go (obie dodatnie!). W praktyce często używa się innych stały które łatwo można wyznaczyć przeprowadzają próbę jednoosiowego rozciągania. Stałymi tymi są
• moduł Younga
$$E = \cfrac{\mu}{\lambda+ \mu}(3\lambda +2\mu)$$• współczynnik Poissona
$$\nu = \cfrac{\lambda}{2(\lambda+\mu)}$$Naprężenie Hubera-Misesa-Henckego
Ekwiwalentne naprężenie Hubera-Misesa-Henckego (HMH)
$$\bar\sigma = \sqrt{\textstyle\frac32s_{ij}s_{ij}}\,, \qquad s_{ij} = \sigma_{ij} - \textstyle\frac13\sigma_{kk}\delta_{ij}$$Hipersprężystość izotropowa
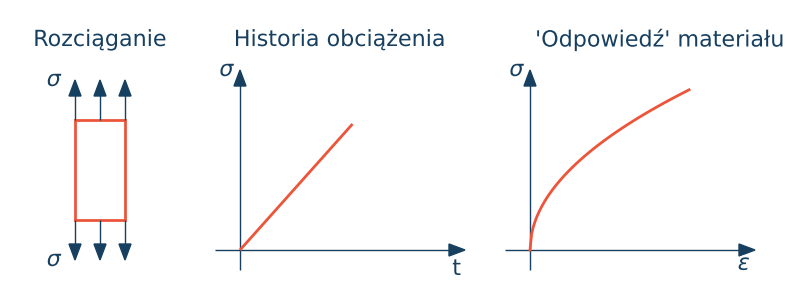
Materiałem hipersprężystym nazywamy taki materiał dla którego istnieje funkcja energii odkształcenia $U$. Równanie konstytutywne wyprowadzamy z następującego równania
$$\sigma_{ij} = \pp{U}{\varepsilon_{ij}}, \quad \ss = \pp{U}{\ee}$$Rozważać będziemy tylko materiały izotropowe czyli dla których własności materiału nie zależą od kierunku ich badania. Związek konstytutywny musi mieć taką samą postać w dowolnym ortogonalnym układzie współrzędnych, a więc musi być funkcją izotropową. Funkcja energii sprężystej musi być wyrażona za pomocą niezmienników
$$U(\ee) = U(I_1, I_2, I_3), \quad I_1 = \tr \ee, \quad I_2 = \cfrac12[(\tr \ee)^2 - \tr(\ee^2)], \quad I_3 = \det(\ee)$$Materiał NeoHookean
Funkcja energii sprężystej dla tego materiału wyrażona jest w następującej postaci
$$U = C_{10} (\bar{I_1}-3) + \cfrac{1}{D_1}(J_{el}-1)^2$$gdzie $\bar{I_1}$ oznacza pierwszy niezmiennik tensora deformacji wyznaczonego z gradientu deformacji pozbawionego części odpowiedzialnej za zmianę objętości ciała czyli $\bar{\F} = J^{-1/3}\F$
$$\bar{I_1} = tr(\bar{\C}), \quad \bar{\C} = \bar{\F}^T\bar{\F}$$a $J_{el}$ oznacza stosunek całkowitej zmiany objętości do zmiany objętości spowodowanej przez odkształcenie objętościowe związane z rozszerzalnością termiczną
$$J_{el} = \cfrac{J}{J_{th}}, \quad J_{th} = (1+\varepsilon_{th})^3, \quad J = \det \F$$Dla materiału nieściśliwego $J_{el}=1$ i powyższy wzór redukuje się do postaci
$$U = C_{10} (\bar{I_1}-3)$$Materiał zależy od dwóch stałych które oznaczają początkowy moduł ścinania i początkowy moduł objętościowy
$$\mu = 2 C_{10}, \quad K = \cfrac{2}{D_1}$$