Zasada zachowania masy

$$m = \int_{\Omega} \rho(\x,t) \,dV_t = \mathrm{const}$$

gdzie $\rho$ oznacza aktualną gęstość ośrodka ciągłego, $\Omega$ - oznacza aktualny obszar pok którym całkujemy.

Wykorzystując wzór na pochodną elementu objętości dostajemy

$$\dot{m} = \int_{\Omega} \dot{\rho}(\x,t) + \rho(\x,t)\div \v \, dV_t =0$$

Po opuszczeniu całki dostajemy lokalną postać zasady zachowania masy (równanie
ciągłości)

$$\dot{\rho} + \rho \div \v =0, \qquad \dot{\rho} + \rho v_{i,i} = 0$$

Rozpisując $\dot{\rho}$ według wzoru na pochodną materialną w opisie Eulera otrzymamy następującą postać równania ciągłości

$$\dot{\rho} + \rho v_{i,i} = \pp{\rho}{t}+\rho_{,i} v_i +\rho v_{i,i} = \pp{\rho}{t} + (\rho v_i)_{,i}$$

Zasada pędu (konfiguracja aktualna)

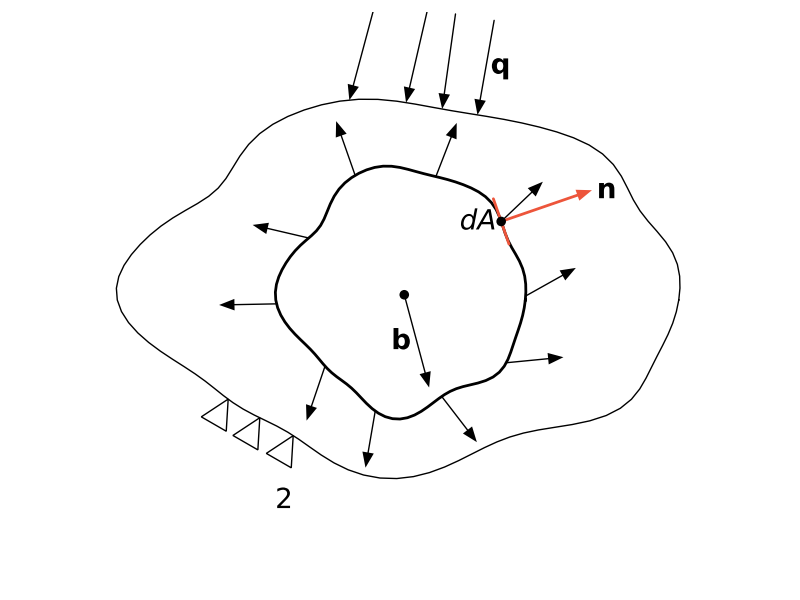
Zmiana pędu równa jest sumie sił działających na ciało

$$\dot{P} = F \Leftrightarrow \cfrac{d}{dt}\int_{\Omega_t} \rho\v \,dV_t = \int_{\Omega_t} \b \,dV_t + \int_{\dom_t}\t \, dS_t$$

Zapiszmy zasadę pędu dla dowolnego podobszaru zawierającego się w konfiguracji aktualnej. Niech będzie to obszar o objętości $\Omega$, ograniczony powierzchnią zamkniętą $\dom$. Jeżeli tak zrobimy nie musimy uwzględniać zewnętrznych sił powierzchniowych działających na brzegu ciała.

Pierwsza całka jest równa

$$\cfrac{d}{dt}\int_{\Omega_t} \rho\v \,dV = \int_{\Omega_t} \rho\dot{\v} \,dV_t = \int_{\Omega_t} \rho\a \,dV_t$$

Zapisując równanie przy użyciu notacji wskaźnikowej mamy

$$\int_{\Omega_t}\rho a_i \,dV = \int_{\Omega_t} b_i\,dV + \int_{\dom}t_i \, dS_t$$

Wykorzystując $t_i = \sigma_{ji}n_j$ dostajemy

$$\int_{\Omega_t}\rho a_i dV_t = \int_{\Omega_t}b_idV_t + \int_{\dom_t}\sigma_{ji}n_jdS_t$$

Korzystając z twierdzenia Gaussa-Ostrogradskiego, możemy zamienić całkę powierzchniową na całkę objętościową:

$$\int_{\Omega_t}\rho a_i dV_t = \int_{\Omega_t}b_idV_t + \int_{\Omega_t}\sigma_{ji,j}dV_t$$

Zamieńmy przyśpieszenie na drugą pochodną przemieszczenia i zapiszmy wszystko pod jedną całką

$$\int_{\Omega_t}(\rho \ddot{u}_i - b_i - \sigma_{ji,j})dV_t = 0$$

Ponieważ objętość $\Omega_t$ może być wybrana dowolnie, powyższe równanie będzie spełnione zawsze tylko wtedy, gdy funkcja podcałkowa będzie tożsamościowo równa 0.

$$\sigma_{ji,j} + b_i = \rho \ddot{u}_i$$

Jeśli rozważamy zagadnienia statyki, gdy pomija się udział sił bezwładności, wtedy równania te przyjmują postać:

$$\sigma_{ji,j} + b_i = 0$$

Sprawę możemy jeszcze bardzie uprościć pomijając siły objętościowe.

$$\sigma_{ji,j} = 0$$

Zasada krętu (konfiguracja aktualna)

Zmiana krętu równa jest sumie momentów działających na ciało względem dowolnego punktu $0$.

$$\dot{K}_0 = M_0 \Leftrightarrow \cfrac{d}{dt}\int_{\Omega_t} \rho\v \times \x \,dV = \int_{\Omega_t} \b \times \x \,dV + \int_{\dom}\t \times \x \, dS_t$$

Przekształćmy pierwszą całkę wykorzystując wzór na pochodną zdefiniowaną na konfiguracji aktualnej

$$\cfrac{d}{dt}\int_{\Omega_t} \rho \epsilon_{ijk} v_i x_j \,dV= \int_{\Omega_t} \dot{\overline{\epsilon_{ijk}v_ix_j}} + v_{m,m}(\rho\epsilon_{ijk}v_ix_j) dV_t$$

Wykorzystajmy wzór na pochodną iloczynu funkcji

$$\int_{\Omega_t}[\dot{\rho}\epsilon_{ijk}v_ix_j + \rho \epsilon_{ijk} \dot{v_i}x_j + \rho \epsilon_{ijk} v_i \dot{x_j} + v_{m,m}(\rho\epsilon_{ijk}v_ix_j)] dV_t = \int_{\Omega_t} \epsilon_{ijk} \rho \dot{v}_ix_j \,dV_t$$

W powyższym wzorze następujące człony są równe zero, ze względu na nasuwanie tensora symetrycznego na antysymetryczny oraz z równania ciągłości

$$\epsilon_{ijk} \rho \dot{x}_i v_j =\epsilon_{ijk} \rho v_i v_j = 0, \quad \epsilon_{ijk}v_ix_j(\dot{\rho} + v_{m,m}\rho) = 0$$

Druga całka przy wykorzystaniu twierdzenia Cauchy oraz tweirdzenia Gausa-Ostrogradzkiego jest następująca

$$\int_{\dom_t}\epsilon_{ijk} t_i x_j \, dS_t = \int_{\dom_t}\epsilon_{ijk} \sigma_{li} n_l x_j \, dS_t = \int_{\Omega_t}\left(\epsilon_{ijk} \sigma_{li}x_j\right)_{,l} \, dV_t$$

Zajmijmy się teraz funkcją podcałkową:

$$\left(\epsilon_{ijk} \sigma_{li}x_j\right)_{,l} = \epsilon_{ijk}\left( \sigma_{li}x_j\right)_{l} = \epsilon_{ijk}\left(\sigma_{li,l}x_j + \sigma_{li}x_{j,l}\right) = \epsilon_{ijk}\left(\sigma_{li,l}x_j + \sigma_{li}\delta_{jl}\right) = \epsilon_{ijk}\left(\sigma_{li,l}x_j + \sigma_{ji}\right)$$

Przepiszmy jeszcze raz równanie krętu

$$\int_{\Omega_t} \epsilon_{ijk} \rho\dot{v_i}x_j \,dV = \int_{\Omega_t} \epsilon_{ijk} b_i x_j \,dV + \int_{\Omega_t} \epsilon_{ijk}\left(\sigma_{il,l}x_j+ \sigma_{ij}\right)\,dV_t$$

Sprowadźmy wszystko pod jedną całkę oraz pogrupujmy wyrazy w następujący sposób.

$$\int_{\Omega_t} \epsilon_{ijk}x_j\left( \rho\dot{v_i}-\sigma_{li,l} - b_i\right) +\epsilon_{ijk}\sigma_{ji} \, dV_t = 0$$

Wykorzystując zasadę zachowania pędu możemy wyzerować jeden z członów. Ostatecznie dostajemy że

$$\epsilon_{ijk}\sigma_{ji} = 0\Leftrightarrow \ss = \ss^T.$$

Oznacza to, że zastosowanie zasady zachowania momentu pędu dla ciała odkształcalnego prowadzi do symetrii tensora naprężenia.