Siły
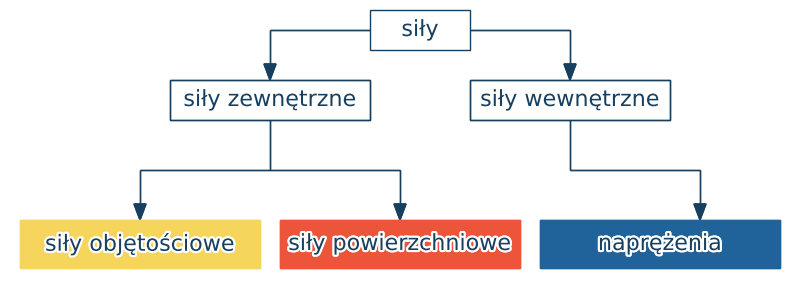
W mechanice ośrodków ciągłych wyróżniamy następujące rodzaje sił:
• siły zewnętrzne – oddziaływanie otoczenia na cząstki należące do ciała
1) objętościowe
2) powierzchniowe
• siły wewnętrzne – oddziaływanie cząstek ciała na siebie wzajemnie.
Wyróżniać będziemy następujące rodzaje sił zewnętrznych:
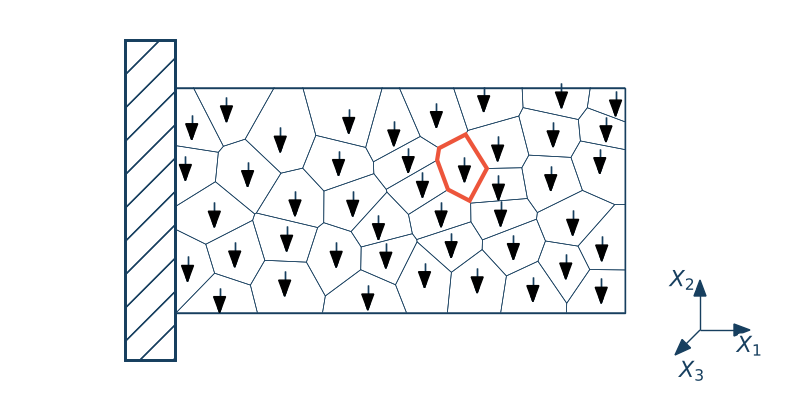
• Zewnętrzne siły objętościowe - reprezentują one oddziaływanie otoczenia na punkty wewnątrz ciała. Siłami takimi są np. grawitacja lub oddziaływania elektromagnetyczne
Jednostką gęstości sił objętościowych jest $[\q] = \mathrm{N}/\mathrm{m}^3$. W przypadku siły grawitacji możemy zapisać
$$\b(\x, t) = \rho \g$$W tym przypadku siły objętościowe nie będą zależały od czasu i punktu.
• Zewnętrzne siły powierzchniowe - reprezentują one oddziaływanie otoczenia na punkty materialne znajdujące się na powierzchni zewnętrznej ciała. Siły tego rodzaju nie oddziałują bezpośrednio na punktu wewnątrz ciała
$$\q(\x, t) = \lim_{\Delta A\ \rightarrow 0}\cfrac{\Delta\f}{\Delta A} = \cfrac{d\f}{dA}, \quad d\f = \q(\x, t) dA .$$Jednostką gęstości sił powierzchniowych jest $[\q] = \mathrm{N}/\mathrm{m}^2= \mathrm{Pa}$.Przykłady takich sił to ciśnienie hydrostatyczne wody na konstrukcję, siły tarcia podczas kontaktu dwóch ciał.
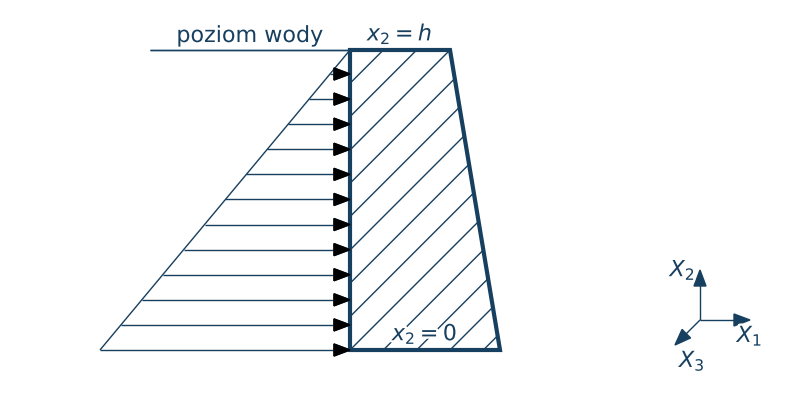
Rozkład sił powierzchniowych możemy opisać następującym równaniem
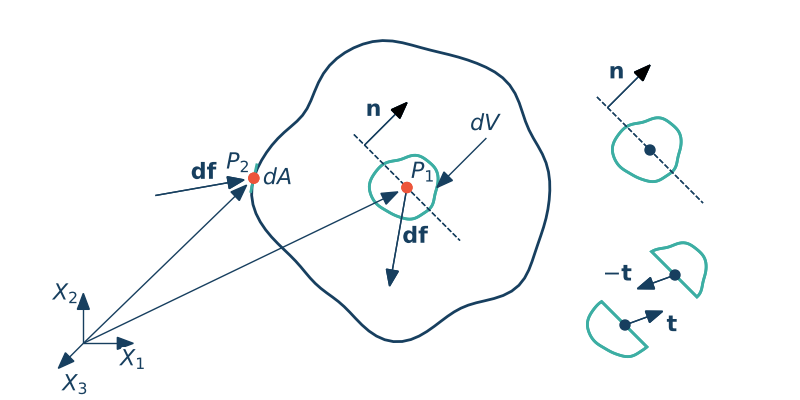
$$\q(\x) = \vr{\rho g (h-x_2)}{0}{0}$$• Siły wewnętrzne. Zakładamy istnienie sił wewnętrznych – przekonuje nas o tym fakt, że cząstki wewnątrz ciała poruszają się (zachodzi odkształcenie ciała), z reguły każda w nieco inny sposób. Rozkład sił wewnętrznych opisany zatem będzie za pomocą wektorowej funkcji gęstości wewnętrznych sił powierzchniowych $\t(\x ,\n , t)$
$$\t(\x, \n, t) = \lim_{\Delta A\ \rightarrow 0}\cfrac{\Delta\f}{\Delta A} = \cfrac{d\f}{dA}$$Funkcja gęstości wewnętrznych sił powierzchniowych jest polem wektorowym. Wektor ten nazywać będziemy wektorem naprężenia w danym punkcie przy cięciu powierzchnią o normalnej $\n$. Wektor naprężenia $\t$ jest przyporządkowany elementowi $dS$ o konkretnej normalnej $\n$.
Tensor naprężenia Cauchy

Na ścianach sześcianu działają wektory naprężenia o współrzędnych
$$\t_1 = \sigma_{11} \e_1 + \sigma_{12} \e_2 + \sigma_{13} \e_3$$ $$\t_2 = \sigma_{21} \e_1 + \sigma_{22} \e_2 + \sigma_{23} \e_3$$ $$\t_3 = \sigma_{31} \e_1 + \sigma_{32} \e_2 + \sigma_{33} \e_3$$Powyższe równania możemy zapisać używając konwencji sumacyjnej jako
$$\t_i = \sigma_{ij}\e_j$$gdzie $\sigma_{ik} = \t_i \e_k$, bez pogrubienia, normalna macierz współczynników.
Twierdzenie Cauchy Zależność między wektorem naprężenia $\t(\n)$ a normalną $\n$ do powierzchni, na jakiej ten wektor działa jest liniowa. Tensorem, który to odwzorowanie liniowe opisuje, jest tensor
$$\t(\n) = \ss^T\n, \qquad t_i = \sigma_{ji} n_j$$gdzie $\ss$ nazywamy tensorem naprężenia.
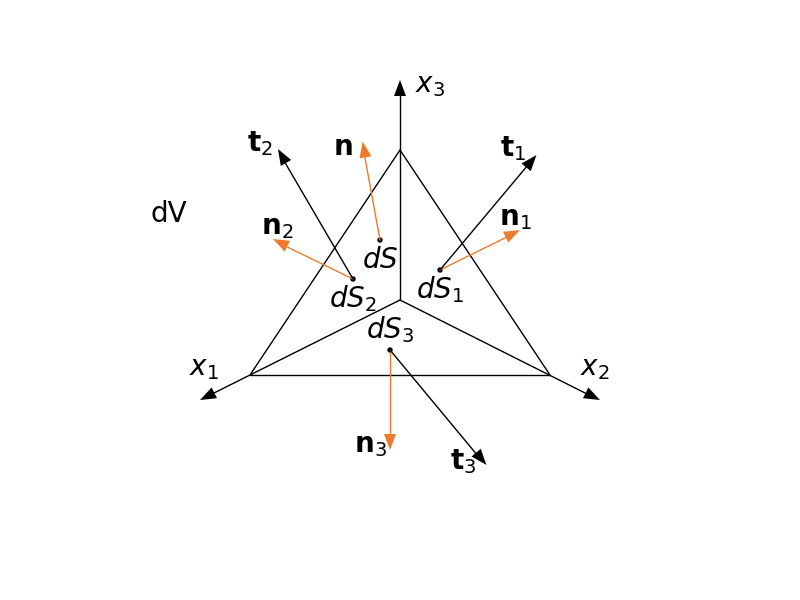
Znakowanie naprężenia. Jeżeli wektor naprężenia działa na powierzchni o normalne która jest zgodna z zwrotami układu współrzędnych to dajemy wtedy plus. W myśl tej zasady możemy zapisać równanie równowagi dla czworościanu. Płaszczyzna o normalnej $\n$ jest dowolna. Wszystkie siły działające na czworościan muszą być w równowadze a więc
$$-\t_1\mathrm{d}S_1 -\t_2\mathrm{d}S_2 - \t_3\mathrm{d}S_3 + \t \mathrm{d}S + \b dV = 0$$Objętość czworościanu możemy wyznaczyć jako
$$dV = \cfrac{1}{3}h_1dS_1 = \cfrac{1}{3}h_2dS_2 = \cfrac{1}{3}h_3dS_3 = \cfrac{1}{3}hdS$$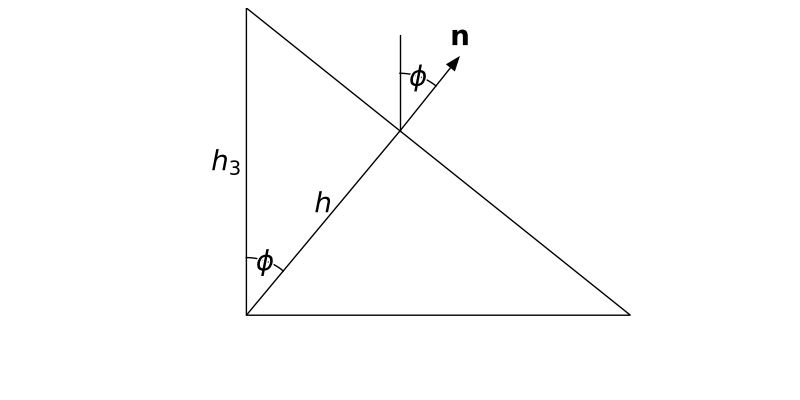
W czworościanie możemy wyróżnić 4 wysokości. Każda z nich poprowadzona jest z innego wierzchołka. Związek miedzy wysokościami jest następujący
$$\cfrac{h}{h_1} = \cos \phi = \n\cdot\e_1, \qquad \cfrac{h}{h_2} = \cos \phi = \n\cdot\e_2, \qquad \cfrac{h}{h_3} = \cos \phi = \n\cdot\e_3$$gdzie $\phi$ oznacza kąt między normalną $\n$ a wersorem $\e_3$. Korzystając z powyższych zależności możemy wyrazić pole powierzchni $dS_i$ przez pole powierzchni $dS$.
$$h_1dS_1 = hdS \quad \rightarrow \quad dS_1 = \cfrac{h}{h_1} dS = (\n\cdot\e_1) dS$$Podstawiając do równania równowagi dostajemy
$$-\t_1(\n\cdot\e_1) dS -\t_2(\n\cdot\e_1) dS - \t_3(\n\cdot\e_1) dS + \t \mathrm{d}S + \b \cfrac{1}{3}hdS = 0.$$Jeżeli czworościan będzie się coraz bardziej kurczył to wtedy $ V \rightarrow 0, \quad h \rightarrow 0$, a więc możemy pominąć człon od sił objętościowych. Po podzieleniu przez $dS$ dostajemy
$$-\t_1(\n\cdot\e_1) -\t_2(\n\cdot\e_1) - \t_3(\n\cdot\e_1) + \t = 0$$Korzystając z konwencji sumacyjnej dostajemy
$$\t = \t_i(\n \cdot \e_i)$$Podstawmy to do naszego równania $\t_i = \sigma_{ij} \e_j$ (równanie to zostało wyprowadzone wcześniej)
$$\t = \sigma_{ij} \e_j(\n \cdot \e_i) = (\sigma_{ij}\e_j\otimes\e_i)\cdot \n = \ss^T \cdot \n$$Definicja tensora naprężenia w różnych konfiguracjach
Wprowadżmy pojęcie nominalnego wektora naprężenia $\t_R$ który jest zdefiniowany w taki sposób aby
$$\t dA_t = \t_r dA_0$$czyli chcemay aby wektory $\t$ i $\t_r$ miały ten sam kierunek ale w ogólności inną długość.
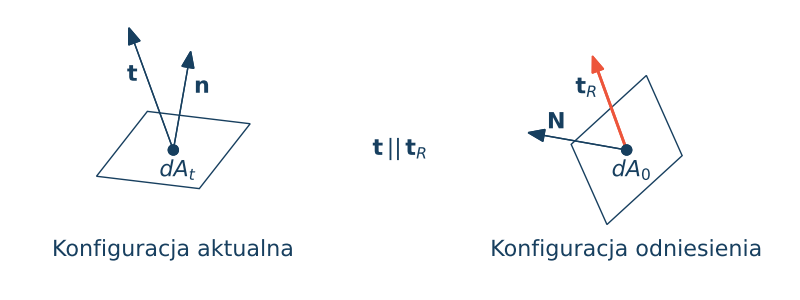
Zapiszmy wektor naprężenia w konfiguracji aktualnej za pomocą tensora naprężenia
$$\ss \n dA_t = \t_R dA_0$$Wykorzystując wyprowadzony już wcześniej wzór na zmianę powierzchni mamy, że
$$J \ss \, \F^{-T}\N dA_0 = \t_R dA_0$$Powyższa równność musi być spełniona dla każdego $dA_0$ a więc
$$\t_R = J \ss \, \F^{-T}\N$$Zdefinujmy w tym miejscu nowy tensor naprężenia $\T$ który podobnie jak tensor Cauchego będzie spełniał następującą równość
$$\t_R = \T \N$$Wykorzystując wprowadzoną nową miarę naprężenia dostajemy
$$\T \N = J \ss \, \F^{-T}\N$$czyli dla dowolnego $\N$ musi zachodzić że
$$\T = J \ss \, \F^{-T}$$Tensor $\T$ nazywamy tenosrem Pioli-Kirchohoffa pierwszego rodzaju. Jest to tensor niesymetryczny!