Odkształcenie objętościowe
W konfiguracji początkowej ciała wybierzmy elementarny prostopadłościan o objętości $dV_0$, który w konfiguracji aktualnej (zdeformowanej) będzie elementarnym graniastosłupem o objętości $dV_t$ %\cite{paluch}.
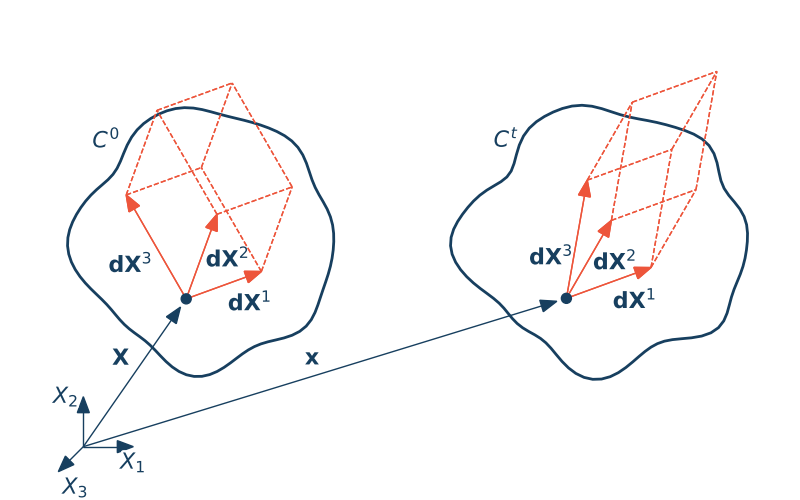
W konfiguracji aktualnej objętość ta będzie wynosić odpowiednio
$$dV_t = d\x^1 \left(d\x^2 \times d\x^3\right) = \epsilon_{ijk}dx^1_i dx^2_j dx^3_k$$Wykorzystując definicję gradientu deformacji
$$dx^1_i = \cfrac{\partial x^1_i}{\partial X^1_l} dX^1_l, \qquad dx^2_j = \cfrac{\partial x^2_j}{\partial X^2_m} dX^2_m, \qquad dx^3_k = \cfrac{\partial x^3_k}{\partial X^2_n} dX^3_n$$Podstawmy powyższe wzory do równania na aktualną objętość
$$dV_t = \epsilon_{ijk}F_{il}dX^1_lF_{jm}dX^2_mF_{kn}dX^3_n = \det \F \epsilon_{lmn} dX_l dX_m dX_n = JdV_0$$Przy wyprowadzaniu wzoru skorzystaliśmy z następującej tożsamości
$$\epsilon_{ijk}A_{il}A_{jm}A_{kn} = \epsilon_{lmn}\det[A_{pq}] \quad\mbox{(dla dowolnej macierzy $[A_{pq}]$)}$$O zmianie objętości w danym punkcie ciała odkształcalnego decyduje wyznacznik gradientu deformacji (jakobian).
Odkształcenie powierzchniowe
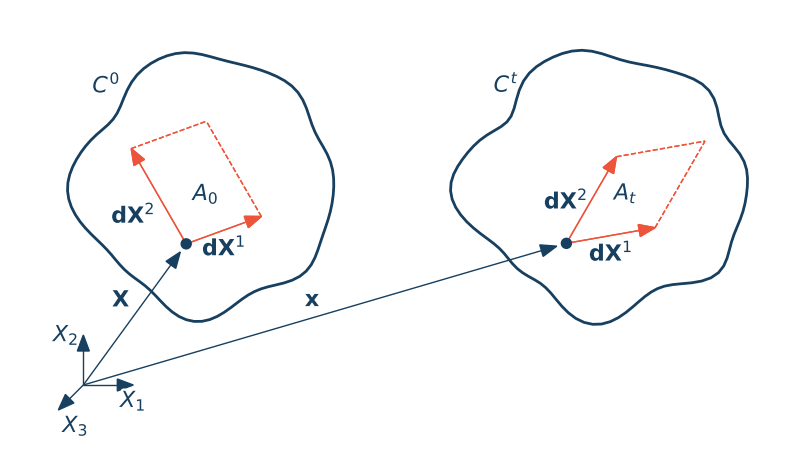
Pole powierzchni w konfiguracji początkowej
$$dA_0 \N = d \X^1 \times d \X^2 ,\qquad dA_0 N_k = dX^1_i dX^2_j \epsilon_{ijk},$$Pole powierzchni w konfiguracji aktualnej
$$dA_t\n = d \x^1\times d\x^2, \qquad dA_tn_k = dx^1_i dx^2_j \epsilon_{ijk},$$ $$d A_tn_k = F_{il}dX^1_l\,F_{jm}dX^2_m\,\epsilon_{ijk} = dX^1_l dX^2_m\,F_{il}F_{jm}\delta_{nk}\,\epsilon_{ijn} = dX^1_l dX^2_m\,F_{il}F_{jm}F_{np}F^{-1}_{pk}\,\epsilon_{ijn}$$ $$dX^1_l dX^2_m\epsilon_{lmp}\,\det\F\,F^{-1}_{pk} = dA_0N_p\,JF^{-1}_{pk}$$ $$dA_t\n = J\F^{-T} dA_0\N,$$Symbol $(\cdot)^{-T}$ oznacza transpozycję i odwrotność tensora $(\cdot)$.
Powyższy wzór nosi często nazwę wzoru Nansona. Jest to równanie wektorowe które wiąże ze sobą pole powierzchni i wektor normalny w konfiguracji odniesienie i konfiguracji zdeformowanej.