Związki geometryczne

Wykorzystując związek między $\F$ i $\H$ dla miar deformacji otrzymujemy następujące związki w opisie materialnym i przestrzennym

$$\C = \F^T\F = (\H+\I)^T(\H+\I) = \H + \H^T + \H^T\H + \I$$ $$\c = \f^T\f = (\I-\h)^T(\I-\h) = -\h - \h^T + \h^T\h + \I$$

W zapisie indeksowym wzory te wyrażają się następująco

$$C_{ij} = H_{ki}H_{kj} + H_{ij} + H_{ji} +\delta_{ij}$$ $$c_{ij} = - h_{ij} - h_{ji} + h_{ki}h_{kj} + \delta_{ij}$$

Wykorzystując tak obliczone tensory deformacji możemy zapisać tensor Greena $\E$ i Almansiego $\e$ jako

$$\e = \cfrac{1}{2}(\h + \h^T - \h^T\h)$$

Tensor małego odkształcenia - symetryczna część gradientu przemieszczenia

Tensor małego (liniowego) obrotu - antysymetyrczna cześć gradientu przemieszczenia

$$\mathbf{\omega} = \cfrac{1}{2}(\H - \H^T) \approx \cfrac{1}{2}(\h - \h^T)$$

Interpretacja składowych miar deformacji

• składowe normalne (składowe które leżą na przekątnej głównej tensora drugiego rzędu)

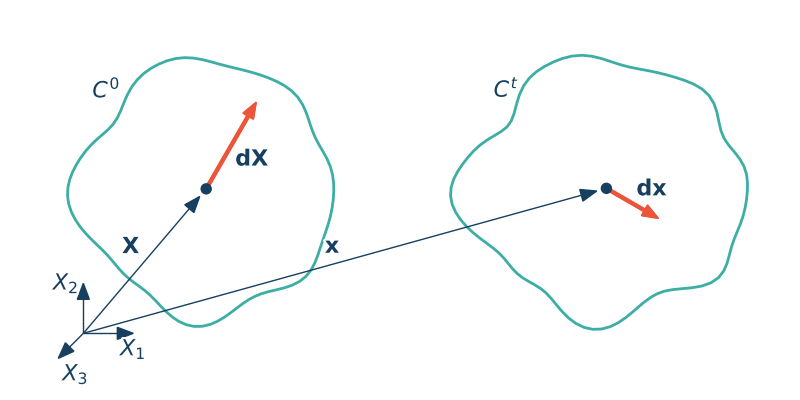
Rozważmy dwie konfigurajce ciała $C_0$ i $C_t$. Wybierzy dowolny punkt materialny $\X$ oraz infinitezymalne włókno materialne $d\X$. W konfiguracji aktualnej włókno ulega deformacji, (zmienia się jego długość oraz orientacja). Oznaczmy zdeformowane włókno jako $d\x$.

Wybierzmy włókno materialne $d\X$ w konfiguracji odniesienia oraz jego transformację w konfiguracji aktualnej $d\x$ tak aby jego kierunek był równy

$$\mathrm{d}\X = \mathrm{dL}\N, \qquad \mathrm{d}\x = \mathrm{dl}\n, \qquad |\N| = 1, \, |\n| = 1$$

Wykorzystując definicję tensora deformacji $C$ kwadrat długości tego włókna wynosi

$$\mathrm{dl}^{2} = \mathrm{d}\X\C\mathrm{d}\X= \mathrm{dL}^{2} \N\C\N$$

Wprowadźmy następującą definicję $\lambda = \cfrac{\mathrm{dl}}{\mathrm{dL}}$ wtedy

$$\lambda^{2} = \N\C\N$$

Podstawmy za $\N=\e_1 \quad \Rightarrow \quad \lambda_1^{2} = \e_1 \C\e_1 = C_{11}$. Podobnie podstawiając pozostałe wektory bazowe dostajemy $\lambda_2^{2} = \e_2 \C\e_2 = C_{22}$ oraz $\lambda_3^{2} = \e_3 \C\e_3 = C_{33}$

$$\left[\begin{array}{ccc}1 & 0 & 0\\\end{array}\right] \left[ \begin{array}{ccc} C_{11} & C_{12} & C_{13}\\ & C_{22} & C_{23}\\ sym & & C_{33} \end{array}\right] \left[\begin{array}{c}1\\0\\0\\\end{array}\right]=C_{11}$$

Składowe normalne tensora deformacji $\C$ są równe kwadratowi względnego rozciągnięcia włókien materialnych wzdłuż kierunków wyznaczonych przez wektory bazowe.

Jeżeli włókno nie uległo deformacji to składowe normalne są równe $1$. Maksymalne wydłużenia względne otrzymujemy dla włókien wzdłuż kierunków głównych $\C$.

• składowe styczne

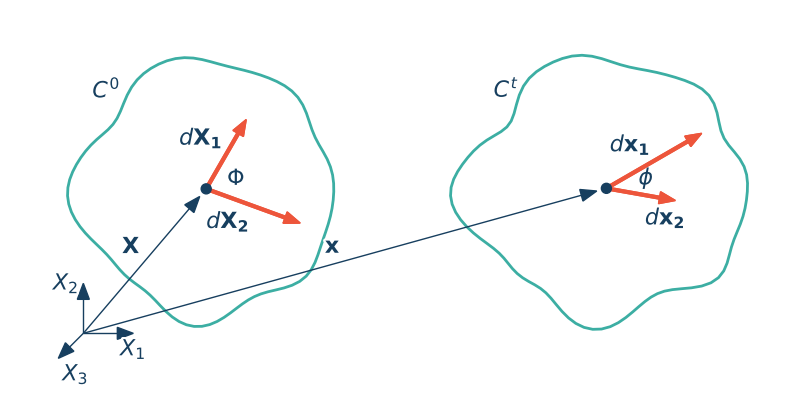
Rozważmy dwie konfigurajce ciała $C_0$ i $C_t$. Wybierzy dowolny punkt materialny oraz dwa włókna materialne $d\X_1$ oraz $d\X_2$. Kąt między tymi włóknami wynosi $\Phi$. W konfiguracji aktualnej włókna ulegają deformacji. Oznaczmy je odpowiednio $d\x_1$ oraz $d\x_2$. Kąt między zdeformowanymi włóknami wynosi $\phi$.

Wybierzmy dwa włókna materialne $d\X_1$ i $d\X_{2}$ w konfiguracji odniesienia oraz ich transformację w konfiguracji aktualnej $d\x_{1}$ i $\mathrm{d}\x_{2}$ tak aby

$$\mathrm{d}\X^{1} = \mathrm{dL_{1}}\N_{1}, \qquad \mathrm{d}\x_{1} = \mathrm{dl_{1}}\n_{1}, \qquad |\N_{1}| = 1, \, |\n_{1}| = 1$$ $$\mathrm{d}\X_{2} = \mathrm{dL_{2}}\N_{2}, \qquad \mathrm{d}\x_{2} = \mathrm{dl_{2}}\n_{2}, \qquad |\N_{2}| = 1, \, |\n_{2}| = 1$$

Obliczmy cosinus kąta między włóknami w konfiguracji początkowej i aktualnej. Wykorzystując wektory jednostkowe kąt ten w konfiguracji początkowej wynosi

$$\cos(\Phi) = \N_{1}\N_{2},$$

natomiast w konfiguracji aktualnej wykorzystując definicję tensora deformacji dostajemy

$$\cos(\phi) = \n_{1}\n_{2} = \cfrac{1}{\mathrm{dl}_{1}\mathrm{dl}_{2}}\mathrm{d}\x_{1} \mathrm{d}\x_{2} = \cfrac{1}{\mathrm{dl}_{1}\mathrm{dl}_{2}}(\F \mathrm{d}\X_{1}) (\F \mathrm{d}\X_{2}) =$$ $$\cfrac{\mathrm{dL}_{1}\mathrm{dL}_{2}}{\mathrm{dl}_{1}\mathrm{dl}_{2}}(\F \N_{1}) (\F \N_{2}) = \cfrac{1}{\lambda_{1} \lambda_{2}} \N_{1}\C\N_{2}.$$

Zmianę kąta między włóknami w wyniku deformacji (kąt odkształcenia postaciowego) możemy zapisać jako

$$\gamma = \Phi - \phi$$

Podstawmy za $\N_{1}=\e_1,\ \N_{2} = \e_2$ wtedy

$$\cos(\Phi) = \e_1\e_2=0 \rightarrow \Phi=\cfrac{\pi}{2}, \,\, \cos(\phi) = \cfrac{1}{\lambda_{1} \lambda_{2}} \e_1\C\e_2 = \cfrac{C_{12}}{\sqrt{C_{11}}\sqrt{C_{22}}}$$

Policzmy sinus kąta $\gamma$: $\sin(\gamma) = \sin(\pi/2 - \phi) = \cos(\phi)$

Ostatecznie dostajemy

$$\sin(\gamma_{12}) = \cfrac{C_{12}}{\sqrt{C_{11}}\sqrt{C_{22}}}$$

W powyższym wzorze dodaliśmy index $12$ aby podkreślić że ten kąt jest między włóknami $1$ i $2$. Identyczne kalkulacje możemy przeprowadzić dla pozostałych kombinacji wektorów bazowych. Zależność tą możemy przekształcić do następującej postaci

$$C_{12} = \sin(\gamma_{12}) \lambda_1 \lambda_2$$ $$C_{13} = \sin(\gamma_{13}) \lambda_1 \lambda_3$$ $$C_{23} = \sin(\gamma_{23}) \lambda_2 \lambda_3$$

Składowe styczne tensora deformacji $\C$ są równe sinusowi kąta odkształcenia postaciowego między włóknami materialnym pomnożonymi przez względne rozciągnięcie tych włókien.

Jeżeli kąt pomiędzy włóknami nie zmienił się podczas deformacji, to $\sin(\gamma)=0$.

Tensor odkształcenia Greena

Zdefiniujmy przyrost długości włókna materialnego jako

$$\lambda = \cfrac{dl}{dL}, \qquad dl = dL + du = (dL + du)/dL \cdot dL = \left(\cfrac{dL}{dL} + \cfrac{du}{dL}\right)dL = (1+\varepsilon)dL \rightarrow \lambda =\varepsilon+1$$

• składowe normalne

$$E_{11} = \cfrac{1}{2}(C_{11}-1) = \cfrac{1}{2}(\lambda_1^{2}-1) =\cfrac{1}{2}(\varepsilon_1^{2}+2\varepsilon_1)\approx \varepsilon_1$$ $$E_{22} = \cfrac{1}{2}(C_{22}-1) = \cfrac{1}{2}(\lambda_2^{2}-1) =\cfrac{1}{2}(\varepsilon_2^{2}+2\varepsilon_2)\approx \varepsilon_2$$ $$E_{33} = \cfrac{1}{2}(C_{33}-1) = \cfrac{1}{2}(\lambda_3^{2}-1) =\cfrac{1}{2}(\varepsilon_3^{2}+2\varepsilon_3)\approx \varepsilon_3$$

• składowe styczne

Wykorzystując przybliżenie dla małych katów $\sin(\alpha) \approx \alpha$.

$$E_{12} = \cfrac{1}{2}C_{12} = \cfrac{1}{2}\sin(\gamma_{12}) \lambda_1 \lambda_2 = \cfrac{1}{2}\gamma_{12}(1+\varepsilon_1)(1+\varepsilon_2) = \cfrac{1}{2}\gamma_{12}(1 +\varepsilon_1+\varepsilon_2+\varepsilon_1\varepsilon_2) \approx \cfrac{1}{2}\gamma_{12}$$ $$E_{13} = \cfrac{1}{2}C_{13}\approx \cfrac{1}{2}\gamma_{13}$$ $$E_{23} = \cfrac{1}{2}C_{23}\approx \cfrac{1}{2}\gamma_{23}$$

W powyższych wzorach pominęliśmy wszystkie nieliniowe człony $\gamma\varepsilon$.

Linearyzacja tensora Greena prowadzi do odkształceń poza przekątną główną równych połowie wartości kąta odkształcenia postaciowego.

Warunki nierozdzielności odkształceń

Znając ciągłą funkcję pola przemieszczenia $\u(\X,t)$ jesteśmy zawsze w stanie znaleźć odpowiadające temu polu pole odkształcenia. Dla przykładu, tensora Greena otrzymujemy poprzez obliczanie odpowiednich gradientów przemieszczenia

$$E_{ij} = \cfrac12(u_{i,j} + u_{j,i} + u_{k,i} u_{k,j}).$$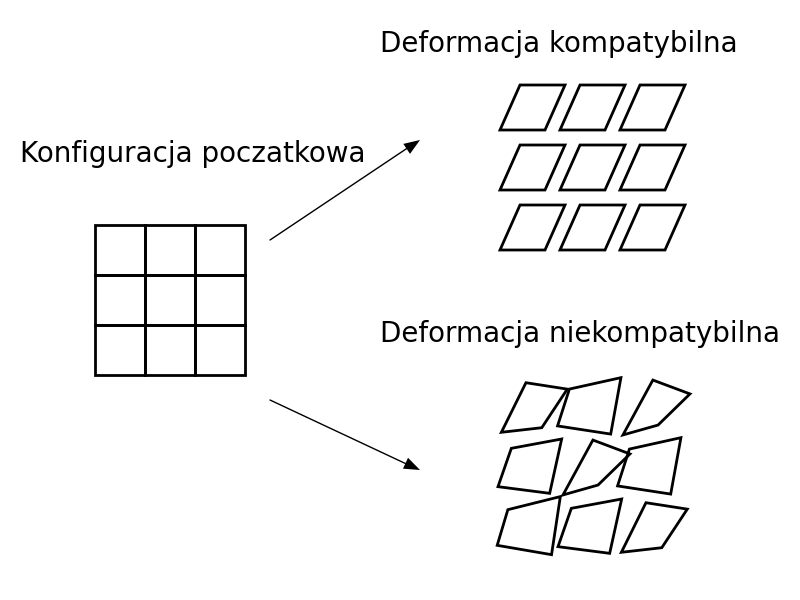

Warunkami nierozdzielności dla tensora drugiego rzędu nazywamy warunki jakie musi on spełnić aby być tensorem odkształcenia, czyli aby istniało pole przemieszczenie z którego jest on wyliczany.

Potencjalne pole wektorowe

$$T(\x), \quad \g(\x) = \pp{T(\x)}{\x}$$

Zadajmy sobie teraz pytanie. Jeżeli znamy pole $\g(\x)$ jak znaleźć pole $T(\x)$. Możemy to zapisać jako

$$g_{x_1} - \pp{T(\x)}{x_1} = 0, \quad g_{x_2} - \pp{T(\x)}{x_2}= 0, \quad g_{x_3} - \pp{T(\x)}{x_3} = 0$$

Powyższy układ równań różniczkowych jest nadokreślony. Obliczmy gradient z pola $g(x)$ oraz z pola $T(x)$

$$\g \otimes \nabla = (\nabla T) \otimes \nabla$$

Rozpisują powyższy układ dostajemy 9 równań

$$\pp{g_1}{x_1} = \cfrac{\partial^2 T}{\partial x_1^2}, \quad \pp{g_1}{x_2} = \cfrac{\partial^2 T}{\partial x_1 \partial x_2}, \quad \pp{g_1}{x_3} = \cfrac{\partial^2 T}{\partial x_1, \partial x_3}$$ $$\pp{g_2}{x_1} = \cfrac{\partial^2 T}{\partial x_2 \partial x_1}, \quad \pp{g_2}{x_2} = \cfrac{\partial^2 T}{\partial x_2^2}, \quad \pp{g_2}{x_3} = \cfrac{\partial^2 T}{\partial x_2, \partial x_3},$$ $$\pp{g_3}{x_1} = \cfrac{\partial^2 T}{\partial x_3 \partial x_1}, \quad \pp{g_3}{x_2} = \cfrac{\partial^2 T}{\partial x_3\partial x_2}, \quad \pp{g_3}{x_3} = \cfrac{\partial^2 T}{\partial x_3^2, }$$

Wykorzystując fakt, że kolejność różniczkowania nie ma znaczenia dostajemy

$$\pp{g_1}{x_2} - \pp{g_2}{x_1}=0, \quad \pp{g_1}{x_3} - \pp{g_3}{x_1}=0, \quad \pp{g_2}{x_3} - \pp{g_3}{x_2}=0$$

Powyższe równania możemy zapisać jako

$$\rot \g = \mathbf{0}, \quad \pp{g_i}{x_j} - \pp{g_j}{x_i}=0$$

Analogiczne rozumowanie możemy zastosować do poszukiwania równań ruchu $\x = \phi(\X)$ bazując na znanym gradiencie deformacji czyli

$$\F = \boldsymbol \phi(\X) \otimes \nabla_{X} \to \F \otimes \nabla_{X} = (\boldsymbol \phi(\X) \otimes \nabla_{X})\otimes \nabla_{X}$$

Rozpisując powyższe równanie tensorowe dostajemy układ 18 równań. Dla przykładu rozpiszmy jedno z nich

$$\pp{F_{11}}{X_1} = \pp{^2\phi_1}{X_1 \partial X_1}$$

Wykorzystując jak poprzednio fakt, że kolejność różniczkowania nie ma znaczenia dostajemy

$$\rot \F = \boldsymbol 0, \quad \nabla_{X} \times \F = \boldsymbol 0, \quad \epsilon_{kip}F_{ij,k} = 0$$