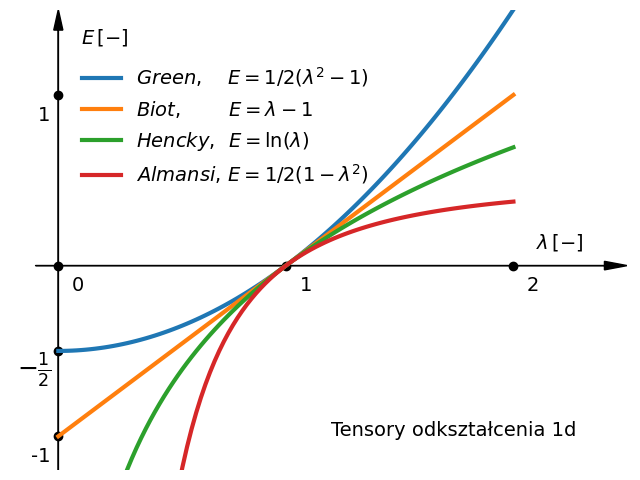Ciało odkształcalne - kontinuum materialne, ośrodek ciągły
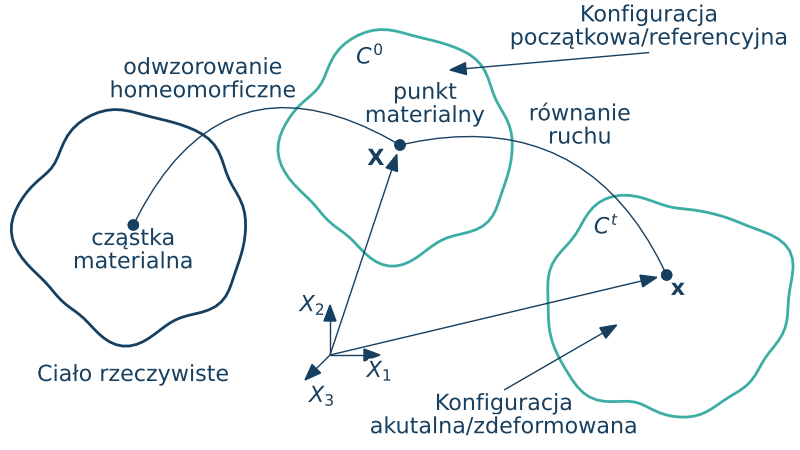
Definicja ciała jako obszaru w przestrzeni punktowej w danej chwili ruchu
• różne konfiguracje ciała $C^t$ związane z chwilami czasowymi $t$ (w tym m.in. $C^0$ i $C^t$)
• konfiguracji odniesienia $C^r$ w której punkty materialne zostaną zdefiniowane przez ich współrzędne $\X$. Tą konfigurację będziemy utożsamiać z konfiguracją $C^0$.
• aktualne położenie punktu materialnego w konfiguracji zdeformowanej $C^t$ oznaczać będziemy przez $\x$
Opis materialny
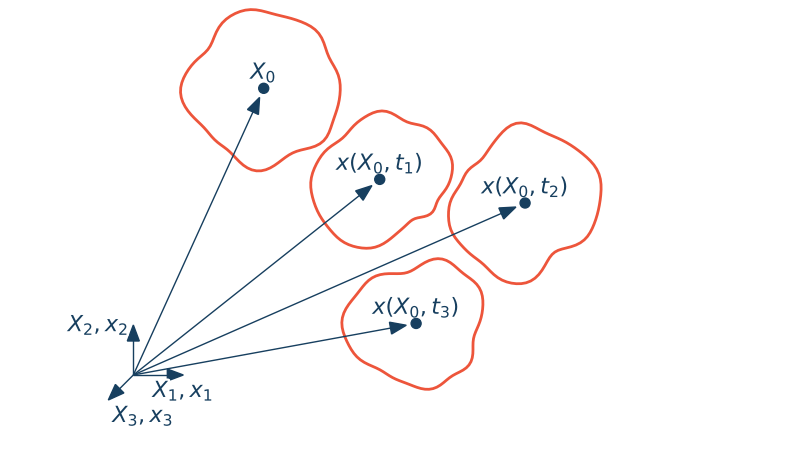
Opis materialny nazywany jest również opisem Lagrange'a. Ruch ciała interpretujemy jako transformację współrzędnych punktów materialnych $\X$ z uwzględnieniem czasu do ich aktualnego położenia $\x$ .
$$\x = \x(\X,t), \quad x_i = x_i(X_j,t)$$W opisie materialnym stawiamy pytanie w jakim punkcie przestrzeni $\x$ znajduje się cząstka, która na początku ruchu, znajdowała się w punkcie $\X$. Można powiedzieć, że punkt o współrzędnych $\X$ to "id" cząstki materialnej. Opis materialny polega na zdefiniowaniu zbioru punktów materialnych które podążają za deformacją ciała. Punkty materialne są niejako "przyspawane" do cząsteczek materialnych i podążają za nimi.
Przykłady:
• ruch sztywny:
• wydłużenie w kierunku $x_1$:
$$x_1 = X_1 + \alpha(t)\, X_1, \quad x_2 = X_2, \quad x_3 = X_3$$
• ścinanie w płaszczyźnie ($x_1,x_2$):
$$x_1 = X_1 + \alpha(t)\, X_2, \quad x_2 = X_2, \quad x_3 = X_3$$
Opis przestrzenny
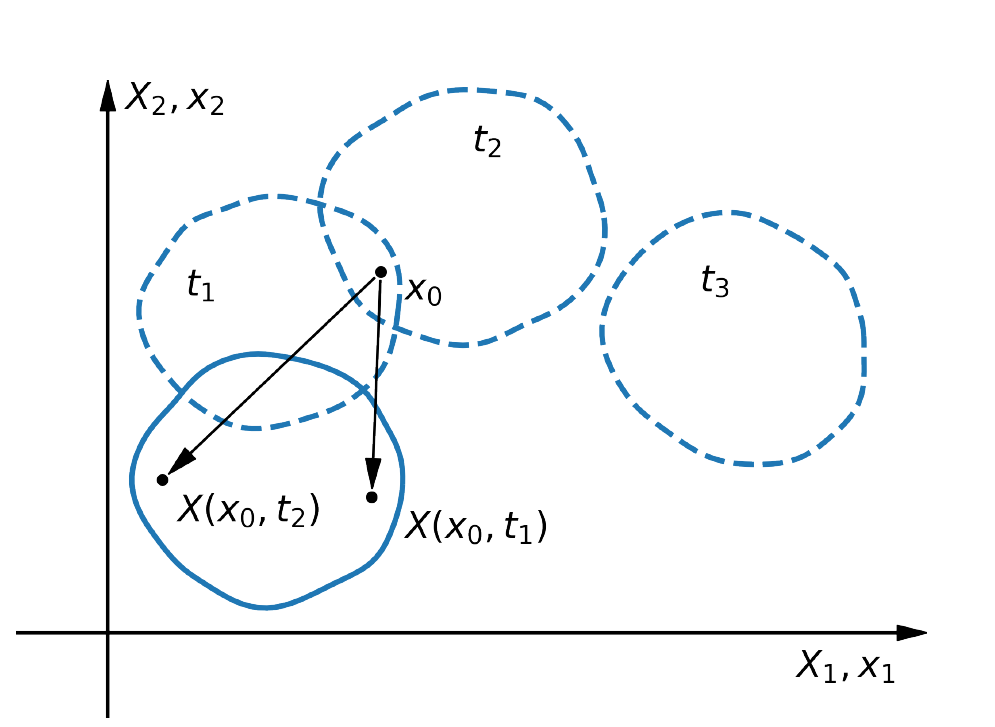
Opis przestrzenny nazywany również opisem Eulera jest odwrotnością opisu Lagrange'a. Współrzędne materialne są poszukiwaną funkcją współrzędnych przestrzennych. W opisie przestrzennym stawiamy pytanie która cząstka materialna $\X$ znajduje się w danej chwili czasu w danym (ustalonym) punkcie przestrzeni $\x$
$$\X = \X(\x,t).$$Opis ten używany jest głównie w mechanice płynów.
Opis materialny vs. opis przestrzenny
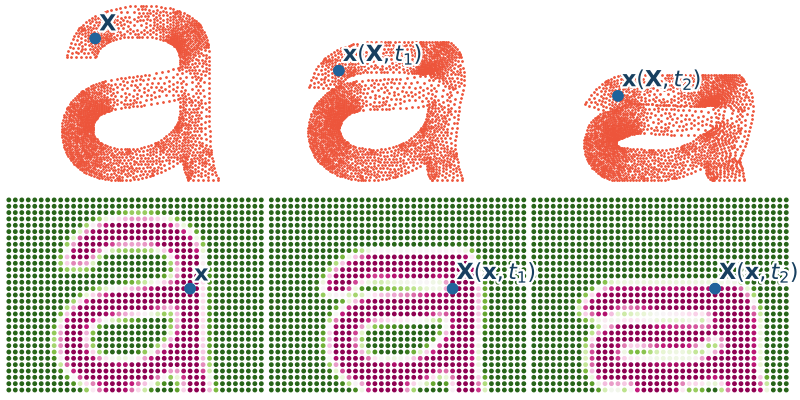
Wektor przemieszczenia
Wektor łączący początkową pozycję danego punktu materialnego z jego aktualną pozycją po deformacji.
Pomijając argumenty funkcji tensorowej mamy
$$\u = \x-\X, \qquad u_i = x_i - X_i$$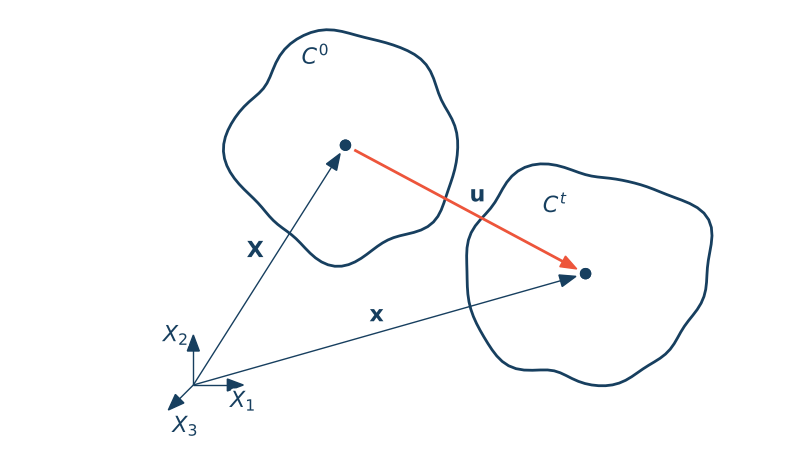
Gradient deformacji
W mechanice ośrodków ciągłych, gradient deformacji, często oznaczany jako $\F$, to tensor drugiego rzędu używany do opisu lokalnej deformacji materiału. Określa on związek pomiędzy deformacją cząstek materiału w początkowej (niezdeformowanej) konfiguracji a ich pozycjami w końcowej (zdeformowanej) konfiguracji.
• Materialny gradient deformacji
Matematycznie materialny gradient deformacji to pochodna cząstkowa aktualnej pozycji cząstki materialnej $\x$ po jej pozycji w konfiguracji odniesienie $\X$.
Gradient deformacji możemy przestawiać w reprezentacji macierzowej jako
gdzie $\nabla_{X}$ - gradient po współrzędnych materialnych ($\mathrm{Grad}$).
Gradient deformacji transformuje wektor $d\X$ na wektor $d\x = \F d\X$ - czyli opisuje deformację włókna materialnego $d\X$ (infinitezymalny element liniowy).
$$x_1 = \varphi_1(X_1, X_2, X_3,t),\quad x_1 = \varphi_1(X_j,t)$$ $$x_2 = \varphi_2(X_1, X_2, X_3,t),\quad x_2 = \varphi_2(X_j,t)$$ $$x_3 = \varphi_1(X_1, X_2, X_3,t),\quad x_3 = \varphi_3(X_j,t)$$ $$x_i = \varphi_i(X_j,t),\quad d \x = \mathbf{\varphi}(\X,t)dx_i = \pp{x_i}{X_j}dX_j = F_{ij} dX_j, \quad d\x = \pp{\x}{\X}d\X = \F d\X$$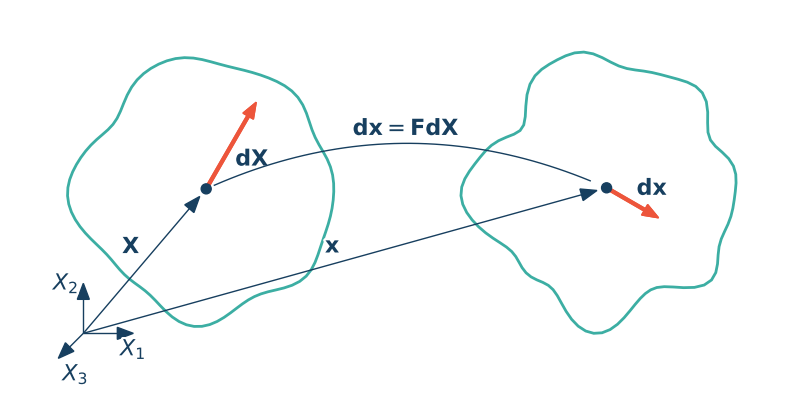
Przykłady gradientu deformacji dla rożnego rodzaju ruchów
• dla ruchu sztywnego:
$$\F = \R(t)$$
• dla wydłużenia:
$$[F_{ij}]=\left[\begin{array}{ccc}1+\alpha(t)&0&0\\0&1&0\\0&0&1\end{array}\right]$$
• dla ścinania:
$$[F_{ij}]=\left[\begin{array}{ccc}1&\gamma(t)&0\\0&1&0\\0&0&1\end{array}\right]$$
Jeżeli równanie ruchu w opisie Lagrange'a zapiszemy jako $\x=\F\X$ gdzie $\F$ jest stałym tensorem to otrzymujemy równanie opisujące jednorodną deformację. Różniczkując równanie ruchu otrzymujemy, że tensor $\F$ jest gradientem deformacji. Na poniższym rysunku przedstawiono geometryczne interpretacje deformacji jednostkowego kwadratu w zależności od postaci tensora $\F$.
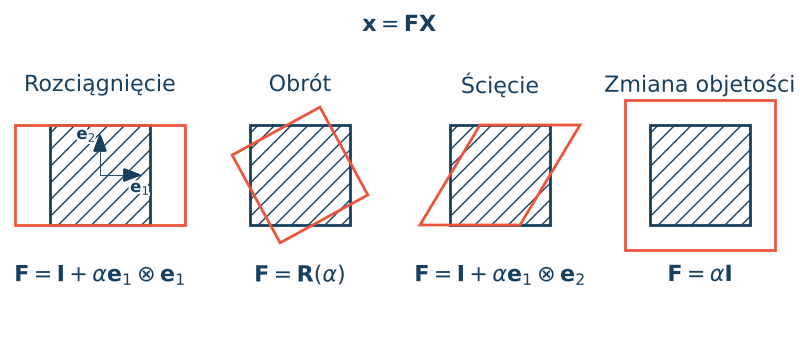
Własności gradientu deformacji $\F$
• wyznacznik musi być większy od zera
$$\det(\F)>0$$
• zgodnie z rozkładem polarnym gradient deformacji możemy rozłożyć na dwa tensory;
$$\F = \R\U = \V\R, \quad \U^2 = \F^T\F = \C, \quad \V^2 = \F\F^T$$
• tensor obrotu; dla ruchu sztywnego
$$\F=\R \rightarrow \U=\V=\I$$
Przestrzenny gradient deformacji
Materialny gradient deformacji jest odwrotnością przestrzennego gradientu i vice versa $\F = \f^{-1}$. W podobny sposób tensor $\f$ transformuje wektor $d\x$ na wektor $d\X: \, d\X = \f d\x$.
Gradient przemieszczenia
• materialny
• przestrzenny
• Związek gradientu deformacji z wektorem przemieszczenia
$$\x=\X+\u, \quad \F = \I+\cfrac{\partial\u}{\partial\X}$$ $$\F = \I + \H$$Tensor deformacji
Oznaczmy długość infinitezymalnego włókna materialnego przed deformacją jako $dL$ oraz po deformacji jako $dl$. Kwadrat długość zdeformowanego włókna materialnego będzie wynosił
$$(dl)^2 = d\x\cdot d\x = dx_i dx_i =(F_{ij}dX_j)(F_{ik}d X_k) =dX_j(F_{ij}\:F_{ik})dX_k =dX_j\:C_{jk}\: d X_k = d \X \C d \X,$$gdzie tensor drugiego rzędu $\C$ jest nazywany tensorem deformacji i jest on dodatnio określony.
Analogiczne rachunki możemy przeprowadzić dla kwadratu długości włókna w konfiguracji początkowej wykorzystując opis przestrzenny
$$(dL)^2 = d\X\cdot d\X = dX_i dX_i =(f_{ij}dx_j)(f_{ik}dx_k) =dx_j(f_{ij}\:f_{ik})dx_k =dx_j\:c_{jk}\: d x_k = d \x \c d \x$$ $$c_{jk} = f_{ij}f_{ik}, \, \c = \f^T\f$$Tensor odkształcenia Greena
Rozważmy różnice kwadratów długości włókna przed i po deformacji. Oznaczmy te długości odpowiednio jako $dL$ - długość początkowa włókna, $dl$ - długość włókna po deformacji.
$$(dl)^2 - (dL)^2 = dx_idx_i -dX_jdX_j = (C_{jk}-\delta_{jk}) dX_jdX_k =2\cfrac{1}{2}(C_{jk}-\delta_{jk}) dX_jdX_k = 2 E_{jk} dX_jdX_k$$Analogiczne rachunki możemy przeprowadzić w opisie przestrzennym. Dostajemy wtedy tensor odkształcenia Almansiego:
Miary odkształcenia
$$\E = \cfrac{1}{2m}\left(\U^{2m} -\I \right), \, E_{ij} = \cfrac{1}{2m}\left(U_{ij}^{2m} - \delta_{ij} \right)$$• Green dla $m=1: \qquad$ $\E = \cfrac{1}{2}\left(\U^{2}-\I\right)$
• Biot dla $m=1/2: \qquad$ $\E = \U-\I$
• Hencky dla $m=0: \qquad$ $\E = \ln\U$
• Almansi dla $m=-1: \qquad$ $\E = \cfrac{1}{2}\left(\I-\U^{-2}\right)$