Wprowadzenie

Do tej pory sprowadzaliśmy wszystkie analizowane zagadnienia do prostych przypadków jednowymiarowych. Wprowadzone zostały miary odkształcenia i naprężenia, które pozwalają określić w sposób liczbowy deformację i wytężenie materiału. Dla trójwymiarowych zagadnień wprowadzone miary nie mogą być dalej stosowane. Do określenia stanu deformacji i naprężenia musimy używać tensorów.

Zapis

Tensory rzędu pierwszego skalary będziemy zapisywać małymi literami, wektory małymi pogrubionymi literami lub z podkreśleniem na dole, tensory drugiego i wyższych rzędów dużymi literami z podkreśleniem lub pogrubioną czcionką.
• skalary (tensory zerowego rzędu) - $\quad a, b, \alpha, \beta$
• wektory (tensory pierwszego rzędu) -$\quad \underline{a},\a, a_i$
• tensory drugiego i wyższego rzędu $\quad \underline{A},\A, A_{ij}, B_{ijk}$

Konwencja sumacyjna

Konwencja sumacyjna Einsteina, znana także jako konwencja sumacyjna, to zapis matematyczny, który upraszcza notację w rachunku tensorowym. Zasada ta pozwala na zapisywanie wielu równań w bardziej zwięzły sposób poprzez eliminację znaków sumacyjnych.

Dla przykładu rozważmy zapis sumy składowych dwóch wektorów

$$s = a_1x_1 + a_2x_2+a_3x_3+...+a_n x_n$$ $$s = \sum_{i=1}^{n}a_ix_{i}$$

gdzie $i$ - indeks niemy, można zmienić jego nazwę bez żadnych konsekwencji.

$$s = a_ix_{i}$$

Jeśli w wyrażeniu występuje indeks powtarzający się w jednym składniku, oznacza to, że dokonuje się sumowania po tym indeksie. Sumowanie odbywa się po wszystkich możliwych wartościach tego indeksu, od dolnego do górnego zakresu. Konwencja jest czasem nazywana notacją Einsteina.

Notacja

trzy rodzaje: wskaźnikowa, absolutna, macierzowa. Spróbujmy zapisać operacje iloczynu skalarnego dwóch takich samych wektorów w odpowiednio trzech zapisach: wskaźnikowym, macierzowym i absolutnym.

$$a = v_iv_i, \quad a = \v \v^T,a = \v\v$$

W zapisie absolutnym nie musimy przejmować się transpozycją. Uwaga na zapis wektora jako "wektora wierszowego" lub "wektora kolumnowego". W różnych programach i bibliotekach matematycznych stosuje się różne konwencje.

$$\v = \vc{v_1}{v_2}{v_3} \quad \lor \quad \v = \vr{v_1}{v_2}{v_3}$$

Delta Kroneckera

To symbol matematyczny powszechnie używane w algebrze liniowej i fizyce. Wprowadzony został przez niemieckiego matematyka Leopolda Kroneckera aby uprościć wyrażenia oparte na tensorach.

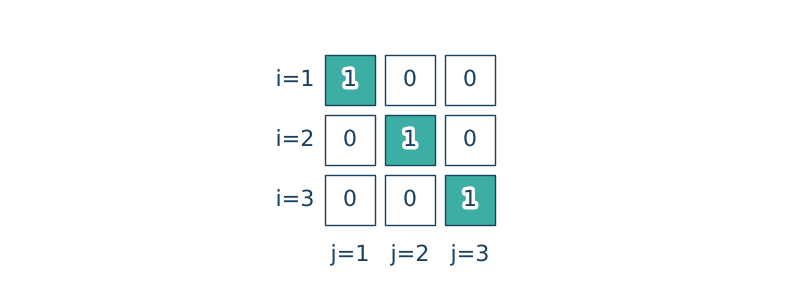
Delta Kroneckera $\delta_{ij}$ jest zdefiniowana następująco

$$\delta_{ij}=1 \txt{if} i=j$$ $$\delta_{ij}=0 \txt{if} i \neq j$$

Właściwości:

$$\delta_{ij} = \delta_{ji}, \quad \delta_{ii} = 3, \quad \delta_{im}a_{m} = a_i, \quad \delta_{im}T_{mj} = T_{ij}$$

O poszczególnych składowych $\delta_{ij}$ można myśleć jako macierzy jednostkowej o wymiarze $3\times 3$ (macierz diagonalna o wszystkich wartościach na przekątnej głównej równych 1).

Symbol permutacyjny

Znany jest również jako symbol Levi-Civita lub tensor całkowicie antysymetryczny. $\epsilon_{ijk}$ jest symbolem matematycznym ułatwiającym i upraszczającym zapisywanie operacji na tensorach.

$$\epsilon_{ijk} = 1 \txt{if} i, j, k = 123 \lor 231 \lor 321$$ $$\epsilon_{ijk} = -1 \txt{if} i, j, k = 132 \lor 213 \lor 312$$ $$\epsilon_{ijk} = 0 \txt{otherwise}$$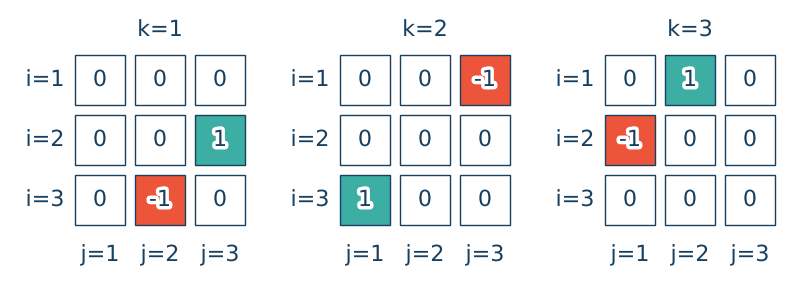

Właściwości

$$\epsilon_{ijk} = \epsilon_{jki} = \epsilon_{kij}, \quad\epsilon_{ijk} = -\epsilon_{jik}$$

Przestrzeń fizyczna

Wszystko będziemy definiować w kartezjańskim układzie współrzędnych o początku w punkcie 0, Punkty będą określane jednoznacznie przez trójki liczb $(x_1,x_2,x_3)$. W tego typu układach zanika różnica miedzy współrzędnymi kowariantnymi i kontrawariantnymi oraz między bazą i kobazą.

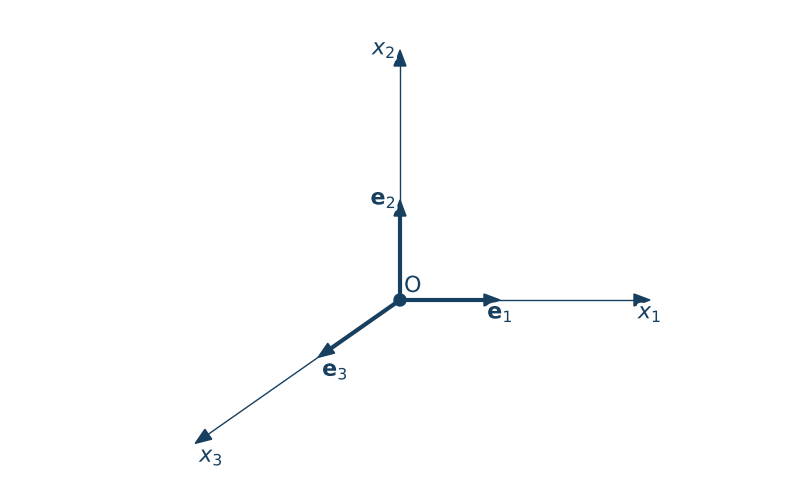
wersory osi układu współrzędnych $\e_i$:$[1\,0\,0]$, $[0\,1\,0]$, $[0\,0\,1]$; $\e_i\cdot\e_j = \delta_{ij}$, dla układów prawoskrętnych: $\e_i\times\e_j = \epsilon_{ijk}\e_k$,

Rozkład wektora w bazie

$$\v_{i} = v_1\e_1+ v_2\e_2 + v_3\e_3 = \sum_{i=1}^{3} v_i\e_{i} = v_i\e_i$$

Zmiana bazy w przestrzeni - przekształcenie ortogonalne

Rozważy dwie bazy: starą zdefiniowaną przez wektory $\e_i$ oraz nową oznaczoną wektorami $\e'_i$. Spróbujmy wyrazić wektory nowej bazy przez kombinacje liniowe wektorów bazy starej. Rozpatrzmy przekształcenie ortogonalne wyrażone tensorem $\Q$. Przy translacji układu współrzędnych wektory bazowe nie ulegają zmianie więc nie będziemy się takim przekształceniem zajmować.

$$\e'_i = \Q \e_i$$

gdzie $\Q$ jest macierzą przekształcenie ortogonalnego. Wartości macierzy $\Q$ będą stanowiły odpowiednie wartości kosinusów kierunkowych czyli liczby opisujące wartości rzutów wektorów nowej bazy na wektory bazy starej.

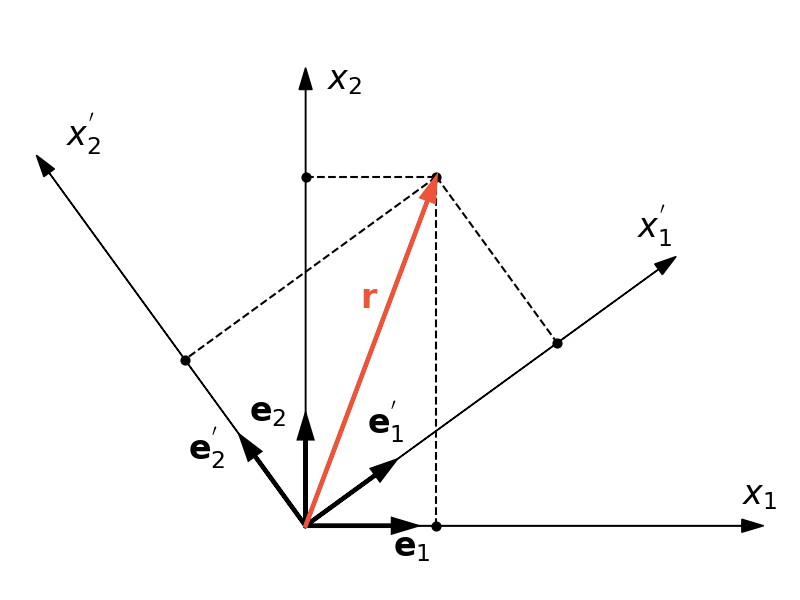
Rozpisując tensor $\Q$ jako macierz współczynników w stowarzyszeniu bazowym $\e_m\otimes\e_n$ dostajemy

$$\e'_i = (Q_{mn}\e_m\otimes\e_n)\e_i = Q_{mn}\e_m\otimes\e_n \cdot \e_i = Q_{mi}\e_m \delta_{ni}=Q_{mi}\e_m$$

Zmieniając nazwy indeksów dostajemy

$$\e'_i = Q_{ji}\e_j$$

Jeżeli przemnożymy powyższe równanie obustronnie prze $\e_m$ dostaniemy

$$\e'_i \e_m = Q_{ji}\e_j \e_m = Q_{ji}\delta_{jm} = Q_{mi}$$

Wyraźmy dowolny wektor $\v$ w dwóch bazach

$$\v = v_i\e_i = v'_i \e'_i$$

Przemnażając obydwie strony przez $\e_j$ dostajemy

$$v_i\e_i \cdot \e_j = v'_i \e'_i \cdot \e_j \rightarrow v_i \delta_{ij} = v'_i Q_{ji} \rightarrow v_j = v'_i Q_{ji}$$

Podsumowując prawo transformacji współrzędny wektora z nowe bazy do starej wygląda następująco

$$v_i = Q_{ij} v'_j$$

Odwrotne prawo transformacji otrzymamy przemnażając otrzymane prawo transformacji przez $Q_{ik}$

$$v_i Q_{ik} = Q_{ik}R_{ij} v'_j \rightarrow v_i Q_{ik} = \delta_{ik} v'_i \rightarrow v_i Q_{ik} = v'_k$$

Zmieniając indeksy ($k\rightarrow i, i \rightarrow j$) mamy

$$v'_i = Q_{ji} v_j$$

---

Prawo transformacji dla współrzędnych wektora mozemy również uzyskać wykonując następujące operacje. Rozważmy tak jak wcześniej dowolny wektor $\v$ który ma składowe $v_i$ w starym układzie i $v'_i$ w nowym układzie. Zapiszmy wektor $\v$ w obu tych bazach wykorzystując prawo transformacji dla wektorów bazowych czyli $e_j = Q_{ji} \e'_i$

$$\v = v'_i\e'_i = v_j\e_j = v_j (Q_{ji}\e'_i) = (v_j Q_{ji}) \e'_i$$

Porównując odpowiednie współczynniki przy wektorach bazowych w nowej bazie $\e'_i$ mamy

$$v'_i = Q_{ji} v_j$$

Analogicznie możemy wyprowadzić związek odwrotny czyli

$$\v = v_i\e_i = v'_j\e'_j = v'_j (Q_{ij}\e_i) = (v'_j Q_{ij})\e_i$$ $$v_i = Q_{ij} v'_j$$

Podsumowując otrzymaliśmy następujące prawa transformacji

• dla wektorów bazowych

$$\e'_i = Q_{ji} \e_j, \quad \e_i = Q_{ij} \e'_j$$

• dla współrzędnych wektora

$$v'_i = Q_{ji} v_j, \quad v_i = Q_{ij} v'_j$$

Uwaga! W literaturze często używa się odwrotnego zapisu, mianowicie kolejne wektory nowej bazy wstawiane są w kolejne wierszy macierzy $\Q$ wtedy prawa transformacji są następujące

$$\e'_i = Q_{ij} \e_j, \quad \e_i = Q_{ji} \e'_j$$

• dla współrzędnych wektora

$$v'_i = Q_{ij} v_j, \quad v_i = Q_{ji} v'_j$$

Skalar (tensor rzędu zerowego)

wielkość fizyczna, opisywana przez liczbę rzeczywistą, której wartość nie zależy od zmian układu odniesienia. Prawo transformacji:

$$m' = m$$

• przykłady nie-skalarów: poszczególne współrzędne punktów
• przykłady skalarów: masa, temperatura, odległość punktów, ciśnienie

Wektor (tensor rzędu pierwszego)

wielkość fizyczna $\v$, opisywana w danym układzie współrzędnych przez trójkę liczb rzeczywistych $[\,v_1\;v_2\;v_3\,]$ o wartościach (i) niezmieniających się w wyniku translacji układu współrzędnych oraz (ii) transformujących się wg wzoru

przy jego obrocie i/lub odbiciu symetrycznym.

• przykłady nie-wektorów: współrzędne punktów
• przykłady wektorów: przemieszczenie, prędkość, siła

Sumowanie wektorów i mnożenie przez skalar daje również wektor -- spełnienie warunków przestrzeni liniowej

iloczyn skalarny - operacja zdefiniowana jako $\v\cdot\w = v_iw_i$. Wynik jest skalarem. Jeżeli

$$|\w|=1, \quad \text{to} \quad \v\cdot\w$$

jest długością rzutu $\v$ na kierunek $\w$

norma (długość) wektora (niezmiennik): $|\v| = \sqrt{\v\cdot\v}$

kąt między wektorami $\cos\alpha = \frac{\v\cdot\w}{|\v| |\w|}$

iloczyn wektorowy - operacja zdefiniowana jako $\u=\v\times\w, u_k=v_iw_j\epsilon_{ijk}$ dokładna postać składowych:

$$= [\:v_2w_3-v_3w_2\:,\:v_3w_1-v_1w_3\:,\:v_1w_2-v_2w_1\:]$$

Własności iloczynu wektorowego:

• $\v\times\w = -\w\times\v$ - przestawienie wskaźników w symbolu permutacyjnym sprawdza się do dodaniu minusa
• $\v\times\v = \o, \quad v_iv_j\epsilon_{ijk}=0$ - weźmiemy tyle same wyrazów z plusem co z minusem
• $(\v\times\w)\cdot\v=v_iw_jv_k\epsilon_{ijk} = 0$, to samo dla $(\v\times\w)\cdot\w$, $v_iv_k = \delta_{ik}$ a wiec $\delta_{ik}\epsilon_{ijk}=0$

Wynik iloczynu wektorowego jest prostopadły do czynników. Jego długość jest równa polu równoległoboku rozpiętego na wektorach-czynnikach.