Podstawowe pojęcia w opisie jednowymiarowym
przemieszczenie - wektor łączący położenie początkowe punktu materialnego z jego położeniem końcowym. Dla dowolnego ruchu krzywoliniowego wartość tego wektora jest mniejsza bądź równa drodze pokonanej przez ciało. Jeżeli różne punkty mają rożne wektory przesunięcia to mamy do czynienie z deformacją (oprócz ruchu obrotowego).
$$u(X,t) = x(X,t) - X,\qquad \text{[m]}$$
prędkość - zmiana położenia punktu materialnego w czasie. Możemy też zapisać prędkość wykorzystując przemieszczenie bo pochodna względem czasu z $X$ jest równa zero.
$$v(X,t) = \cfrac{\partial x(X,t)}{\partial t} = \cfrac{ \partial u(X,t)}{\partial t}\qquad \text{[m/s]}$$
przyśpieszenie - wielkość fizyczna zdefiniowana jako pochodna prędkości po czasie, czyli przyśpieszenie jest szybkością zmiany prędkości.
$$a(X,t) = \cfrac{\partial v(X,t)}{\partial t}, \qquad \text{[m/s${^2}$]}$$
odkształcenie -miara deformacji ciała poddanego działaniu obciążeń termiczno-mechanicznych. Dla przypadku jednowymiarowego możemy zdefiniować odkształcenie jako:
$$\varepsilon(X,t) = \cfrac{\partial u(X,t)}{\partial X},\qquad \text{[-]}$$
prędkość odkształcenia - gradient prędkości punktu materialnego.
$$\dot{\varepsilon}(X,t) = \cfrac{\partial v(x,t)}{\partial x},\qquad \text{[1/s]}$$
siła - wektorowa wielkość fizyczna będąca miarą oddziaływań fizycznych między ciałami. Pojęcie siły skupionej występujące w fizyce i technice jest pewną idealizacją obciążeń rzeczywistych. Siła skupiona, w ścisłym znaczeniu tego słowa, w realnej rzeczywistości nie istnieje. Jednostką siły jest newton $N$.
naprężenie - gęstość sił wewnętrznych w danym punkcie ciała
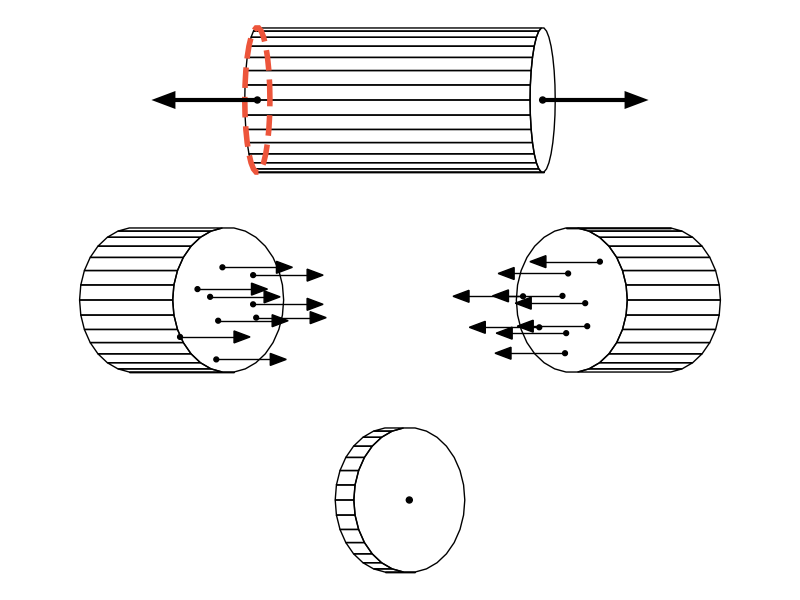
gdzie $\sigma$ - naprężenie, $P$ - siła, $A$ - pole przekroju pręta (w płaszczyźnie prostopadłej do działającej siły)
temperatura - jedna z podstawowych wielkości fizycznych (parametrów stanu) w termodynamice. Temperatura jest związana ze średnią energią kinetyczną ruchu i drgań wszystkich cząsteczek tworzących dany układ i jest miarą tej energii. Temperatura jest miarą średniej energii kinetycznej atomów lub cząsteczek w układzie.
$$T(x, t) \qquad \text{[K]}$$
gradient temperatury -temperatura prezentujemy zazwyczaj na konfiguracji aktualnej. Jej gradient jest liczony na tej konfiguracji.
$$\cfrac{\partial T(x, t)}{\partial x} \qquad \text{[K/m]}$$
ciepło - ilość energii wewnętrznej przekazywanej w procesie cieplnym
$$Q(x, t) \qquad \text{[J]}$$
strumień ciepła – prędkość przepływu ciepła. Może być wyrażony przez stosunek elementarnej ilości ciepła $dQ$ do czasu trwania wymiany tej ilości ciepła $dt$ (czasu trwania przepływu elementarnej ilości ciepła), czyli jest to pochodna po czasie ilości ciepła przepływającego przez przekrój poprzeczny przegrody.
$$\dot{Q}(x, t) = \cfrac{\partial Q}{\partial t} \qquad \text{[W=J/s]}$$
gęstość strumienia ciepła stosunek elementarnego strumienia ciepła $d\dot{Q}$ do elementarnego pola powierzchni $dA$ w płaszczyźnie prostopadłej do kierunku przepływu ciepła
$$q(x,t) = \cfrac{d\dot{Q}(x,t)}{dA}, \qquad \text{[W/m$^2$]}$$
Podstawowe własności mechaniczne materiałów
gęstość -stosunek masy pewnej ilości substancji do zajmowanej przez nią objętości
$$\rho(x,t), \qquad \text{[kg/m$^3$]}$$
| Materiał | Guma | Beton | Stal | Drewno | Kość |
|---|---|---|---|---|---|
| $\rho$ [kg/m$^3$] | 1300 | 2500 | 7800 | 800 | 600 |
sztywność - wielkość określająca zdolność ciała do przeciwstawiania/poddawania się odkształceniu wywołanemu przez obciążenie, odwrotność to podatność.
| Materiał | Guma | Beton | Stal | Drewno | Kość |
|---|---|---|---|---|---|
| E [GPa] | 0.01 | 30 | 210 | 11 | 15 |
współczynnik przewodzenie ciepła informuje o strumieniu energii, jaki przepływa przez jednostkową powierzchnię warstwy materiału o grubości $1m$, przy różnicy temperatury po obydwu stronach tej warstwy $1K (1^{\circ}C)$.
| Materiał | Guma | Beton | Stal | Drewno | Kość |
|---|---|---|---|---|---|
| $\lambda$ [W/(m $\cdot$ K)] | 0.3 | 2 | 58 | 0.2 | 0.6 |
ciepło właściwe - ciepło potrzebne do zmiany temperatury ciała o jednostkowej masie o jedną jednostkę. Jest współczynnikiem pozwalającym określić skłonność ciała do łatwiejszej lub trudniejszej zmiany temperatury pod wpływem dostarczonej energii cieplnej.
| Materiał | Guma | Beton | Stal | Drewno | Kość |
|---|---|---|---|---|---|
| c [J/(kg $\cdot$ K)] | 2000 | 1000 | 500 | 2400 | 1200 |
rozszerzalność termiczna - zdolność ciała do zmiany kształtu pod wpływem zmiany temperatury. Współczynnik określający o ile zmieni się długość ciała po podniesieniu temperatury o jeden stopień określamy jako $\alpha$. Występuje też ujemna rozszerzalność termiczna tzn. po podgrzaniu ciało kurczy się. Zmianę długości pręta pod wpływem przyrostu temperatury możemy wyrazić jako
$$l = L (1 + \alpha \Delta T),$$
gdzie $L$ to długość pręta przed deformacją a $l$ to długość pręta po deformacji.
| Materiał | Guma | Beton | Stal | Drewno | Kość |
|---|---|---|---|---|---|
| $\alpha$ [1/K] | $80 \cdot 10^{-6}$ | $12 \cdot 10^{-6}$ | $11 \cdot 10^{-6}$ | $5 \cdot 10^{-6}$ | - |
wytrzymałość - określa naprężenie potrzebne do zniszczenia materiału pod wpływem zadanego obciążenia. np. wytrzymałość na rozciąganie, ściskanie, zginanie.
| Materiał | Guma | Beton | Stal | Drewno | Kość |
|---|---|---|---|---|---|
| $R$ [MPa] | 16 | 30 | 200 | 40 | 60 |
jednorodność - jednakowe własności ciała we wszystkich punktach materialnych. Własności materiału nie zależą od położenia punktu materialnego.
izotropia/anizotropia - izotropia oznacza jednakowe własności mechaniczne materiału niezależne od kierunku badania. Przeciwieństwem izotropii jest anizotropia.
Prawa i związki fizyczne
Zachowaniem mechanicznym konstrukcji rządzą powszechnie znane prawa (równania równowagi, ciągłości, przewodnictwa cieplnego, itp.), które w ujęciu kontynualnym przybierają postać nieliniowego układu równań różniczkowych na pola skalarne, wektorowe i tensorowe.
zasada zachowania masy - masa ciała w czasie nie ulega zmianie (istnieją układy o zmiennej masie np. rakieta która w czasie lotu spala swoje paliwo) takimi układami nie będziemy się zajmować.
$$m = \text{const}$$
zasada zachowania pędu - zmiana pędu równa jest wypadkowej sile
$$\cfrac{dP}{dt} = F$$
zasada zachowania momentu pędu (krętu) - zmiana momentu pędu jest równa wypadkowemu momentowi działającemu na ciało. Jednostką momentu jest [N$\cdot$m]
$$\cfrac{dK}{dt} = M$$
zasada zachowania energii mechanicznej Energia kinetyczna + potencjalna = const. W energii kinetycznej uwzględniamy jeszcze energię wewnętrzną związaną z deformacją.
prawo Hooke'a - związek konstytutywny (zostanie on szerzej omówimy w dalszej części wykładu) zależność między naprężeniem a odkształceniem. Dla przypadku jednowymiarowego prawo to można zapisać jako
$$\sigma = E \varepsilon,$$
gdzie $\sigma$ - naprężenie, $E$ - moduł Younga oraz $\varepsilon$ - odkształcenie
prawo Fouriera - prawo, dotyczące przewodnictwa cieplnego, stwierdzające, że gęstość strumienia ciepła jest proporcjonalna do gradientu temperatury.
$$q(x) = -\lambda \cfrac{dT(x)}{dx}$$gdzie $\lambda$ - współczynnik przewodzenia ciepła, $T(x)$ - temperatura, $q(x)$ - strumień ciepła.
Zagadnienie rozciągania pręta
Rozpatrzmy najprostszy przypadek ciała które może się deformować. Będzie to zagadnienie rozciągania pręta jednowymiarowego. Takie "hello world" z mechaniki ciał odkształcalnych. Zacznijmy od rzeczywistości.
Model fizyczny
Rozważmy pręt (ciało którego jeden wymiar jest zdecydowanie większy niż dwa pozostałe i jego oś jest prostą). Pręt ten ma pewien przekrój poprzeczny $A$ oraz długość $L$. Na pręt działa siła $P$ przyłożona na jego końcu oraz obciążenie wynikając z ciężaru własnego $q$. Grawitacja $g$ działa zgodnie z przyjętym układem współrzędnych. Rozważamy tylko oś pręta. To co dzieje się dla punktów materialnych leżących poza osią jest utożsamiane z rozwiązaniem dla osi. Zastosowaliśmy wiele uproszczeń, miejmy tego świadomość. Przeprowadźmy krótką analizę jednostki w jakiej wyrażone jest obciążenie ciągłe $q$.
$$q = g\cdot \rho \cdot A, \qquad \left[\cfrac{m}{s^2}\cfrac{kg}{m^3} \cdot m^2\right], \left[\cfrac{kg}{s^2}\right], \quad N = \cfrac{kg \cdot m}{s^2}, \qquad \left[\cfrac{N}{m}\right]$$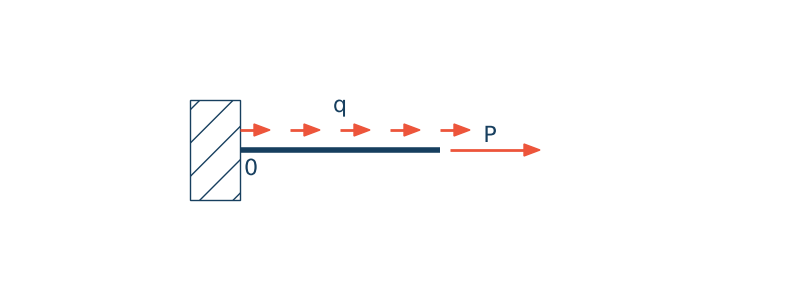
Model matematyczny
Załóżmy, że deformacje są małe ($X \approx x$) oraz że nasze zmienne nie zależą od czasu, tzn interesuje nas to co wydarzy się bardzo długim czasie kiedy wszystko się ustali. Nie musimy wtedy używać pochodnych cząstkowych. W przypadku jednowymiarowym zanika różnica w zapisie wektorów i skalarów pamiętajmy jednak o tym co w naszym równaniu jest wektorem a co skalarem.
Korzystając z warunku równowagi statycznej możemy zapisać (ciało pozostaje w spoczynku dlatego nie uwzględniamy sił bezwładności.)
$$-N(x) + N(x) + dN(x) + q(x)dx = 0.$$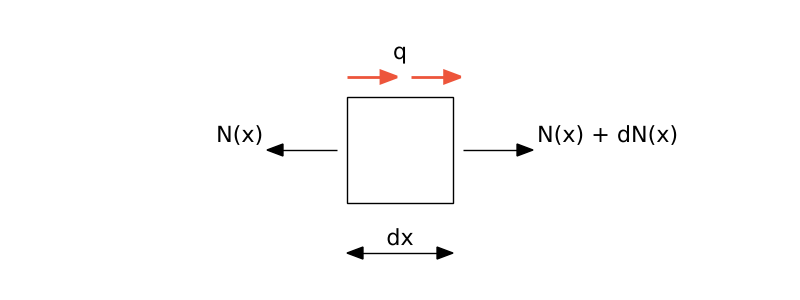
Po przekształceniach dostajemy
$$\cfrac{dN(x)}{dx} + q = 0.$$Siłę stanowi suma naprężeń na całym przekroju. Jeśli naprężenia są stałe w przekroju pręta, to możemy je określić z zależności
$$\sigma(x) = \cfrac{N(x)}{A}.$$Z powyższej zależności wyliczamy siłę jako
$$N(x) = \sigma(x)A.$$Równanie geometryczne (Cauchy’ego) wiążące ze sobą przemieszczenia i odkształcenia jest dane wzorem
$$\varepsilon(x) = \cfrac{du(x)}{dx}.$$
Wykorzystując równanie konstytutywne, Hooke'a określające zależność odkształcenia od naprężenia mamy
$$\sigma(x) = E\varepsilon(x),$$gdzie $E$ - moduł Younga, moduł odkształcalności sprężystej, zależny od materiału.
W dalszej kolejności możemy zapisać że
$$N(x) = EA(x)\cfrac{du(x)}{dx}.$$Ostatecznie dostajemy równanie
$$\cfrac{d}{dx}\left( EA\cfrac{du(x)}{dx} \right) + q = 0,\qquad 0 \leq x \leq L.$$które po prostych przekształceniach można zapisać jako
$$EA\cfrac{d^2u(x)}{dx^2} + q = 0.$$Rozwiązaniem powyższego równania różniczkowego jest nieskończenie wiele funkcji. Aby wybrać z pośród nich jedno rozwiązanie musimy sformułować warunki brzegowe dla rozważanego pręta. Równanie jest drugiego rzędu, zatem wymagane są dwa warunki brzegowe, ustalające wartość przemieszczenia $u$ lub siły $P$. Z naszego zadania wiemy, że
$$u(x=0) = 0, \qquad N(x=L) = EA\left. \cfrac{du}{dx}\right|_{x=L} = P$$Postulujemy, że rozwiązanie jest w postaci
$$u(x) = ax^2+ bx + c, \qquad \cfrac{du}{dx} = 2ax+ b, \qquad \cfrac{d^2u}{dx^2} = 2a.$$Wstawiając drugą pochodną do równania różniczkowego otrzymujemy
$$EA \cdot 2a + q = 0 \rightarrow a = -\cfrac{q}{2EA},$$a więc nasze rozwiązanie jest postaci:
$$u(x) = -\cfrac{q}{2EA}x^2 + bx + c$$Współczynniki b i c znajdujemy wykorzystując warunki brzegowe
$$a \cdot 0^2 + b \cdot 0 + c = 0 \rightarrow c = 0,$$ $$EA (2a \cdot L + b) = P \quad \rightarrow \quad b = \cfrac{P}{EA} - 2aL = \cfrac{P}{EA} + \cfrac{qL}{EA}.$$Nasze rozwiązanie ma następująca postać
$$u(x) = \cfrac{1}{EA} \left[-\cfrac{1}{2}qx^2 + \left(P + qL\right)x\right].$$Różniczkują powyższe równanie dostajemy funkcję odkształcenia
$$\varepsilon = \cfrac{1}{EA} \left(-qx + P + qL \right)$$oraz przemnażając wynik przez $EA$ dostajemy funkcje siły w pręcie
$$\qquad N(x)= -qx + P + qL.$$Prostym sprawdzeniem poprawności uzyskanego rozwiązania jest obliczenie siły dla najbardziej wytężonego przekroju czyli dla $x=0$. Siła jest równa $P+qL$ (obciążenie końca pręta plus cały jego ciężar).
Inne warianty zadania:
1) zadane przemieszczenie na końcu pręta,
2) pręt ściskany,
3) dwie siły przyłożone do końców pręta,
4) różne materiały na długości pręta,
5) zmienne pole przekroju $A(x)$,
6) zmienna sztywność na długości pręta $E(x)$,
7) zmienne obciążenie na długości pręta $q(x)$.
Ustalony przepływ ciepła
Zagadnienie to stanowi pełną analogię do zagadnienia rozciągania pręta: temperatura $T$ $\Rightarrow u $, strumień ciepła $Q$ $\Rightarrow N$, gęstość strumienia ciepła $q$ $\Rightarrow \sigma$, wewnętrzne źródła ciepła $r \Rightarrow q$, $E \Rightarrow \lambda$. Korzystając z bilansu energii ułożonego dla fragmentu pręta, czyli to co wpływa minus to co wypływa plus to co generuje się w środku ciała dostajemy:
$$Q(x) - (Q(x) + dQ(x)) + r = 0,$$gdzie $r$ oznacza wewnętrzne źródła ciepła.
Po przekształceniach dostajemy
$$-\cfrac{dQ(x)}{dx} + r = 0.$$Wykorzystując definicję gęstości strumienia ciepła możemy zapisać
$$q(x) = \cfrac{Q(x)}{A}$$Z powyższej zależności wyliczmy strumień ciepła
$$Q(x) = q(x)A.$$Z prawa Fouriera mamy
$$q(x) = -\lambda \cfrac{dT(x)}{dx},$$czyli
$$Q(x) = -\lambda A \cfrac{dT(x)}{dx}.$$Podstawiając do bilansu energii dostajemy
$$\lambda A \cfrac{d^2T(x)}{dx^2} + r = 0.$$Z powyższego równania możemy usunąć $A$ gdy odpowiednio określimy wewnętrzne źródła ciepła (podamy je na jednostkę długości).