Wprowadzenie

Mechanika

Mechanika jest jedną z gałęzi fizyki, która zajmuje się badaniem ruchu i sił działających na ciała. Jest to nauka, która analizuje zachowanie się obiektów materialnych pod wpływem różnych sił oraz studiuje prawa, które nimi rządzą.

Termomechanika

Termomechanika to dziedzina nauki, która łączy w sobie elementy mechaniki oraz termodynamiki. Zajmuje się badaniem zachowania się materiałów pod wpływem zarówno sił zewnętrznych, jak i zmian temperatury.

Ciało fizyczne

Ciało fizyczne to zbiór cząstek o niezerowej masie traktowany jako całość. W fizyce, termin "ciało fizyczne" odnosi się do obiektu materialnego, który zajmuje pewną przestrzeń i ma masę. Ciało fizyczne może być w formie stałej, ciekłej lub gazowej. Jest to podstawowy termin używany w fizyce do opisu materii, która jest obserwowalna i podlega badaniom.

Ciała fizyczne mogą mieć różne właściwości, takie jak kształt, objętość, masę, temperaturę itp. Mogą być jednorodne lub złożone z różnych substancji. Przykłady ciał fizycznych to: ludzkie ciało, przedmioty codziennego użytku, planety, gwiazdy itd.

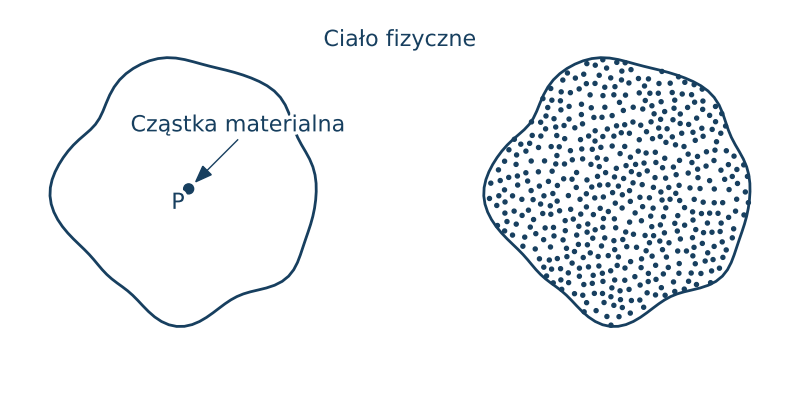
Ciało odkształcalne

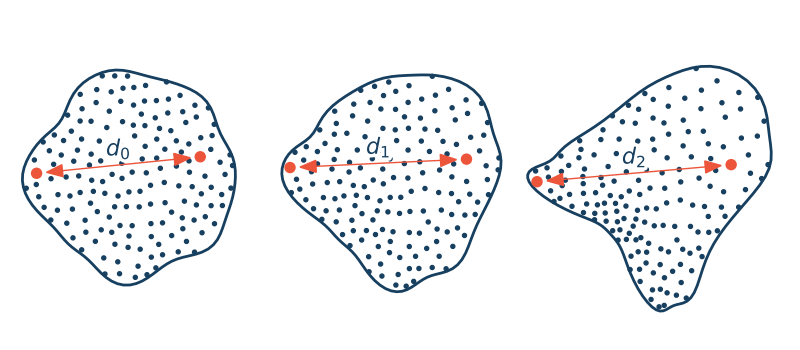
Ciało odkształcalne to ciało fizyczne, w którym wzajemne odległości cząstek mogą ulegać zmianie pod wpływem działających na nie sił. W rzeczywistości wszystkie ciała fizyczne są odkształcalne!

Podsumowanie

Tak więc Termomechanika Ciał Odkształcalnych to dziedzina nauki która zajmuje się badaniem ruchu ciał odkształcalnych pod wypływem przyłożonych obciążeń mechanicznych i termicznych.

Odkształcalność

Rozważmy prostą funkcję $y(x) = 2x$. Popatrzmy na tą funkcję jako przyporządkowanie punktom z jednej przestrzeni jednowymiarowej $x$ ich nowego położenia w drugiej przestrzeni $y$. Wyznaczmy położenia dla kilku wybranych punktów. Współrzędne na osi $x$ określają początkowe położenie punktów, natomiast współrzędne na osi $y$ ich położenia aktualne (po transformacji). Tą samą funkcję można przestawić jako deformację pręta z znaczoną "teksturą" która ułatwia wizualizacje lokalnej deformacji. Dziedzinę funkcji utożsamiać będziemy z początkowym położeniem pręta , a przeciwdziedzinę funkcji z konfiguracją zdeformowaną pręta.

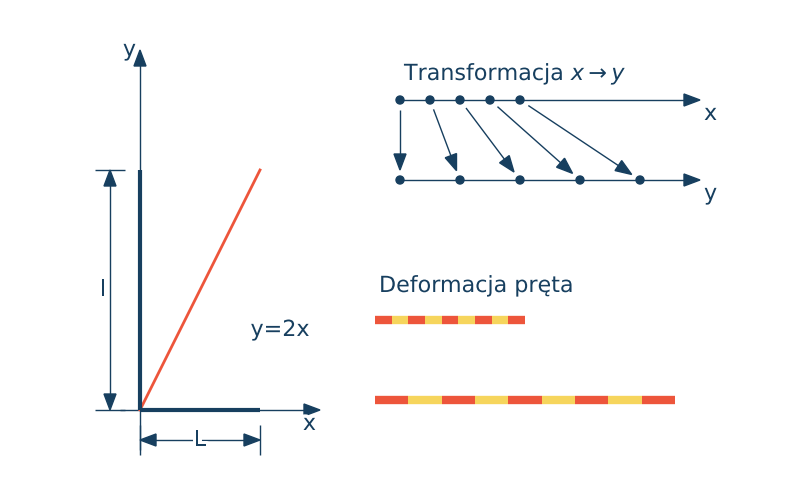
Analizując powyższy przypadek widzimy że pręt uległ wydłużeniu. Jego początkowa długość została podwojona. Parametr stojący przy zmiennej $x$ będzie odpowiadał za wydłużenie pręta. Przeanalizujmy różne inne postaci funkcji w odniesieniu do opisu deformacji pręta.

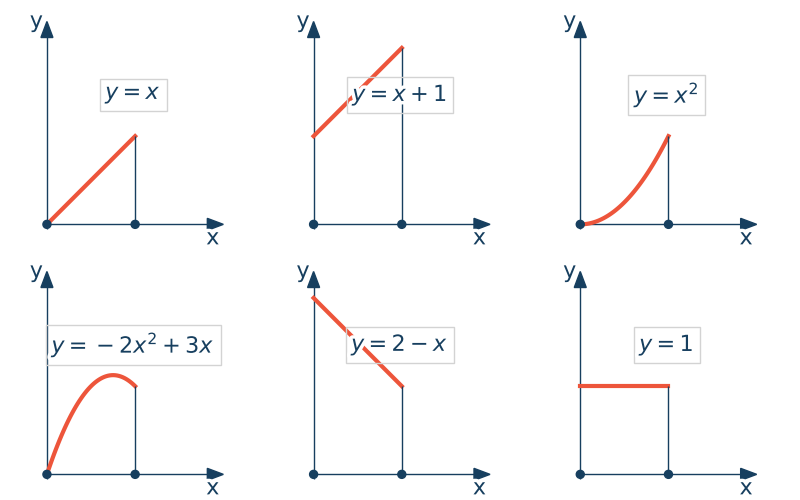
W przypadku funkcji $y(x)=x$ pręt nie ulega odkształceniu. Dodatnie $1$ do funkcji powoduje jednakowy przesuw całego pręta. Odległości miedzy punktami nie uległy zmianie, a wiec brak jest odkształcenia.

Rozważmy funkcję $y(x) = x^2$. Całkowita długość pręta nie zmienia się, natomiast odkształcenie na długości pręta ulega zmianie. Gdybyśmy patrzyli globalnie na nasz pręt moglibyśmy mylnie uznać, że pręt się nie odkształcił.

Nie każda funkcja może opisywać ruch ciała. Funkcja musi być różnowartościowa i posiadać funkcję odwrotną. Oznacza to fizyczne, że nie możemy "przenicować" ciała na drugą stronę. Widać wyrazie, że analizowana funkcja $y(x) = -2x^2+3x$ w przedziale $x\in(0,1)$ nie jest różnowartościowa. Podobnie wygląda sytuacja gdy pochodna funkcji jest mniejsza od zera.

Gdy pochodna jest równa $0$ dostajemy osobliwość. Długość pręta po deformacji wynosi 0.

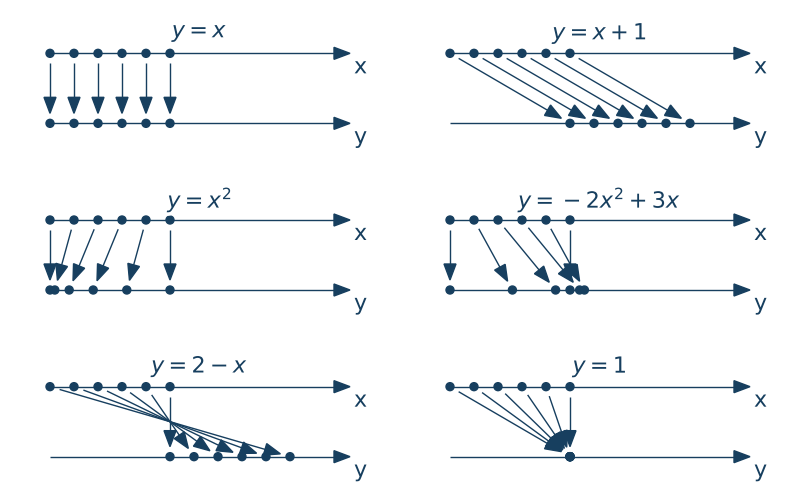
Interpretacja powyższych przypadków prowadzi do następujących wniosków:
• miarą odkształcenia jest pochodna w danym punkcie.
• Gdy wartość pochodnej jest większa od 1 otrzymujemy lokalne wydłużenie pręta, gdy mniejsza od 1 - skrócenie.
• wartość pochodnej w każdym punkcie musi być większa od zera
• funkcja opisująca deformację musi być funkcją różnowartościową.

Miara odkształcenia

Z powyższych przykładów możemy sformułować następującą definicję odkształcenia:

$$\varepsilon(x) = \cfrac{dy}{dx} - 1$$

Do wzoru dodajmy $-1$ bo chcemy aby w przypadku braku deformacji odkształcenie było równe $0$. Zapiszmy w dalszej kolejności funkcję $y(x)$ w trochę innej postać wykorzystując przemieszczenie punktu:

$$y(x) = x + u(x)$$

gdzie $u(x)$ będzie oznaczało przemieszczenie punktu $x$. Funkcję przemieszczenie możemy wyznaczyć w bardzo prosty sposób jako różnicę między aktualnym a początkowym położeniem punktu.

$$u(x) = y(x) - x$$

Wykorzystując definicje przemieszczenia wzór na odkształcenie wygląda następują:

$$\varepsilon(x) = \cfrac{dy(x)}{dx} - 1 = \cfrac{dx}{dx} + \cfrac{du(x)}{dx} - 1 = \cfrac{du(x)}{dx}$$

Podsumowując, odkształcenie w danym punkcie $x$ to pochodna przemieszczenia tego punktu. Ujemna wartość odkształcenia oznacza lokalne skrócenie, dodatnia wartość rozciągnięcie. Biorąc pod uwagę ograniczenia narzucone na funkcję $y(x)$ wartości odkształcenia spełniają następująca nierówność

$$-1 < \varepsilon(x) < \infty.$$

Wartość $-1$ oznacza że nasz pręt został ściśnięty do pojedynczego punktu. Z kolei dla rozciągania pręta nie ma ograniczenia na wartość odkształcenia. Widoczna jest tu asymetryczność między ściskaniem i rozciąganiem.