Analiza termiczno-mechanicza hamulca tarczowego
Zadanie polega na przeprowadzeniu analizy termiczno-mechanicznej fragmentu hamulca tarczowego.
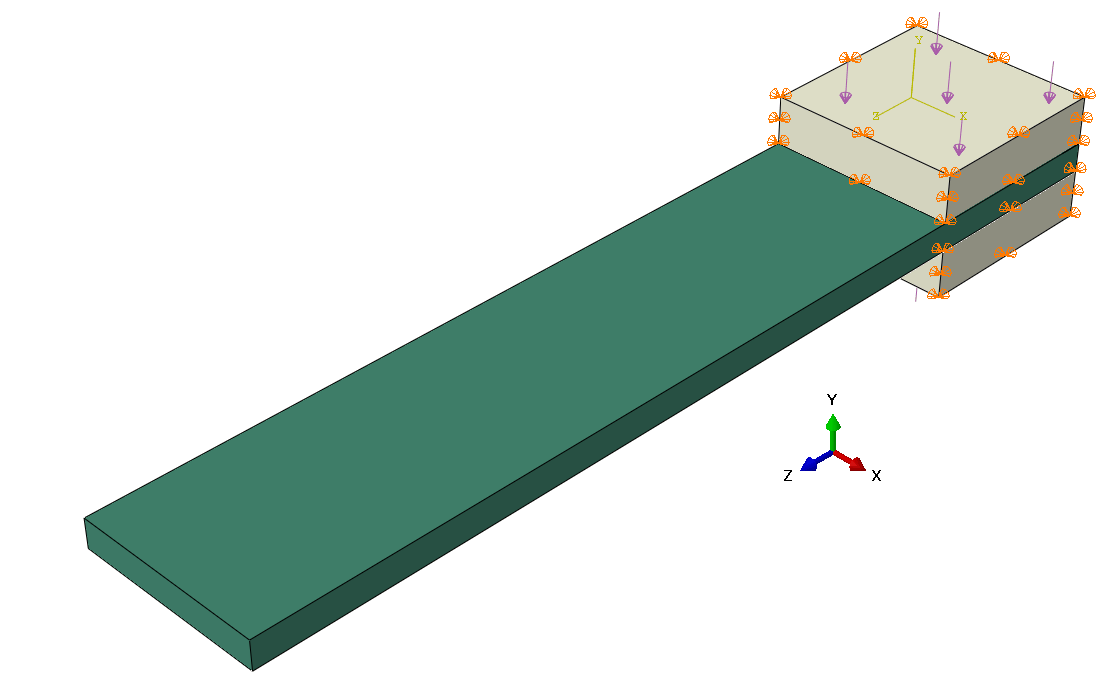
Geometria
Wszystkie ciała modelowanie są jako trójwymiarowe odkształcalne bryły. Model składa się z trzech części tak jak to przedstawiono na rysunku.
• fragment tarczy (prostopadłościan) ,
• 2 x klocek hamulcowy (prostopadłościan),
Obydwa klocki mają identyczną geometrię. Należy więc stworzyć tylko jednego "Parta". W początkowej chwili czasu zakładamy, że klocki idealnie przylegają do fragmentu tarczy i znajdują się na jej początku tak jak to przedstawiono na rysunku.
Materiał
Klocek jak i tarcza wykonane są z tego samego materiału o parametrach według poniższej tabeli.
| Stała materiałowa | Wartość |
|---|---|
| Young's modulus E [Pa] | $2200 \times 10^6 $ |
| Poisson's ratio [-] | $0.25$ |
| Density [kg/m$^3$] | $1550$ |
| Thermal expansion coefficient $1/K$ | $10\times 10^{-6}$ |
| Thermal conductivity [W/(m $\cdot$ K)] | $0.5$ |
| Specific heat [J/(kg $\cdot$ K)] | $1200$ |
Analiza
Symulację procesu należy wykonać używając kroku Dynamic, Temp-disp Explicit. Przyjąć czas trwania procesu równy 0.01 s.
Kontakt
Przyjąć model kontaktu z tarciem o współczynniku tarcia równym $0.33$. W okienku tworzenia własności kontaktu ("Edit Contact Property") wybieramy "Thermal->Heat Generation" i akceptujemy domyślne wartości. Dodatkowo wybieramy również "Thermal->Thermal Conductance". W okienku zaznaczamy opcję Use only pressure-dependency data i definiujemy następującą tabelę
| Conductance | Pressure |
|---|---|
| 50000 | 0 |
| 50000 | 1000 |
Warunki brzegowe
• Fragment tarczy ma zadane początkowe pole prędkości Create Predefined Field $v$, które powoduję przesuw tarczy w kierunku osi $z$.
• do obydwu klocków hamulcowych przyłożone jest ciśnineie $p$ powodujące docisk klocków do tarczy Create Load - > Pressure.
Siatka MES
Z uwagi na bardzo prostą geometrię należy wygenerować siatkę w oparciu o domyślne ustawienia proponowane przez program. Dla wszystkich ciała należy użyć element skończony C3D8T. Aby wybrać taki element klikamy w module Mesh opcję Assign Element Type. Z okienka wybieramy "Element Library: Explicit", "Family: Coupled Temperature-Displacement", "Geometric Order: Linear".
Ustawienie stałych fizycznych
Z menu wybieramy "Model->Edit Attributes->Model-1", gdzie "Model-1" to nazwa naszego modelu. Zaznaczamy opcję Absolute zero temperature i przypisujemy jej wartość $-273$ $^{\circ}$C. Zaznaczamy również opcję Stefan-Boltzmann constant i wprowadzamy wartość $5.67 \times 10^{-8}$ J/(s m$^2$ K$^4$).
Wymiana ciepła z otoczeniem
W analizowanym procesie uwzględniamy dwa mechanizmy wymiany ciepła z otoczeniem.
• Konwekcja, w module Interaction klikamy Create Interaction. Z listy wybieramy Surface film condition. Zaznaczamy powierzchnie zewnętrzną ciał. Ustawiamy "Film coefficient: 0.1" oraz "Sink temperature: 20.0".
• Radiacja, w module Interaction klikamy Create Interaction. Z listy wybieramy Surface radiation. Zaznaczamy powierzchnie zewnętrzną ciał. Ustawiamy "Emissivity: 0.6" oraz "Ambient temperature: 20.0".