# Ćwiczenie
Niech równanie ruchu ciała odkształcalnego będzie następujące
$$x_1 = X_1 + t^2 X_2, \quad x_2 = X_2+ t^2X_1, x_3 = X_3$$Wyznacz: ścieżkę po której poruszą cię cząstka materialna $\X=(1,2,1)$
# Ćwiczenie
Dla deformacji ciała opisanej równaniami
$$x_1 = X_1 + \beta X_2, \quad x_2 = X_2, \quad x_3 = X_3$$wyznacz kąt zawarty między wektorami $\v$ i $\w$ w konfiguracji aktualnej które odpowiadają wersorom osi układu współrzędnych $\e_1$ i $\e_2$ w konfiguracji początkowej.
# Ćwiczenie
Niech deformacje ciała będzie opisana następującymi równaniami
$$x_1 = a_1(X_1 + 2X_2), \quad x_2 = a_2 X_2, \quad x_3 = a_3X_3$$gdzie $a_1$, $a_2$, $a_3$ są pewnymi stałymi. Obszar ciała zdefiniowany jest jak na rysunku (jednostkowy sześcian).
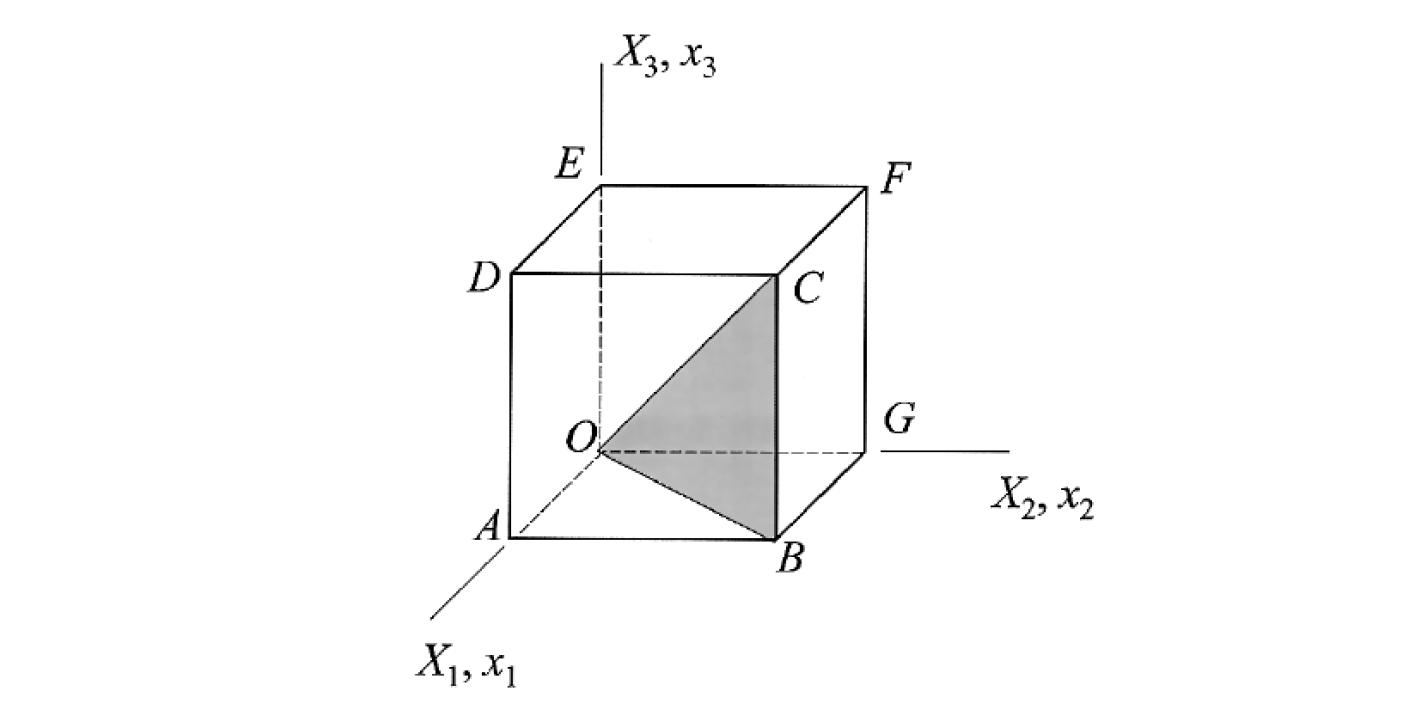
Wyznacz:
• długość przekątnej $OC$ po deformacji
• kąt między wektorami $OA$ i $OG$ po deformacji
• warunki jakie trzeba narzucić na stałe aby aby kąt wektorami $OC$ i $OB$ nie uległ zmianie podczas deformacji.
# Ćwiczenie
Show that an arbitrary homogeneous deformation can be decomposed into the product of a simple shear, a uniaxial extension normal to the plane of shear, a pure dilatation, and a rotation.
# Ćwiczenie
Show that an arbitrary homogeneous deformation can be decomposed into the product of three simple shears on mutually orthogonal planes, a pure dilatation, and a rotation.
# hr
# Ćwiczenie
Let a displacement field be given by
$$u_1 = \cfrac{1}{4}(X_3 - X_2), \qquad u_2 = \cfrac{1}{4}(X_1 - X_3), \qquad u_3 = \cfrac{1}{4}(X_2 - X_1)$$Determine the volume ratio $dV/dV_0$
# Ćwiczenie
Wyznacz objętość ciała po deformacji, jeżeli w konfiguracji początkowej jest sześcianem o boku $d$ zaś deformacja opisana jest następującymi równaniami:
$$x_1 = X_1 - X_2, \qquad \x_2 = \cfrac{1}{d^2}(X_1^3+X_2^3), \qquad x_3 = X_3$$ $$\Omega_0: \, 0 \leq X_1 \leq d, \quad 0 \leq X_2 \leq d, \qquad 0\leq X_3 \leq d$$# Ćwiczenie
Wyznacz pole powierzchni w konfiguracji aktualnej dla podstawy kwadratu z zadania wcześniej. Podstawa leży w płaszczyźnie $x_1-x_2$.