Wprowadzenie

Przepływ ciepła to proces wymiany energii cieplnej pomiędzy różnymi obszarami przestrzeni, wynikający z różnicy temperatur. Zrozumienie tego zjawiska jest kluczowe w budownictwie, szczególnie przy projektowaniu izolacji termicznej, ogrzewania oraz chłodzenia budynków.

Podstawowe równanie przewodzenia ciepła

Równanie przewodzenia ciepła w trzech wymiarach opisuje zależność temperatury od czasu i przestrzeni:

$$\frac{\partial T}{\partial t} = \alpha \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) + \frac{q}{\rho c_p}$$

gdzie:
• $ T(x, y, z, t) $ – temperatura $[K]$,
• $ \alpha = \frac{k}{\rho c_p} $ - dyfuzyjność cieplna $[m^2/s]$,
• $ k $ – współczynnik przewodzenia ciepła $[W/(m\cdot K)]$,
• $ \rho $ – gęstość materiału $[kg/m^3]$,
• $ c_p $ – ciepło właściwe materiału $[J/(kg \cdot K)]$,
• $ q $ – źródło (lub pochłaniacz) ciepła $[W/m^3]$.

Sposoby wymiany ciepła

• Przewodzenie: Transfer ciepła wewnątrz ciała stałego lub między ciałami stykającymi się.

$$\q = -k \frac{\partial T}{\partial \x}$$

• Konwekcja: Wymiana ciepła między ciałem stałym a płynem.

$$q_c = h (T_s - T_\infty)$$

• Promieniowanie: Wymiana ciepła w postaci fal elektromagnetycznych.

$$q_r = \varepsilon \sigma (T_s^4 - T_\infty^4)$$

gdzie $\varepsilon$ to emisyjność powierzchni, a $\sigma$ to stała Stefana-Boltzmanna.

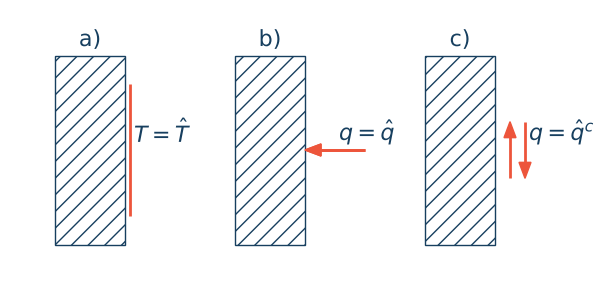
Warunki brzegowe

Równanie wymaga określenia warunków brzegowych:

• Warunki Dirichleta (stała temperatura na powierzchni):

$$T = \hat{T} \quad \text{na brzegu}$$

• Warunki Neumanna (zadany strumień ciepła):

$$-k \frac{\partial T}{\partial n} = q_n \quad \text{na brzegu}$$

• Warunki mieszane (konwekcja):

$$-k \frac{\partial T}{\partial n} = h (T - T_\infty) \quad \text{na brzegu}$$

gdzie $ h $ to współczynnik konwekcji $[W/(m^2 \cdot K)]$, a $ T_\infty $ to temperatura otoczenia.

Redukcja zagadnienia przepływu ciepła do 2D i 1D

Uproszczenie dla płaskiego problemu:

$$\frac{\partial T}{\partial t} = \alpha \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right) + \frac{q}{\rho c_p}$$

Równanie dla przepływu wzdłuż jednej osi (np. przewód cieplny):

$$\frac{\partial T}{\partial t} = \alpha \frac{\partial^2 T}{\partial x^2} + \frac{q}{\rho c_p}$$

Przykład obliczeniowy

Rozważmy przepływ ciepła w jednowymiarowej ścianie o gruboścu $ w= 0.1 $ m z warunkami:

$$T(0) = -10 \,^\circ \mathrm{C}, \quad T(w) = 20 \,^\circ \mathrm{C}$$

Równanie rożniczkowe opisujące to zagadnienie jest następujące

$$\frac{d^2 T}{dx^2} = 0$$

Rozwiązanie:

$$T(x) = C_1 x + C_2$$

Warunki brzegowe:

$$T(0) = -10 \rightarrow C_2 = -10$$ $$T(w=0.1) = 20 \rightarrow C_1 = 300$$

Poszukiwana funkcja

$$T(x) = 300x -10$$

Sprzężenia termo-mechaniczne

• równanie konstytutywne: (i) stałe materiałowe, szczególnie w plastyczności i lepko-sprężystości, mogą zależeć od temperatury, (ii) zmiany temperatury powodują dodatkowe odkształcenia (rozszerzalność cieplna); przy dużych zmianach temperatury wpływa to na rozwiązanie zagadnienia mechaniki.
• równanie przewodnictwa: określone jest na aktualnej geometrii, która jest funkcją pola przemieszczeń -- przy dużych deformacjach wpływa to na rozwiązanie tego równania
• nieodwracalne procesy w materiale (plastyczność, lepkość), które powodują dysypację energii, generują tym samym ciepło, a więc w r-niu przewodnictwa

Rozszerzalność cieplna

Kiedy materiał podlega zmianie temperatury, rozszerza się lub kurczy. Wielkość rozszerzenia lub kurczenia jest zazwyczaj charakteryzowana przez tensor rozszerzalność cieplnej $\a$, który jest miarą zmiany długości w danym kierunku przy zmianie temperatury o $1^{\circ}C$. Dla ciała bez naprężeń deformacje powstałą w wyniku zmiany temperatury możemy opisać jako

$$\F^{(T)} = \I+\a \Delta T$$

gdzie $\Delta T$ to temperatura względna (różnica między temperaturą rzeczywistą a temperaturą odniesienia, przy której $\F^{(T)} = \I$).

Jeżeli materiał jest izotropowy pod względem termicznym to wtedy tensor rozszerzalności cieplnej możemy wyrazić jako tensor kulisty tj. $\quad \a=a\I$, gdzie $a$ to współczynnik rozszerzalności cieplnej. Gradient deformacji dla takiego materiału wyraża się następująco

$$\F^{(T)} = (1+a \Delta T)\I$$

Dla małych deformacji mamy

$$\varepsilon_{ij} = \varepsilon^{(T)}_{ij} + \varepsilon^{(\sigma)}_{ij}$$

Wprzypadku liniowej sprężystości i małych deformacji związek konstytutywny możemy zapisać jako

$$\ss= \C\ee^{(\sigma)}= \C\cdot(\ee-\a T) = \C\cdot\ee - \C\cdot\a T$$

Odwrotne prawo mażemy zapisać następująco

$$\ee = \D\cdot\ss + \a T, \qquad \D = \C^{-1}.$$

Jeżeli warunki brzegowe uniemożliwiają powstanie odkształceń, to podgrzanie materiału do $T$ spowoduje powstanie naprężeń
$$\sigma_{11}=\sigma_{22}=\sigma_{33} = -\frac{EaT}{1-2\nu} = -3K\,aT$$

gdzie $K = \cfrac{E}{3(1-2\nu)}$ to moduł ściśliwości. Pozostałe składowe tensora naprężenia są równe zero, ($\sigma_{12}=\sigma_{23}=\sigma_{13}=0$). Zwróćmy uwagę na znak "$-$" oraz że dla $\nu=\frac12$ (materiał nieściśliwy) naprężenia będą nieskończenie wielkie.