Siły przekrojowe w płytach

Naprężenia normalne i styczne można rozłożyć wtedy na:
• symetryczną składową stałą
• antysymetryczną składową zmienną liniowo

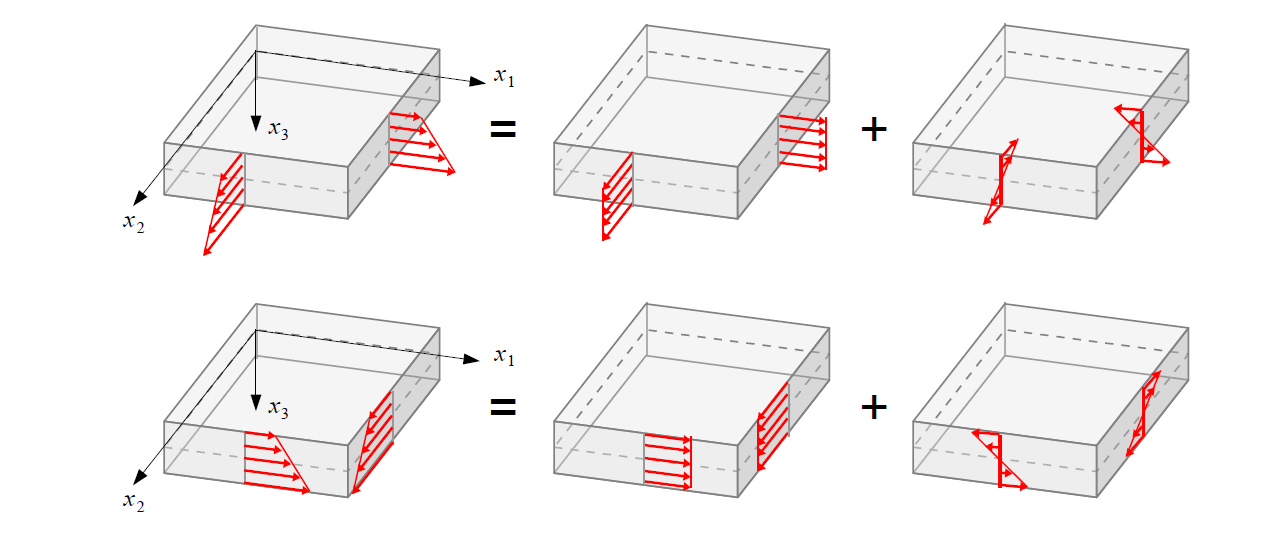
siła podłużna – suma symetrycznej części naprężeń normalnych

siła styczna – suma symetrycznej części naprężeń stycznych

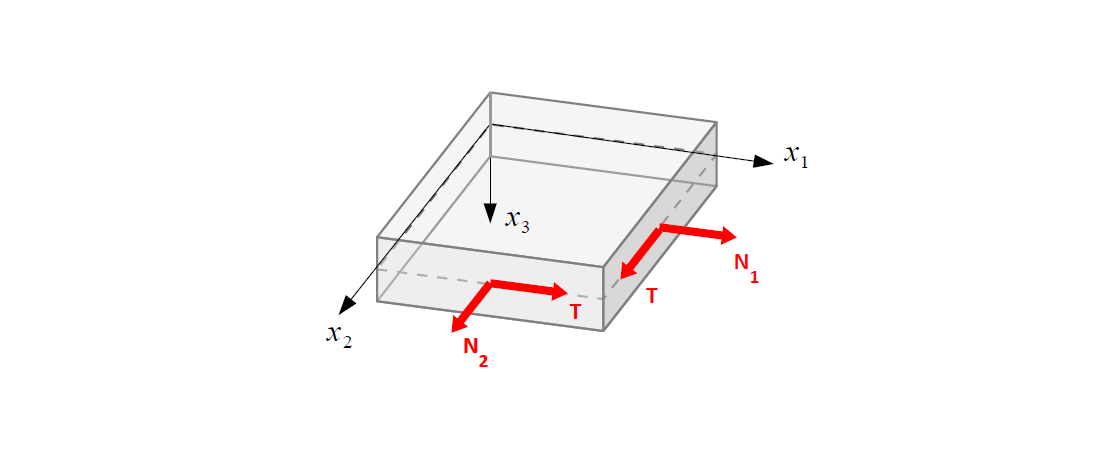
Wymiar fizyczny sił podłużnych i stycznych to $N/m$ – jest to liniowa gęstość sił odniesionych do przekroju poprzecznego o jednostkowej szerokości.

$$N_1 = \int_{-h/2}^{h/2} \sigma_{11} dx_3 = \cfrac{Eh}{1-\nu^2}\left( \pp{u}{x_1}+\nu \pp{v}{x_2}\right)$$ $$N_2 = \int_{-h/2}^{h/2} \sigma_{22} dx_3 = \cfrac{Eh}{1-\nu^2}\left( \pp{v}{x_2}+\nu \pp{u}{x_1}\right)$$ $$T = \int_{-h/2}^{h/2} \sigma_{12} dx_3 = \cfrac{Eh}{1-\nu^2}\cfrac{1-\nu}{2}\left( \pp{u}{x_2}+\pp{v}{x_1}\right)$$

Moment zginający – moment antysymetrycznej części naprężeń normalnych względem punktu na powierzchni środkowej.

Moment skręcający – moment antysymetrycznej części naprężeń stycznych względem punktu na powierzchni środkowej.

$$M_{11}= \int_{-h/2}^{h/2} x_3 \sigma_{11} dx_3 = -\cfrac{Eh^3}{12(1-\nu^2)}\left( \pp{^2w}{x_1^2}+ \nu\pp{^2w}{x_2^2}\right)$$ $$M_{22}= \int_{-h/2}^{h/2} x_3 \sigma_{22} dx_3 = -\cfrac{Eh^3}{12(1-\nu^2)}\left( \pp{^2w}{x_2^2}+ \nu\pp{^2w}{x_1^2}\right)$$ $$M_{12}= \int_{-h/2}^{h/2} x_3 \sigma_{12} dx_3 = -(1-\nu)\cfrac{Eh^3}{12(1-\nu^2)}\left( \pp{^2w}{x_1 \partial x_2}\right)$$

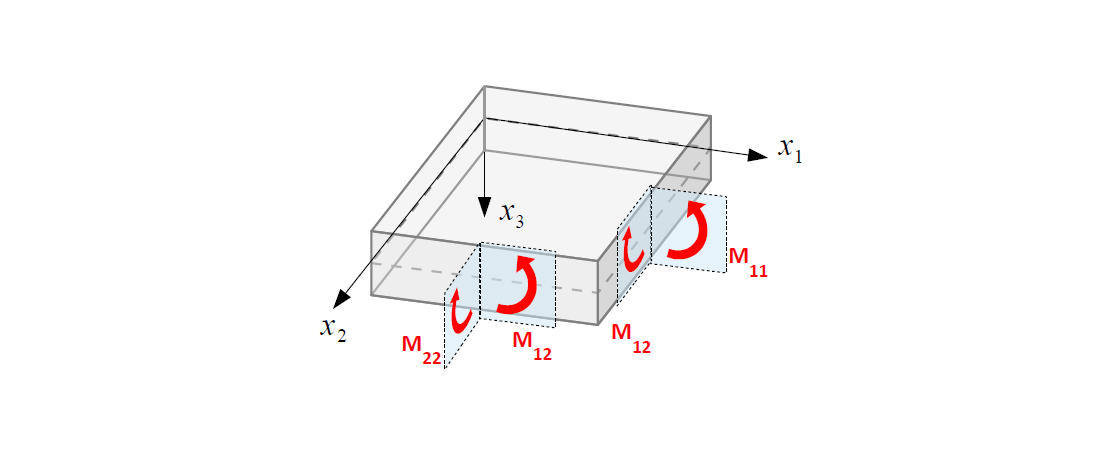
Siły poprzeczne warunki rownowagi

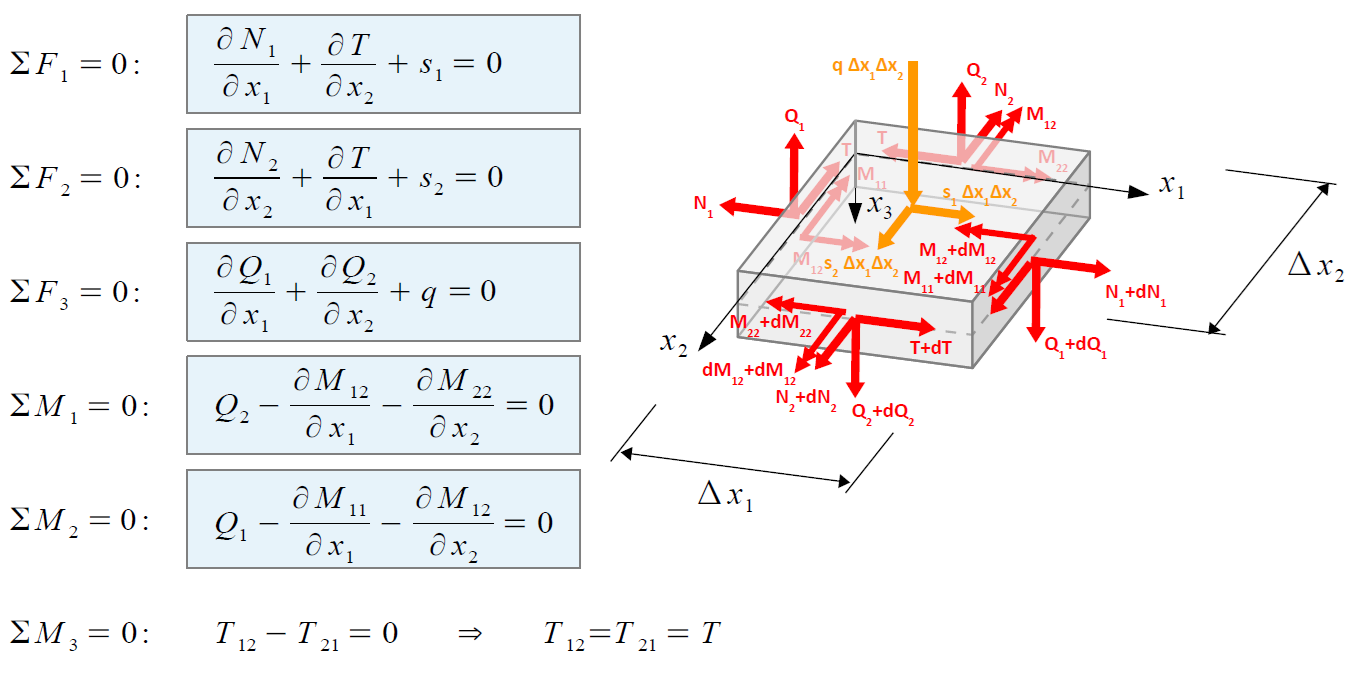
Równania rownowagi dla momentu staja sie definicja sil poprzecznych

$$Q_1 = \pp{M_{11}}{x_1} + \pp{M_{12}}{x_2}$$ $$Q_1 = \pp{M_{12}}{x_1} + \pp{M_{22}}{x_2}$$

Wymiar fizyczny momentów zginających i skręcających to $Nm/m$ – jest to liniowa gęstość momentów odniesionych do przekroju poprzecznego o jednostkowej szerokości.

Warunki brzegowe dla płyt

• pełne utwierdzenie, przemieszczenie i kąt obrotu równe zero
• swobodne podparcie - przemieszczenie rowne zero i moment zginajacy rowny zero
• wolny brzeg - moment i siła tnąca równa zero.

---

# Przykład

Rozważmy prostokątną cienką płytę $a \times b$ ($a = 2 \, \text{m}, b = 1 \, \text{m}$), swobodnie podpartą na wszystkich krawędziach. Płyta jest obciążona równomiernie rozłożonym obciążeniem $q = 1000 \, \text{N/m}^2$. Należy wyznaczyć:
• maksymalne ugięcie $w_{\text{max}}$,
• maksymalne momenty zginające $M_x$ i $M_y$.

Dane:
• grubość płyty $h = 0.1 \, \text{m}$
• moduł Younga $E = 210 \, \text{GPa}$
• współczynnik Poissona $\nu = 0.3$

Rozwiązanie

Sztywność zginania płyty $D = \frac{E h^3}{12 (1 - \nu^2)}$.

Podstawiamy dane:

$$D = \frac{210 \times 10^9 \cdot (0.01)^3}{12 \cdot (1 - 0.3^2)} = \frac{210 \cdot 10^{-6}}{12 \cdot 0.91} \approx 19.23 \, \text{Nm}.$$

Równanie równowagi (operator biharmoniczny):

$$\nabla^4 w = \frac{q}{D}, \quad \nabla^4 = \frac{\partial^4}{\partial x^4} + 2 \frac{\partial^4}{\partial x^2 \partial y^2} + \frac{\partial^4}{\partial y^4}.$$

Zakładamy rozwiązanie w postaci trygonometrycznej:

$$w(x, y) = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} W_{mn} \sin\left(\frac{m \pi x}{a}\right) \sin\left(\frac{n \pi y}{b}\right),$$

gdzie współczynniki $W_{mn}$ oblicza się jako:

$$W_{mn} = \frac{4 q}{\pi^4 D} \cdot \frac{1}{\left(\frac{m^2}{a^2} + \frac{n^2}{b^2}\right)^2}.$$

Maksymalne ugięcie $w_{\text{max}}$. Maksymalne ugięcie występuje w środku płyty $x = a/2, y = b/2$. Przyjmując pierwsze wyrazy szeregu ($m = 1, \, n = 1$), wyznaczamy:

$$w_{\text{max}} \approx \frac{4 q}{\pi^4 D} \cdot \frac{1}{\left(\frac{1^2}{a^2} + \frac{1^2}{b^2}\right)^2}.$$

Podstawiamy dane:

$$w_{\text{max}} \approx \frac{4 \cdot 1000}{\pi^4 \cdot 19.23} \cdot \frac{1}{\left(\frac{1}{2^2} + \frac{1}{1^2}\right)^2}.$$ $$w_{\text{max}} \approx \frac{4000}{19.23 \cdot 97.41} \cdot \frac{1}{1.5625^2}.$$ $$w_{\text{max}} \approx 0.013 \, \text{m} \, = \, 13 \, \text{mm}.$$

Moment zginający $M_x$ i $M_y$

Moment zginający \(M_x\) w środku płyty jest wyrażony wzorem:

$$M_x = -D \left( \frac{\partial^2 w}{\partial x^2} + \nu \frac{\partial^2 w}{\partial y^2} \right).$$

Obliczamy drugie pochodne:

$$\frac{\partial^2 w}{\partial x^2} = -\frac{\pi^2}{a^2} W_{11} \sin\left(\frac{\pi x}{a}\right) \sin\left(\frac{\pi y}{b}\right),$$ $$\frac{\partial^2 w}{\partial y^2} = -\frac{\pi^2}{b^2} W_{11} \sin\left(\frac{\pi x}{a}\right) \sin\left(\frac{\pi y}{b}\right).$$

W środku płyty ($x = a/2, y = b/2 $) mamy:

$$M_x = -D \left( -\frac{\pi^2}{a^2} W_{11} - \nu \frac{\pi^2}{b^2} W_{11} \right).$$

Podstawiamy dane:

$$M_x = 19.23 \cdot \pi^2 \cdot \frac{4 \cdot 1000}{\pi^4 \cdot 19.23} \cdot \frac{\left(\frac{1}{4} + 0.3 \cdot 1\right)}{\left(\frac{1}{4} + 1\right)^2}.$$

Po obliczeniach:

$$M_x \approx 61.2 \, \text{Nm/m}.$$

Analogicznie dla \(M_y\):

$$M_y = -D \left( \nu \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} \right).$$ $$M_y \approx 30.6 \, \text{Nm/m}.$$

---