Wprowadzenie
Prętem cienkościennym prostym nazywamy pręt którego jeden z wymiarów określających przekrój poprzeczny jest nieporównywanie mniejszy w stosunku do drugiego zaś wszystkie tworzące są równoległe do jego osi.
Praktyka pokazuje, że pręt możemy uznać za cienkościenny jeżeli grubość ścianki $\delta$ jest co najmniej ośmiokrotnie mniejsza niż najdłuższa droga $c$ mierzona po linii środkowej oraz jeżeli droga ta jest ośmiokrotnie mniejsza od długości pręta $l$
$$\delta \leq \cfrac18, \qquad c \leq \cfrac18l$$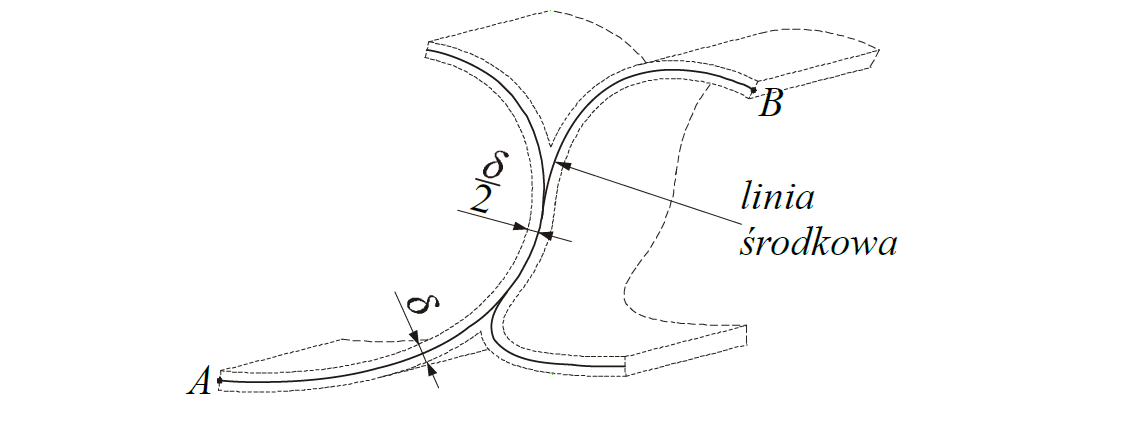
Z uwagi na geometrię przekroju pręta wyróżniać będziemy pręty cienkościenne
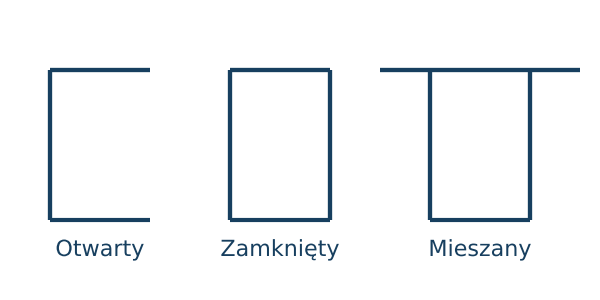
• otwarte - czyli takie których linię środkową możemy opisać grafem drzewa
• zamknięte - czyli takie których linę środkową możemy opisać grafem złożonym wyłącznie z obwodów
• mieszane - czyli takie których linę środkową opisuje graf spójny, planarny, zawierający obwody
Układ odniesienia
W odniesieniu do analizy prętów cienkościennych rozważamy 3 typy układów
• globalny $(X,Y,Z)$ w którym oś $X$ jest równoległa do osi pręta prostego. Układ ten służy do wyznaczania położenia osi głównych centralnych pręta.
• centralny $(x,y, z)$ w którym oś $x$ jest osią pręta, zaś osie $y$ oraz $z$ są osiami głównymi centralnymi przekroju poprzecznego. Układ ten służy do opisu linii środkowej
• lokalny $(x, s, n)$ krzywoliniowy układ ortogonalny którego pierwsza oś jest równoległa do osi $x$, druga oś jest styczna do linii środkowej a trzecia wyznacza wektor prostopadły to pierwszych dwóch osi.
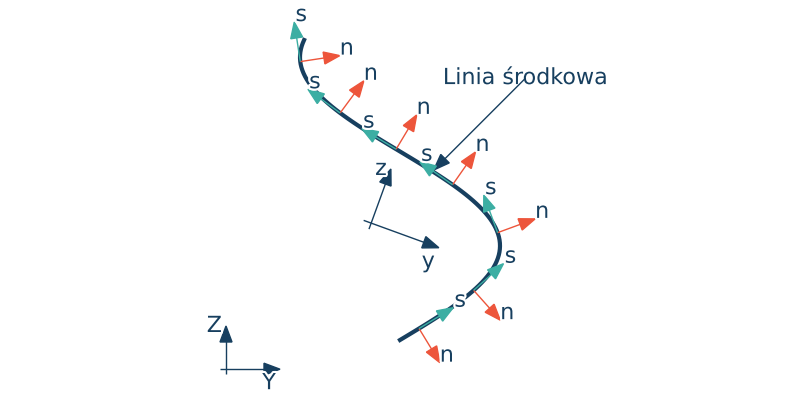
Współrzędna wycinkowa
Zapiszmy współrzędne wersorów lokalnego układu współrzędnych w dowolnym punkcie $M(s)$ odniesione do ukłądu centralnego $(x,y,z)$
$$\e_s = [\dot{y}(s), \,\,\dot{z}(s)], \quad \e_n = [ -\dot{z}(s), \,\, \dot{y}(s)]$$gdzie $\dot{(\cdot)}$ oznacza pochodną względnej zmiennej $s$. W dowolnym miejscu płaszczyzny przekroju poprzecznego przyjmijmy punkt (biegun) $B(y_B, z_B)$. Biorą dowolny punkt $M(s)$ o wektorze wodzącym $\boldsymbol{\rho} (s)$ zaczepionym w biegunie $B$ obliczmy następującą wartość
$$d\omega_B(s) = \boldsymbol{\rho}(s) \cdot \e_n(s) ds$$Całkując powyższy wzór dostajemy definicję współrzędnej wycinkowej
$$\omega_B(s) = \int_0^s \boldsymbol{\rho}(s) \cdot \e_n(s) ds$$Powyższy wzór można również zapisać w układzie lokalnym. Współrzędne wektorów w tym układzie są następujące
$$\e_n = [0, 1], \qquad \boldsymbol{\rho} = [\rho_s(s), \,\, \rho_n(s)]$$co pozwala zapisać wartość współrzędnej wycinkowej jako
$$\omega_B = \int_0^s \rho_n(s) ds$$Wartość wycinkowej współrzędnej zależy zarówno od położenia bieguna jak i od punktu który określa początek współrzędnej wycinkowej.
# Przykład
Napisać i narysować funkcje współrzędnej wycinkowej dla kątownika jak na rysunku.
• dla marszruty 1
$$0 \leq s \leq a: \qquad \omega_B(s) = \int_0^s bds = bs$$• dla marszurty 2
$$0 \leq s \leq b: \qquad \omega_B(s) = \int_0^s (-a)ds = -as$$Dodatnie wartości $\omega(s)$ będziemy odkładać po dodatniej stronie osi $n$.
Charakterystyki wycinkowe
Niektóre z całek po dendrycie $d$ oznaczać będziemy następującymi symbolami
• wycinkowy moment statyczny
$$S_{\omega} = \int_d \omega(s)\delta(s) ds$$• wycinkowe momenty odśrodkowe
$$I_{\omega y} = \int_d \omega(s)y(s)\delta(s) ds$$ $$I_{\omega z} = \int_d \omega(s)z(s)\delta(s) ds$$• wycinkowy moment bezwładności
$$I_{\omega} = \int_d \omega^2(s)\delta(s) ds$$Charakterystyki geometryczne
Znane charakterystyki dla prętów litych moją nieco inną definicję dla prętów cienkościennych
• moment statyczny względem osi $y$
$$S_y = \int_d z(s)\delta(s)ds$$• moment odśrodkowy
$$S_{yz} = \int_d y(s) z(s)\delta(s)ds$$• moment bezwładności względem osi $y$
$$I_{y} = \int_d z^2(s)\delta(s)ds$$Wartości obliczone według powyższych wzorów różnią się pomijanie mało od wartości obliczonych w sposób klasyczny.
Środek zginania
W układzie osi centralnych oznaczmy położenie bieguna i początku współrzędnej łukowej. Obliczmy w tym układzie wartości $I_{\omega y}$ oraz $I_{\omega z}$
Jeżeli dobierzemy położenie bieguna w taki sposób aby moment odśrodkowe były równe 0 to taki punkt nazywamy środkiem zginania.
$$y_R = -\cfrac{I_{\omega z}}{I_y} + y_B, \qquad z_R = -\cfrac{I_{\omega y}}{I_z} + z_B$$# Przykład
Wyznacz położenie środka zginania dla profilu ceowego jak na rysunku. Grubość ścianki wynosi $\delta=0.1cm$ a pozostałe wymiary odpowiednio $h=6cm$ i $f=3cm$.
Początek globalnego układu współrzędnych został przyjęty w punkcie $O$ który jest zarazem biegunem jak również początkiem współrzędnej łukowej $s$.
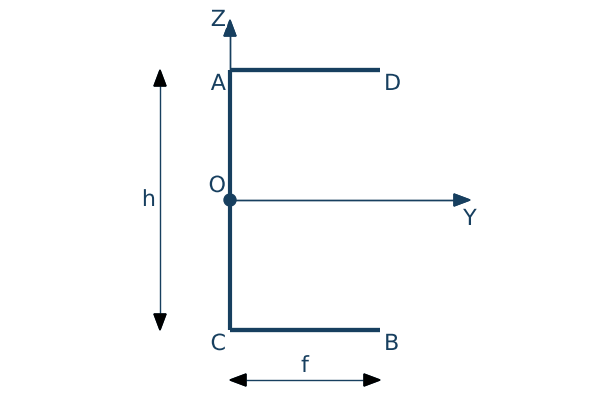
• wyznaczenie charakterystyk geometrycznych (układ globalny)
pole przekroju
$$A = 2 \int_{0}^{s_A} \delta ds + 2 \int_{s_A}^{s_B}\delta ds \Rightarrow 1.2 \cdot 10^{-4} m^2$$• wyznaczenie środka ciężkości
$$a_s = \cfrac{S_z}{A}, \quad S_z = 2\int_{s_A}^{s_B}(s-3 \cdot 10^{-2})\delta \,ds, \quad a_s = 0.0075$$Znając położenie środka ciężkości możemy wyznaczyć układ osi głównych centralnych i obliczyć względem nich momenty bezwładności
$$z_1(s) = 3 \cdot 10^{-2}, \quad z_2(s) = s$$ $$I_y = 2 \int_{s_A}^{s_B} [z_1(s)]^2 \delta \, ds + 2 \int_{s_O}^{s_A} [z_2(s) ]^2\delta \, ds = 7.2 \cdot 10^{-8} m^4$$ $$y_1(s) = s - 3 \cdot 10^{-2} - a_s \quad y_2(s) = -a_s$$ $$I_z = 2 \int_{s_A}^{s_B} [y_1(s)]^2 \delta \, ds + 2 \int_{s_O}^{s_A} [y_2(s) ]^2\delta \, ds = 1.125 \cdot 10^{-8} m^4$$• funkcje wycinkowej współrzędnej