Wprowadzenie

Model belki Timoszenki jest rozszerzeniem klasycznego modelu Eulera-Bernoulliego, który uwzględnia dodatkowe efekty związane z naprężeniami stycznymi i odkształceniami postaciowymi. Został on zaproponowany przez Stefana Timoszenkę w pierwszej połowie XX wieku i jest stosowany do analizy zachowania belek, szczególnie w sytuacjach, gdzie założenia modelu Eulera-Bernoulliego nie są wystarczające.

Podstawowe założenia modelu:

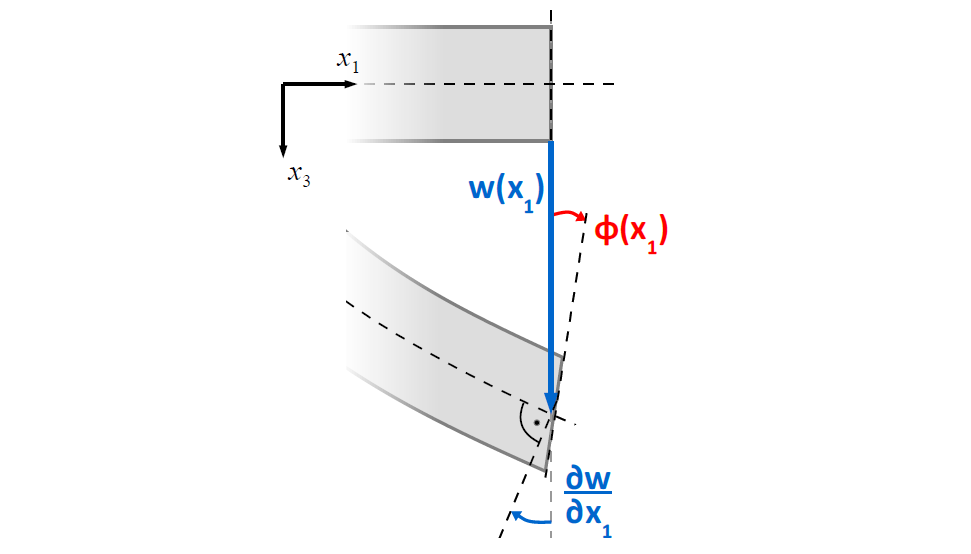
• Ugięcie i rotacja przekroju: Przekrój poprzeczny belki po deformacji może nie być prostopadły do zdeformowanej osi belki. W modelu Timoszenki zakłada się, że przekrój może obracać się o pewien kąt $\phi$, co oznacza, że nie pozostaje on prostopadły do osi neutralnej, ale nadal zachowuje swoją płaskość.

• Uwzględnienie naprężeń stycznych: Model uwzględnia wpływ naprężeń stycznych na deformację belki, co pozwala na dokładniejszą analizę, szczególnie w przypadku krótkich i grubościennych belek, gdzie naprężenia styczne odgrywają znaczącą rolę.

• Małe odkształcenia: Podobnie jak w modelu Eulera-Bernoulliego, odkształcenia są uważane za na tyle małe, że można je analizować przy pomocy liniowej teorii sprężystości.

• Jednorodność materiału: Materiał belki jest jednorodny i izotropowy, co oznacza, że jego właściwości mechaniczne są jednakowe we wszystkich kierunkach i punktach.

Model Timoszenki jest bardziej zaawansowanym narzędziem w analizie mechanicznej belek, szczególnie przydatnym w sytuacjach, gdzie uproszczenia modelu Eulera-Bernoulliego prowadzą do znacznych błędów, na przykład w przypadku krótkich belek, belek o dużej grubości lub przy analizie dynamicznej.

Deformacja belki Timoshenki.

Model matematyczny

Równania opisujące model belki Timoshenki są następujące

gdzie $q(x)$ to funkcja opisujące obciążenie belki, $E$ to moduł Younga, $G$ - moduł ścinania, $I$ moment bezwładności, $\kappa$ - współczynnik korekcyjny.

Jest to układ dwóch równań różniczkowych zwycznajnych na poszukiwane funkcje $w(x)$ - funkcja ugięcia oraz $\phi(x)$ - funkcja obrotu przekroju poprzecznego. Przedstawiony układ rówń trzeba uzupełnić o warunki brzegowe wynikające z obciązenia belki oraz podpór.

Współczynnik korekcyjny wyznaczany jest według wzoru

gdzie $A$ to pole przekroju poprzecznego belki, $I$ to moment bezwładności, $b(z)$ to szerokość przekroju, a $S(z)$ to moment statyczny. W przypadku przekroju prostokątnego wymienione parametry przyjmują następujące wartości:

Dla przekroju kołowego mamy

Siły przekrojowe wyznaczamy z następujących wzorów

Zastosowanie

• Belki krótkie i grube, gdzie efekty ścinania są znaczące.

# Przykład

Wyznacz wartość współczynnika korekcyjnego dla przekroju prostokątnego i kołowego.

from sympy import *
import numpy as np
x = Symbol('x')
z = Symbol('z')
b = Symbol("b")
h = Symbol("h")
A = b*h
I = b*h**3/12
S = b/2*(h**2/4-z**2)
e = integrate(S**2/b**2, (z, -h/2,h/2), (x, -b/2, b/2))
k = 1/(A/I**2*e)
print(k)
## przekoj kolowy - metoda monte carlo
R = 1
A = np.pi*R**2
I = np.pi*R**4/4
n = 10000
t = np.linspace(-R, R, n)[1:-1]
t = np.random.rand(n)[1:-1]*2*R-R
z, x = np.meshgrid(t,t)
b = 2*(R**2-z**2)**(1/2)
S = 2/3*(R**2-z**2)**(3/2)
f= S**2/b**2
d = np.sqrt(z**2+ x**2)
ind = d<R
avg = np.average(f[ind])
e = avg*np.pi*R**2
k = 1/(A/I**2*e)
print(k)

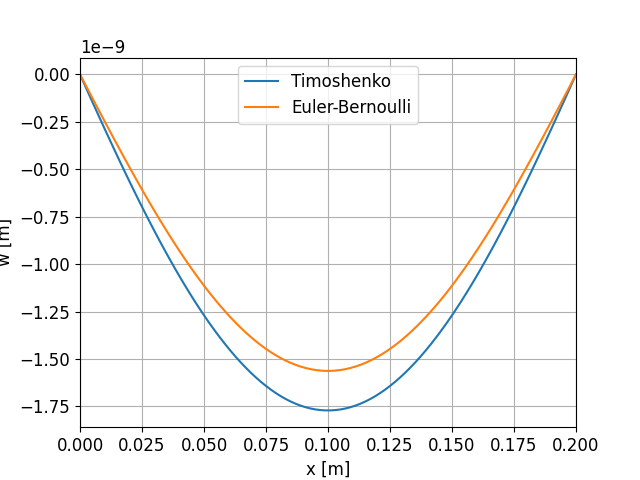
# Przykład

Oblicz ugięcie belki wolnopodpartej obciążonej w sposób ciągły wykorzystują teorię belek Timoshenki. Belka ma długość równą $L$, jej sztywność giętna wynosi $EI$, pole przekroju poprzecznego jest równe $A = b\times h$, moduł ścinania jest równy $G$, a współczynnik korekcyjny wynosi $\kappa$.

Funkcja ugięcia dla belki Timoshenki.