Wprowadzenie
Model belki Bernoulliego-Eulera jest klasycznym modelem opisującym zachowanie belek poddanych zginaniu. Jest szeroko stosowany w inżynierii do analizy ugięć, naprężeń oraz stabilności belek. Model ten opiera się na kilku podstawowych założeniach.
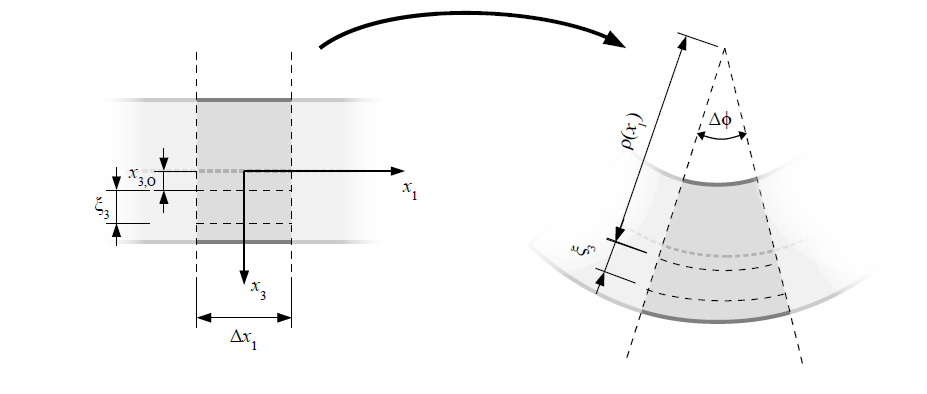
Hipoteza płaskich przekrojów
Przekroje poprzeczne belki przed i po deformacji pozostają płaskie i prostopadłe do osi belki. Oznacza to, że przekrój nie ulega odkształceniom ani obrotom względem siebie, co upraszcza analizę naprężeń i ugięć.
Model fizyczny
Model fizyczny opisujący belkę zakłada że belka jest prostoliniowa. Przekrój poprzeczny belki jest symetryczny względem osi neutralnej. Obciążenia działają w płaszczyźnie pionowej, co oznacza, że belka jest poddawana głównie zginaniu. Obciążenia mogą być rozłożone równomiernie lub skupione w określonych punktach. Belka może być podparta na różne sposoby, np. swobodnie podparta, utwierdzona na jednym końcu lub utwierdzona na obu końcach.
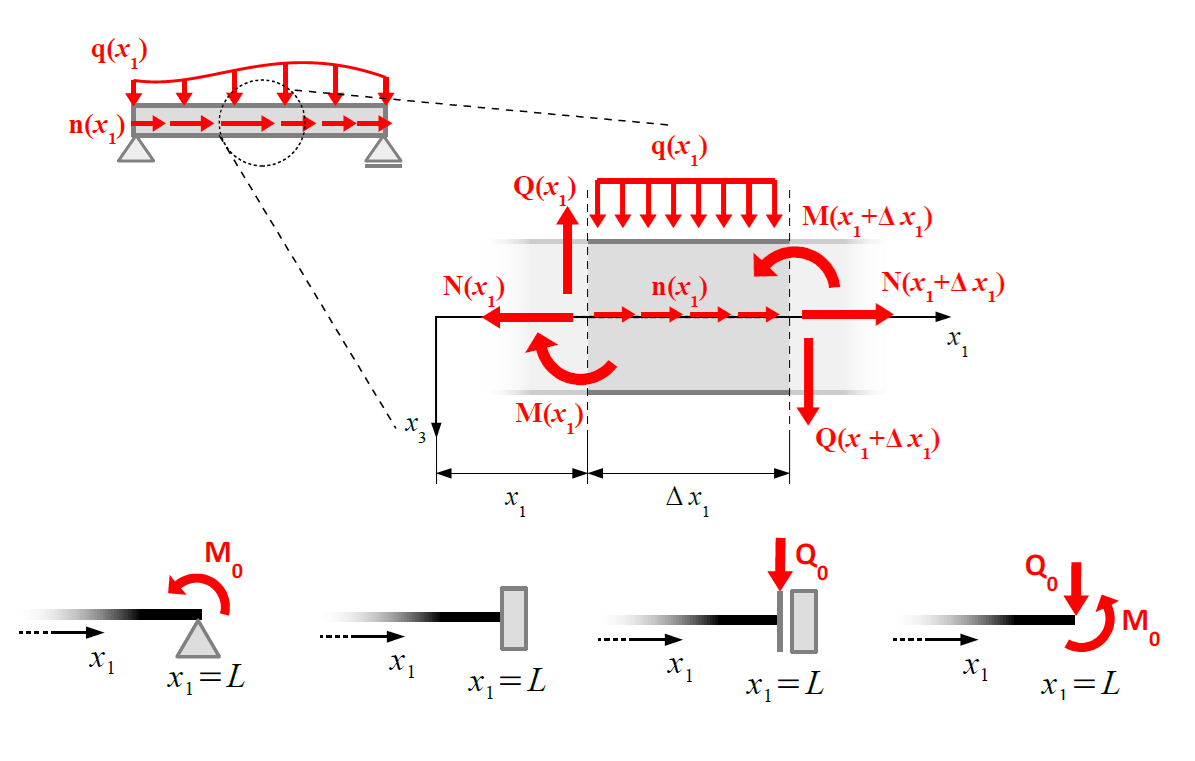
Model matematyczny
Równanie belki Bernoulliego-Eulera
$$\dd{^2}{x^2}\left[\ E I \dd{^2w(x)}{x^2}\right] = q(x),$$gdzie $q(x)$ to funkcja obciążenia ciągłego występująca na belce, $E$ to moduł Younga, $I$ to moment bezwładności przekroju poprzecznego belki.
Przedstawione równanie to niejednorodne, liniowe równanie różniczkowe zwyczajne czwartego rzędu. Model ten moża z powodzeniem stosować do belek o zmiennym przekroju czyli gdy sztywność giętna $E I$ jest funkcją $x$. Równanie Bernoulliego-Eulera wymaga czterech warunków brzegowych na ugięcie, kąt obrotu, moment zginający oraz siłę poprzeczną.
Kąt obrotu wyznaczamy poprzez różniczkowania funkcji ugięcia
$$\phi(x) = \dd{w(x)}{x}$$Moment zginający możemy wyrazić jako
$$M(x) = -E I \dd{^2w(x)}{x^2}$$a siłę poprzeczną jako
$$Q(x) = -EI \dd{^3w(x)}{x^3}$$Warunki brzegowe
Warunki brzegowe konstruujemy poprzez odpowiednie zapisanie znanych wartości ugięcia, kąta obrotu, momentu zginającego oraz siły poprzecznej dla różnych sposobów podparcia i obciążenia belki na jej końcach.
Rozważmy w pierwszej kolejności belkę wspornikową jak na rysunku. Warunki brzegowe dla tej belki będą następujące
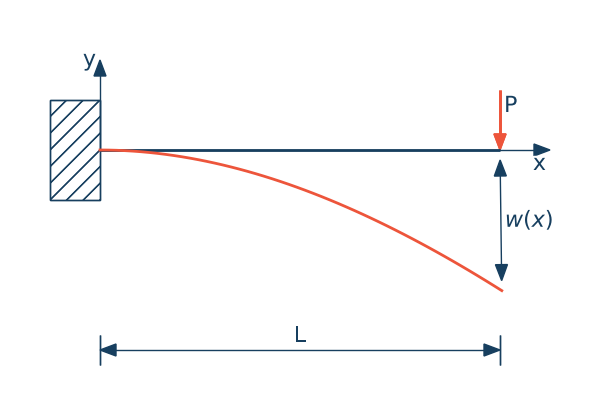
Dla belki swobodnie podpartej obciążonej w sposób ciągły warunki brzegowe będą następujące
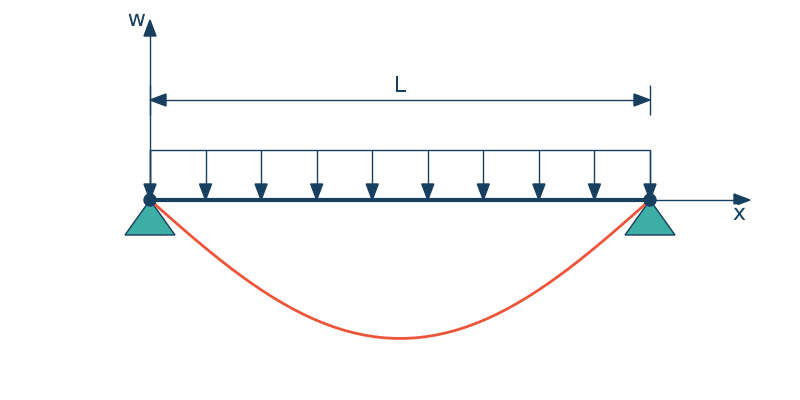
Rozkład siły poprzecznej oraz momentu zginającego możemy wyznaczyć rozwiązując następujące równanie różniczkowe
$$\dd{Q(x)}{x} = -q(x), \quad \dd{M(x)}{x} = Q(x)$$Są to wzory Schwedlera-Żurawskiego.
Zastosowanie
• Belki smukłe (gdzie stosunek długości do wysokości przekroju poprzecznego jest duży).
• Przy obciążeniach statycznych lub quasi-statycznych.
# Przykład
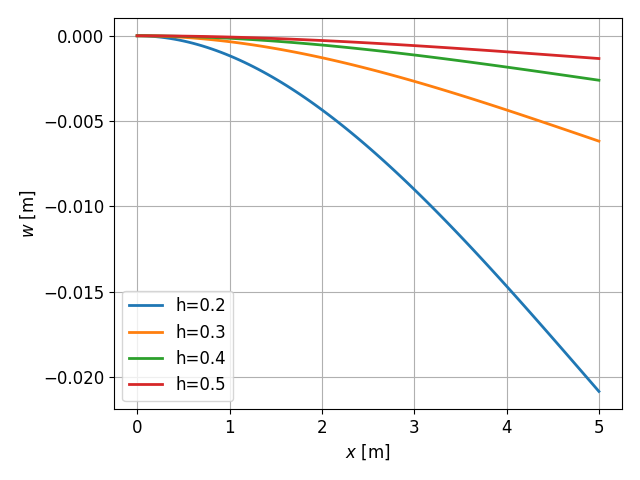
Znajdź rozwiązanie analityczne belki wspornikowej o długości $L$ obciążonej siłą skupioną o wartości $P$. Belka ma przekrój prostokątny o bokach: $b$ - szerokość i $h$ - wysokość.
$$EI\dd{^4w(x)}{x^4} = 0, \quad x \in (0, L)$$Warunki brzegowe:
$$w(x=0)=0, \quad \phi(x=0)=0, \quad M(x=L) = 0, \quad Q(x=L) = P$$Rozwiązanie
$$w(x) = \cfrac{-6L\,P\,x^2}{E\,b\,h^3} + \cfrac{2P\,x^3}{Ebh^3}$$from sympy import Function, dsolve, Derivative
from sympy import Symbol
x = Symbol("x")
L = Symbol("L")
b = Symbol("b")
h = Symbol("h")
E = Symbol("E")
P = Symbol("P")
I = b*h**3/12
w = Function('w')
fun = E*I*Derivative(Derivative(Derivative(Derivative(w(x), x),x),x))
r = dsolve(fun, ics={
w(0): 0, # ugięcie rowne zero
w(x).diff(x).subs(x, 0): 0, # kąt ugiecia
w(x).diff(x,2).subs(x, L): 0, # moment zginajacy
w(x).diff(x,3).subs(x, L): P/E/I # siła poprzeczna
})
print(r)