Ciało fizyczne odkształcalne
Ciało fizyczne to zbiór cząstek o niezerowej masie traktowany jako całość. Ciało odkształcalne to ciało fizyczne, w którym wzajemne odległości cząstek mogą ulegać zmianie pod wpływem działających na nie sił. W rzeczywistości wszystkie ciała fizyczne są odkształcalne!
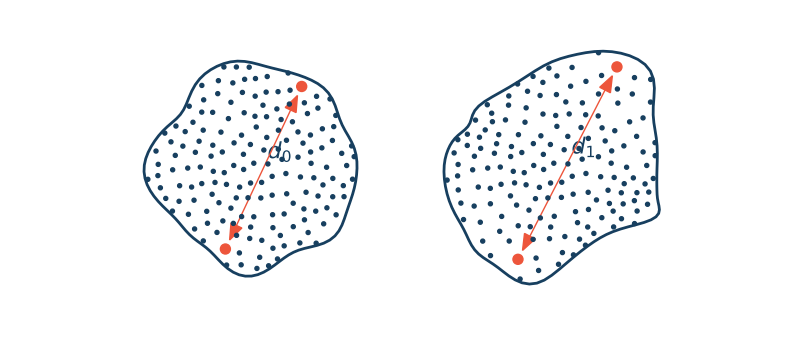
Wektor przemieszczenia
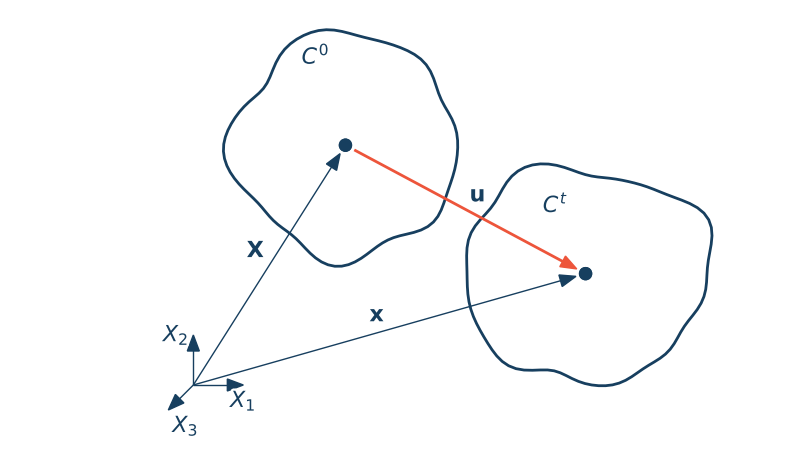
Przypiszmy dowolnemu punktowi $A$ współrzędne $\X = [X_1, X_2, X_3]$. Ten sam punkt po odkształceniu zmieni swoje położenie. Jego nowe współrzędne będą równe $\x = [x_1, x_2, x_3]$. Wektorom przemieszczenia punktu materialnego nazywamy wektor
$$\u = \x-\X, \quad [m]$$Jednostką przemieszenia w układzie SI jest metr. Wektor ten posiada trzy składowe których wartości zależą od przyjętego układu współrzędnych.
Gradient deformacji
$$\F = \pp{\x}{\X}, \, F_{ij} = \pp{x_i}{X_j}$$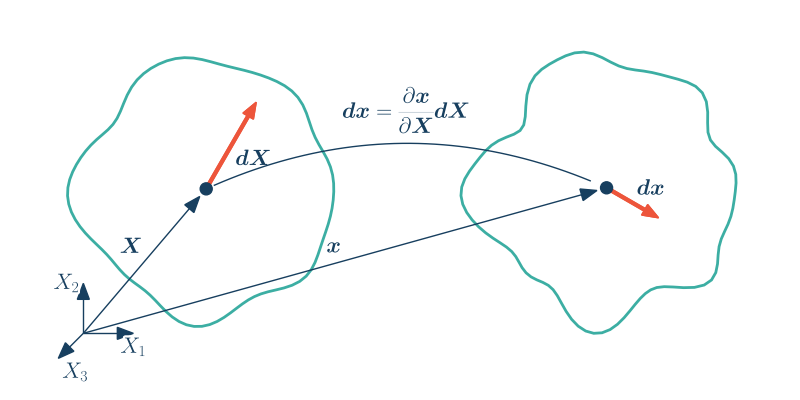
Gradient przemieszczenia
$$\H = \pp{\u}{\X}, \, H_{ij} = \pp{u_i}{X_j}$$Tensor deformacji
Oznaczmy długość infinitezymalnego włókna materialnego przed deformacją jako $dL$ oraz po deformacji jako $dl$. Kwadrat długość zdeformowanego włókna materialnego będzie wynosił
$$(dl)^2 = d\x\cdot d\x = dx_i dx_i =(F_{ij}dX_j)(F_{ik}d X_k) =dX_j(F_{ij}\:F_{ik})dX_k =dX_j\:C_{jk}\: d X_k = d \X \C d \X,$$gdzie tensor drugiego rzędu $\C$ jest nazywany tensorem deformacji i jest on dodatnio określony.
Tensor odkształcenia Greena
Rozważmy różnice kwadratów długości włókna przed i po deformacji. Oznaczmy te długości odpowiednio jako $dL$ - długość początkowa włókna, $dl$ - długość włókna po deformacji.
$$(dl)^2 - (dL)^2 = dx_idx_i -dX_jdX_j = (C_{jk}-\delta_{jk}) dX_jdX_k =2\cfrac{1}{2}(C_{jk}-\delta_{jk}) dX_jdX_k = 2 E_{jk} dX_jdX_k$$ $$\varepsilon^G_{ij} = \cfrac{1}{2}(C_{ij} - \delta_{ij}),\, \E = \cfrac{1}{2}(\C-\I)$$ $$ds-dS = \d\x \cdot \d\x - \d\X \cdot \d\X = \pp{x_k}{X_i}dX_i\pp{x_k}{X_j}dX_j - \delta_{ir}\delta_{jr}dX_i dX_j =$$ $$\left(\pp{x_k}{X_i}\pp{x_k}{X_j} -\delta_{ij} \right)dX_i dX_j$$ $$\varepsilon_{ij}^G = \cfrac12\left( \pp{u_i}{X_j} + \pp{u_j}{X_i} + \pp{u_k}{X_i}\pp{u_k}{X_j} \right)$$Związki geometryczne
Wykorzystując związek między $\F$ i $\H$ dla miar deformacji otrzymujemy następujące związk
$$\C = \F^T\F = (\H+\I)^T(\H+\I) = \H + \H^T + \H^T\H + \I$$W zapisie indeksowym wzory te wyrażają się następująco
$$C_{ij} = H_{ki}H_{kj} + H_{ij} + H_{ji} +\delta_{ij}$$Wykorzystując tak obliczone tensory deformacji możemy zapisać tensor odkształcenia jako
$$\ee^G = \cfrac{1}{2}(\H + \H^T + \H^T\H)$$Tensor małego odkształcenia
$$\ee = \cfrac{1}{2}(\H + \H^T)$$Interpretacja składowych tensora
• składowe normalne (składowe które leżą na przekątnej głównej tensora drugiego rzędu)
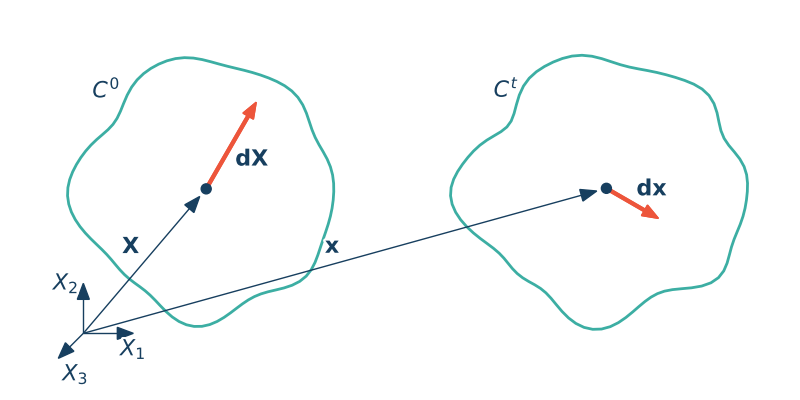
Wybierzmy włókno materialne $d\X$ w konfiguracji odniesienia oraz jego transformację w konfiguracji aktualnej $d\x$ tak aby jego kierunek był równy
$$\mathrm{d}\X = \mathrm{dL}\N, \qquad \mathrm{d}\x = \mathrm{dl}\n, \qquad |\N| = 1, \, |\n| = 1$$Wykorzystując definicję tensora deformacji $C$ kwadrat długości tego włókna wynosi
$$\mathrm{dl}^{2} = \mathrm{d}\X\C\mathrm{d}\X= \mathrm{dL}^{2} \N\C\N$$Wprowadźmy następującą definicję $\lambda = \cfrac{\mathrm{dl}}{\mathrm{dL}}$ wtedy
$$\lambda^{2} = \N\C\N$$Podstawmy za $\N=\e_1 \quad \Rightarrow \quad \lambda_1^{2} = \e_1 \C\e_1 = C_{11}$. Podobnie podstawiając pozostałe wektory bazowe dostajemy $\lambda_2^{2} = \e_2 \C\e_2 = C_{22}$ oraz $\lambda_3^{2} = \e_3 \C\e_3 = C_{33}$
$$\left[\begin{array}{ccc}1 & 0 & 0\\\end{array}\right] \left[ \begin{array}{ccc} C_{11} & C_{12} & C_{13}\\ & C_{22} & C_{23}\\ sym & & C_{33} \end{array}\right] \left[\begin{array}{c}1\\0\\0\\\end{array}\right]=C_{11}$$Składowe normalne tensora deformacji $\C$ są równe kwadratowi względnego rozciągnięcia włókien materialnych wzdłuż kierunków wyznaczonych przez wektory bazowe.
Jeżeli włókno nie uległo deformacji to składowe normalne są równe $1$. Maksymalne wydłużenia względne otrzymujemy dla włókien wzdłuż kierunków głównych $\C$.
• składowe styczne
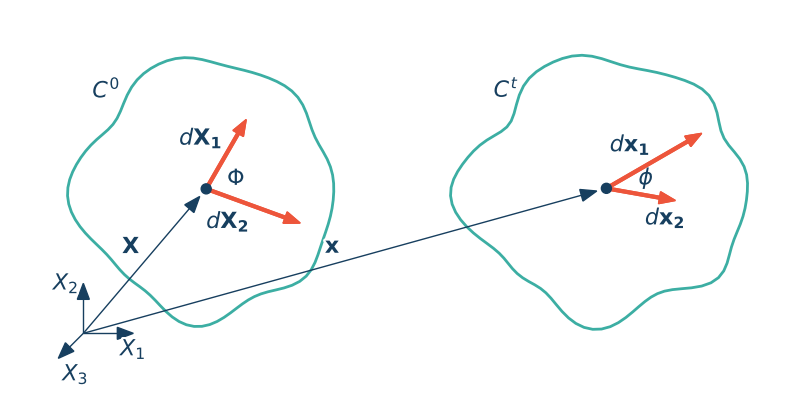
Wybierzmy dwa włókna materialne $d\X_1$ i $d\X_{2}$ w konfiguracji odniesienia oraz ich transformację w konfiguracji aktualnej $d\x_{1}$ i $\mathrm{d}\x_{2}$ tak aby
$$\mathrm{d}\X^{1} = \mathrm{dL_{1}}\N_{1}, \qquad \mathrm{d}\x_{1} = \mathrm{dl_{1}}\n_{1}, \qquad |\N_{1}| = 1, \, |\n_{1}| = 1$$ $$\mathrm{d}\X_{2} = \mathrm{dL_{2}}\N_{2}, \qquad \mathrm{d}\x_{2} = \mathrm{dl_{2}}\n_{2}, \qquad |\N_{2}| = 1, \, |\n_{2}| = 1$$Obliczmy cosinus kąta między włóknami w konfiguracji początkowej i aktualnej. Wykorzystując wektory jednostkowe kąt ten w konfiguracji początkowej wynosi
$$\cos(\Phi) = \N_{1}\N_{2},$$natomiast w konfiguracji aktualnej wykorzystując definicję tensora deformacji dostajemy
$$\cos(\phi) = \n_{1}\n_{2} = \cfrac{1}{\mathrm{dl}_{1}\mathrm{dl}_{2}}\mathrm{d}\x_{1} \mathrm{d}\x_{2} = \cfrac{1}{\mathrm{dl}_{1}\mathrm{dl}_{2}}(\F \mathrm{d}\X_{1}) (\F \mathrm{d}\X_{2}) =$$ $$\cfrac{\mathrm{dL}_{1}\mathrm{dL}_{2}}{\mathrm{dl}_{1}\mathrm{dl}_{2}}(\F \N_{1}) (\F \N_{2}) = \cfrac{1}{\lambda_{1} \lambda_{2}} \N_{1}\C\N_{2}.$$Zmianę kąta między włóknami w wyniku deformacji (kąt odkształcenia postaciowego) możemy zapisać jako
$$\gamma = \Phi - \phi$$Podstawmy za $\N_{1}=\e_1,\ \N_{2} = \e_2$ wtedy
$$\cos(\Phi) = \e_1\e_2=0 \rightarrow \Phi=\cfrac{\pi}{2}, \,\, \cos(\phi) = \cfrac{1}{\lambda_{1} \lambda_{2}} \e_1\C\e_2 = \cfrac{C_{12}}{\sqrt{C_{11}}\sqrt{C_{22}}}$$Policzmy sinus kąta $\gamma$: $\sin(\gamma) = \sin(\pi/2 - \phi) = \cos(\phi)$
Ostatecznie dostajemy
$$\sin(\gamma_{12}) = \cfrac{C_{12}}{\sqrt{C_{11}}\sqrt{C_{22}}}$$W powyższym wzorze dodaliśmy index $12$ aby podkreślić że ten kąt jest między włóknami $1$ i $2$. Identyczne kalkulacje możemy przeprowadzić dla pozostałych kombinacji wektorów bazowych. Zależność tą możemy przekształcić do następującej postaci
$$C_{12} = \sin(\gamma_{12}) \lambda_1 \lambda_2$$ $$C_{13} = \sin(\gamma_{13}) \lambda_1 \lambda_3$$ $$C_{23} = \sin(\gamma_{23}) \lambda_2 \lambda_3$$Składowe styczne tensora deformacji $\C$ są równe sinusowi kąta odkształcenia postaciowego między włóknami materialnym pomnożonymi przez względne rozciągnięcie tych włókien.
Jeżeli kąt pomiędzy włóknami nie zmienił się podczas deformacji, to $\sin(\gamma)=0$.
Tensor odkształcenia Greena
Zdefiniujmy przyrost długości włókna materialnego jako
$$\lambda = \cfrac{dl}{dL}, \qquad dl = dL + du = (dL + du)/dL \cdot dL = \left(\cfrac{dL}{dL} + \cfrac{du}{dL}\right)dL = (1+\varepsilon)dL \rightarrow \lambda =\varepsilon+1$$• składowe normalne
$$\varepsilon^G_{11} = \cfrac{1}{2}(C_{11}-1) = \cfrac{1}{2}(\lambda_1^{2}-1) =\cfrac{1}{2}(\varepsilon_1^{2}+2\varepsilon_1)\approx \varepsilon_1$$ $$\varepsilon^G_{22} = \cfrac{1}{2}(C_{22}-1) = \cfrac{1}{2}(\lambda_2^{2}-1) =\cfrac{1}{2}(\varepsilon_2^{2}+2\varepsilon_2)\approx \varepsilon_2$$ $$\varepsilon^G_{33} = \cfrac{1}{2}(C_{33}-1) = \cfrac{1}{2}(\lambda_3^{2}-1) =\cfrac{1}{2}(\varepsilon_3^{2}+2\varepsilon_3)\approx \varepsilon_3$$• składowe styczne
Wykorzystując przybliżenie dla małych katów $\sin(\alpha) = \alpha$. Obydwa względne rozciągnięcia możemy przyjąć równe
$$\varepsilon^G_{12} = \cfrac{1}{2}C_{12} = \cfrac{1}{2}\sin(\gamma_{12}) \lambda_1 \lambda_2 = \cfrac{1}{2}\gamma_{12}(1+\varepsilon_1)(1+\varepsilon_2) = \cfrac{1}{2}\gamma_{12}(1 +\varepsilon_1+\varepsilon_2+\varepsilon_1\varepsilon_2) \approx \cfrac{1}{2}\gamma_{12}$$ $$\varepsilon^G_{13} = \cfrac{1}{2}\gamma_{13}$$ $$\varepsilon^G_{23} = \cfrac{1}{2}\gamma_{23}$$W powyższych wzorach pominęliśmy wszystkie nieliniowe człony $\gamma\varepsilon$.
Linearyzacja tensora Greena prowadzi do odkształceń poza przekątną główną równych połowie wartości kąta odkształcenia postaciowego.