Wektory i macierze

Wektory i macierze będziemy zapisywać używając trzech różnych konwencji. Wektor o trzech składowych zapiszemy używając pogrubionego symbolu, zwykłego symbolu z indeksem dolnym oraz stosując nawiasy kwadratowe

$$\a, a_i, \quad [1, 5, 2]$$

W analogiczny sposób będziemy zapisywać macierz stosując dwa indeksy dolne oraz układ wierszy i kolumn. Kolumny numerujemy od lewej do prawej natomiast wiersze od góry do dołu.

$$\A, A_{ij}, \quad \matt{2}{3}{1}{4}$$

Liczbę elementów wektora (jego wymiar) określa zakres wskaźników. Jeżeli nie podano inaczej to występujące wskaźniki dolne będą miały zakresy równe od 1 do 3.

Macierz jednostkową (deltę Kroneckera) oznaczać będziemy następującymi symbolami

$$\I, \delta_{ij}, \quad \mat{1}{0}{0}{0}{1}{0}{0}{0}{1}$$

Operacje na wektorach i macierzach

Możemy dodawać i odejmować wektory i macierze tylko o takich samych wymiarach

Mnożenie wektora lub macierzy przez skalar oznacza pomnożenie przez tą wartość wszystkich składowych danego wektora lub macierzy

$$2 \cdot \vr{2}{3}{4} = \vr{4}{6}{8}$$

Transpozycja macierzy (tylko macierz kwadratowa czyli taka dla której liczba wierszy jest równa liczbie kolumn) polega na zamianie wskaźników

$$A_{ij}^T = A_{ji}$$ $$\mat{1}{2}{3}{4}{5}{6}{7}{8}{9}^T = \mat{1}{4}{7}{2}{5}{8}{3}{6}{9}$$

Mnożenie dwóch macierzy (konwencja sumacyjna)

$$\C = \A \cdot \B$$ $$C_{ij} = \sum_{k=1}^{3}A_{ik}B_{kj} = A_{ik}B_{kj}$$

Mnożenie macierzy i wektora

$$\w = \A \cdot \v$$ $$w_{i} = \sum_{j=1}^{3}A_{ij}v_{j} = A_{ij}v_{j}$$

Przykładowe zagadnienia teorii sprężystości

Zagadnienie Boussinesqa

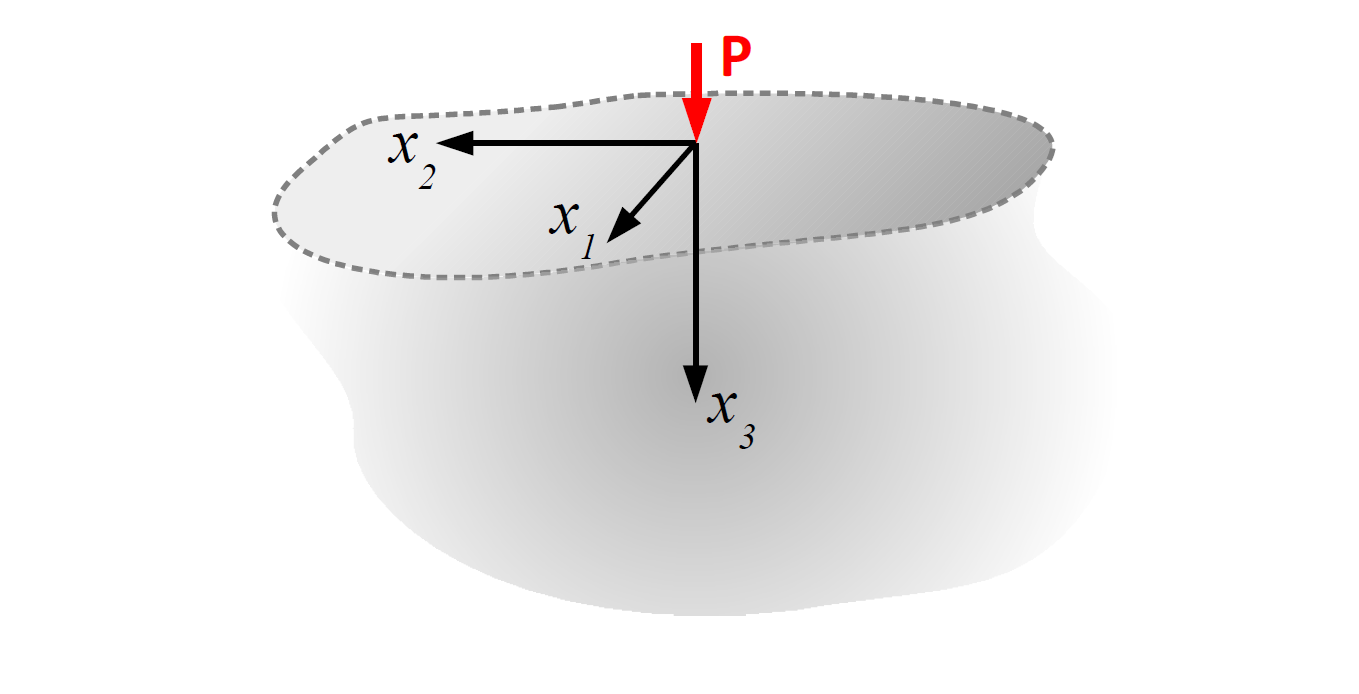
Zagadnienie Boussinesqa dotyczy liniowej teorii sprężystości i polega na wyznaczeniu naprężeń, odkształceń oraz przemieszczeń w jednorodnej, izotropowej półprzestrzeni sprężystej (materiał Hooke'a) obciążonej siłą skupioną, przyłożoną na płaszczyźnie ograniczającej półprzestrzeń, prostopadłą do niej. Siła ma wartość $P$, a materiał charakteryzują stałe sprężyste $\lambda$ i $G$. Zakłada się brak przemieszczeń i obrotów półprzestrzeni oraz minimalny wpływ siły w odległych punktach. Siła działa w początku układu współrzędnych wzdłuż osi $x_3$,

Równanie rządzące zagadnieniem

$$G u_{i,jj} + (G+\lambda)u_{j,ji} + b_i = \rho \ddot{u}_i, \quad i=1,2,3, \quad j=1,2,3$$

Warunki brzegowe na przemieszczenia i ich pochodne

$$\lim_{R\rightarrow \infty} u_i = 0, \quad \lim_{R\rightarrow \infty} u_{i,j} = 0,$$

Warunki dla płaszczyzny $x_3=0$ i $x_1 \neq 0, \quad x_2 \neq 0$

$$\sigma_{13}=\sigma_{23}=\sigma_{33}0, \quad$$

Uwzględnienie siły skupionej (dla $x_1=x_2=x_3 = 0$)

$$\sigma_{33} = -P\delta_0, \quad \sigma_{13}=\sigma_{23}=0$$

Dla powyższego zagadnienie parametry $G$ i $\lambda$ to stałe materiałowe. Zakładamy że $b_i=0$ (brak wpływu sił masowych oraz $\ddot{u}_i=0$ (statyka).

Rozwiązanie (pole przemieszczenia)

$$u_{1}=\cfrac{P\,x_{1}}{4\pi\,G}\biggl[\cfrac{x_{3}}{R^{3}}-\cfrac{1-2\,\nu}{R(R+x_{3})}\biggr]$$ $$u_{2}=\cfrac{P x_{2}}{4\pi \,G}\biggl[\cfrac{x_{3}}{R^{3}}-\cfrac{1-2\,\nu}{R(R+x_{3})}\biggr]$$ $$u_{3}=\cfrac{P}{4\pi G}\biggl[{\frac{x_{3}^{2}}{R^{3}}}+(3-4\nu){\frac{1}{R}}-{\frac{1-2\,\nu}{R+x_{3}}}\biggl({\frac{x_{3}}{R}}+1\biggr)\biggr]$$ $$\nu = \cfrac{\lambda}{2(\lambda + G)}$$