Wprowadzenie
Teoria konstrukcji inżynierskich zajmuje się analizą i projektowaniem konstrukcji, które ulegają deformacjom pod wpływem obciążeń. Problemy te są opisywane za pomocą równań różniczkowych cząstkowych. Znajomość tych równań jest niezbędna do skutecznego modelowania i analizy zjawisk w konstrukcjach.
Rzeczywista konstrukcja Rozpoczynamy od rzeczywistego obiektu lub struktury, którą chcemy zrozumieć. To może być most, budynek, maszyna lub inny element.
Model fizyczny - idealizacja : Następnie tworzymy uproszczony model fizyczny, który reprezentuje naszą konstrukcję. W tym kroku wybieramy, które aspekty uwzględnić, a które zignorować. Na przykład możemy zastąpić skomplikowane kształty prostymi bryłami geometrycznymi.
Model matematyczny - równania różniczkowe W ostatnim kroku przekształcamy nasz model fizyczny w zestaw równań różniczkowych. Te równania opisują zachowanie konstrukcji pod wpływem obciążeń, naprężeń i deformacji. Rozwiązując te równania, możemy uzyskać informacje na temat wygięć, naprężeń i innych właściwości konstrukcji.
Model numeryczny - np. Metoda Elementów Skończonych, Używamy jej aby rozwiązać w sposób przybliżony równania różniczkowe.

Powtórka wiadomości z algebry i analizy matematycznej
Funkcja jednej i wielu zmiennych
Funkcja jednej zmiennej $f(x)$ jest to przyporządkowanie każdemu elementowi $x$ z pewnego zbioru (zwanego dziedziną funkcji) dokładnie jednego elementu $y=f(x)$ z innego zbioru (zwanego przeciwdziedziną funkcji).
Matematycznie można to zapisać jako
$$f: \mathbb{R} \rightarrow \mathbb{R}$$Funkcja, która przyjmuje wiele argumentów i zwraca wiele wartości, nazywana jest funkcją wektorową wielu zmiennych. Formalnie, taka funkcja jest przyporządkowaniem
$$f: \mathbb{R}^n \rightarrow \mathbb{R}^m,$$gdzie $ n $ oznacza liczbę argumentów (zmiennych wejściowych), a $m $ oznacza liczbę wartości wyjściowych (składowych wektora wartości). Każdemu wektorowi argumentów $(x_1, x_2, \ldots, x_n) $ z przestrzeni $\mathbb{R}^n $ przyporządkowany jest wektor wartości \( (y_1, y_2, \ldots, y_m) \) z przestrzeni $ \mathbb{R}^m $
Przykładem może być funkcja
$$f(x, y) = (x + y, x^2 - y^2, \sin(xy))$$która dla pary argumentów $(x, y)$ zwraca trójkę wartości $ (x + y, x^2 - y^2, \sin(xy) ) $.
# Przykład
Wizualizacja funkcji wielu zmiennych
$$T(x,y,z) = \cfrac{1}{1000}\left((x+100)^2 + (y-20)^2 + 2z\right) +1$$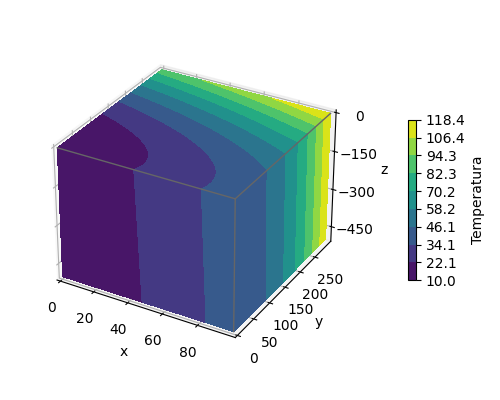
Pochodna zwyczajna, pochodna cząstkowa
Pochodna zwyczajna odnosi się do zmiany funkcji jednej zmiennej względem tej zmiennej, mierząc szybkość zmiany funkcji wzdłuż jednej osi, np. $ f'(x) $ lub $\frac{dy}{dx} $. Pochodna cząstkowa natomiast dotyczy funkcji wielu zmiennych i mierzy szybkość zmiany funkcji względem jednej z tych zmiennych, przy założeniu, że pozostałe zmienne są stałe. Jest zapisywana jako $ \frac{\partial f}{\partial x} $ lub $ \frac{\partial f}{\partial y} $.
# Przykład
Znajdź wszystkie pochodne pierwszego rzędu dla następującej funkcji wielu zmiennych
$$f(x,y,z) = x^2 + xy+ z+ 2 +x^2z^2$$Rozwiązanie
$$\pp{f}{x} = 2x + y + 2z^2x, \quad \pp{f}{y} = x, \quad \pp{f}{z} = 1 + 2x^2z$$Przykładowy skrypt języka PYTHON do wyznaczania pochodnych funkcji
from sympy.abc import x, y,z
from sympy import diff
f = x**2 + x*y + z +2 +x**2*z**2
rx = diff(f, x)
ry = diff(f, y)
rz = diff(f, z)
print(rx)
print(ry)
print(rz)
Równania różniczkowe zwyczajne
Równania różniczkowe zwyczajne to takie równania w których występuję tylko jedna zmienna niezależna $x$. Są to równania które można w ogólne postaci zapisać jako:
$$F\left(x,u, \cfrac{du}{dt}, \cfrac{d^2u}{dx^2}, ..., \cfrac{d^ku}{dx^k}\right) = F\left(x,u, u{'}, u{''}, ..., u^{k\times}{'}\right) = F(u)=0,$$gdzie $u' = \dd{u}{x}$, $\quad u'' = \dd{^2u}{x^2}$ itd.
Takie równanie różniczkowe zwyczajne nazywamy równaniem różniczkowym rzędu $k$. O rzędzie danego równania różniczkowego decyduje najwyższy rząd pochodnej występujący w równaniu.
Przykłady równań różniczkowych
$$\dd{u(x)}{x} = 2$$ $$2u'' + 3u' - u = x$$ $$(u'')^2 + \sin (x)u''' - u^2 = 0$$Rozwiązaniem równania różniczkowego jest rodzina funkcji $u(x)$ spełniająca dane równanie różniczkowe.
# Przykład
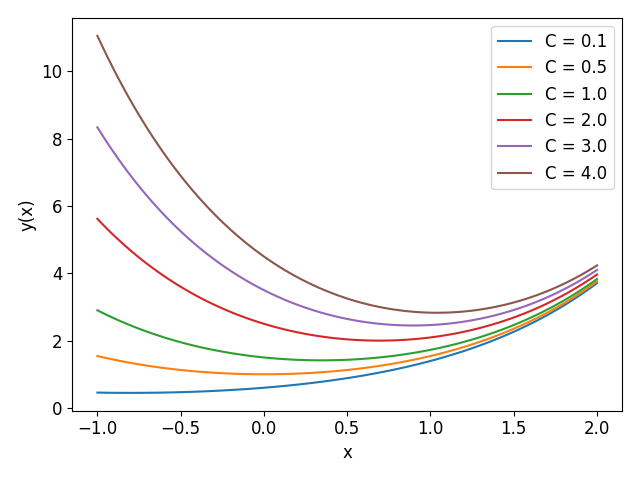
Znajdź postać funkcji $y(x)$ która spełnia następujące równanie różniczkowe
$$y'(x) + y(x) = e^x$$Rozwiązaniem ogólnym powyższego równania (stosując metodę czynnika całkującego) jest funkcja
$$y(x) = \cfrac12 e^x + C e^{-x}$$
gdzie $C$ jest stałą całkowania. Podstawiając różne wartości stałej $C$ dostajemy rodzinę funkcji spełniających zadane równanie różniczkowe
Przykładowy skrypt języka PYTHON do rozwiązywania równań różniczkowych
from sympy import Function, dsolve, Derivative, exp
from sympy.abc import x
y = Function('y')
result = dsolve(Derivative(y(x), x) + y(x)-exp(x))
print(result)
Równania różniczkowe cząstkowe
Równania różniczkowe cząstkowe to równania w których pochodne występujące w równaniu różniczkowym są obliczane względem wielu zmiennych.
$$F\left(x_i, \cfrac{\partial u}{\partial x_i}, \cfrac{d^2u}{dx_i^2}, ..., \cfrac{\partial^ku}{\partial x_i^k}, \cfrac{\partial^2u}{\partial x_i \partial x_j}, \cfrac{\partial^3u}{\partial x_i \partial x_j \partial x_k} \right)=0, \quad i=1,2,..., n$$Przykłady równań różniczkowych cząstkowych
• równanie falowe
$$\pp{^2 u}{t^2} - c^2\left(\pp{^2 u}{x_1^2} + \pp{^2 u}{x_2^2} +\pp{^2 u}{x_3^2}\right) = f,$$Poszukiwaną funkcją jest funkcja $u(x_1, x_2, x_3, t)$ opisująca wychylanie fali w czasie i przestrzeni.
• płyty cienkie Kirchhoffa-Love'a - stan giętny
$$\pp{^4 w(x_1,x_2)}{x_1^4} + 2\pp{^4 w(x_1,x_2)}{x_1^2 \partial x_2^2} + \pp{^4 w(x_1,x_2)}{x_2^4} = \cfrac{q}{D}$$Poszukiwaną funkcją jest funkcja ugięcia płyty $w(x_1, x_2)$.
• równanie przewodnictwa cieplnego
$$\dd{T}{t} = a \left( \pp{^2T}{x_1^2} + \pp{^2T}{x_2^2} + \pp{^2T}{x_3^2} \right)$$Poszukiwaną funkcją jest funkcja temperatury $T(x, y, z, t)$.
# Przykład
Znajdź postać funkcji $u(x,t)$ która spełnia następujące równanie różniczkowe cząstkowe
$$\pp{u}{t} + c\pp{u}{x} = 0$$Rozwiązanie
$$u(x,t) = f(x-ct)$$gdzie $f$ to dowolna funkcja określona na podstawie warunku początkowego. Dla przykładu przyjmijmy że $f = sin$. Dostajemy wtedy
$$u(x,t) = \sin(x-ct)$$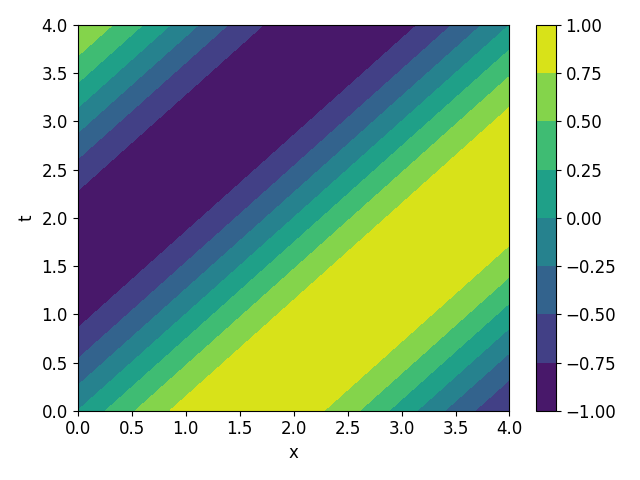
Zagadnienie brzegowe
Zagadnienie brzegowe – problem polegający na znalezieniu funkcji spełniającej dane równanie różniczkowe zdefiniowane w rozważanym obszarze wraz z warunkami brzegowymi które nałożone są na wartości funkcji i jej pochodne w więcej niż jednym punkcie tego obszaru.
Rozważamy dwa typy warunków brzegowych:
• warunek brzegowy Dirichleta (podstawowy) zadany na poszukiwaną funkcję
• warunek brzegowy Neumanna (naturalny) zadany na pochodną poszukiwanej funkcji
# Przykład
Znajdź postać funkcji $y(x)$ która spełnia następujące równanie różniczkowe zwyczajne
$$y'(x) + y(x) = e^x$$wraz z warunkiem brzegowym Dirichleta $y(0)=1$
Podstawiamy $x=0$ oraz $y=1$ do rozwiązania ogólnego z poprzedniego przykładu
$$1 = \cfrac12 e^0 + C e^0 \Rightarrow C= \cfrac12$$from sympy import Function, dsolve, Derivative, exp
from sympy.abc import x
y = Function('y')
# y'(x) + y(x) = e^x
# y(0) = 1
r = dsolve(Derivative(y(x), x) + y(x)-exp(x), ics={y(0): 1})
print(r)
Notacja przecinkowa
Notacja przecinkowa w zapisie pochodnych cząstkowych jest używana jako alternatywa dla klasycznego oznaczenia z operatorem $\partial$. W tej notacji pochodną cząstkową funkcji względem danej zmiennej oznacza się przecinkiem, po którym następuje indeks oznaczający zmienną. Na przykład, pochodna cząstkowa funkcji $u(x, y)$ względem $x$ może być zapisana jako $u_{,x}$, a druga pochodna względem $x$ jako $u_{,xx}$.
Przykład: dla równania falowego, klasyczny zapis
$$\cfrac{\partial^2 u}{\partial t^2} = c^2 \cfrac{\partial^2 u}{\partial x^2}$$może być zapisany w notacji przecinkowej jako:
$$u_{,tt} = c^2 u_{,xx}.$$W większości przypadków będziemy używać cyfr do oznaczania różniczkowania względem zmiennych $x$, $y$ i $z$ według zależności
$$x\rightarrow x_1, \quad y \rightarrow x_2, \quad z \rightarrow x_3,$$czyli następujące pochodne funkcji $u(x,y,z)=u(x_1, x_2, x_3)$ możemy zapisać jako
$$u_{1,2} = u_{x,y} = \pp{u_1}{x_2} = \pp{u_x}{y}$$ $$u_{2,23} = u_{y,yz} = \pp{^2u_2}{x_2\partial x_3} = \pp{^2u_y}{y \partial z}$$