Płaski stan naprężenia i odkształcenia
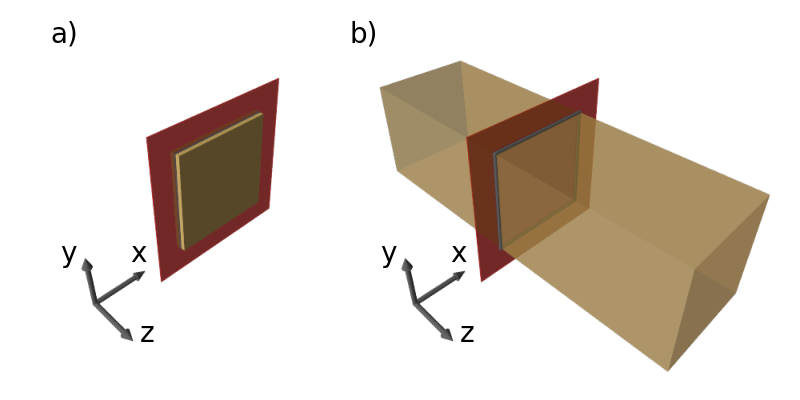
Tarczą nazywamy bryłę o jednym wymiarze (grubość) dużo mniejszym od pozostałych. W tarczy panuje płaski stan naprężenia (PSN).
Dyskretyzacja
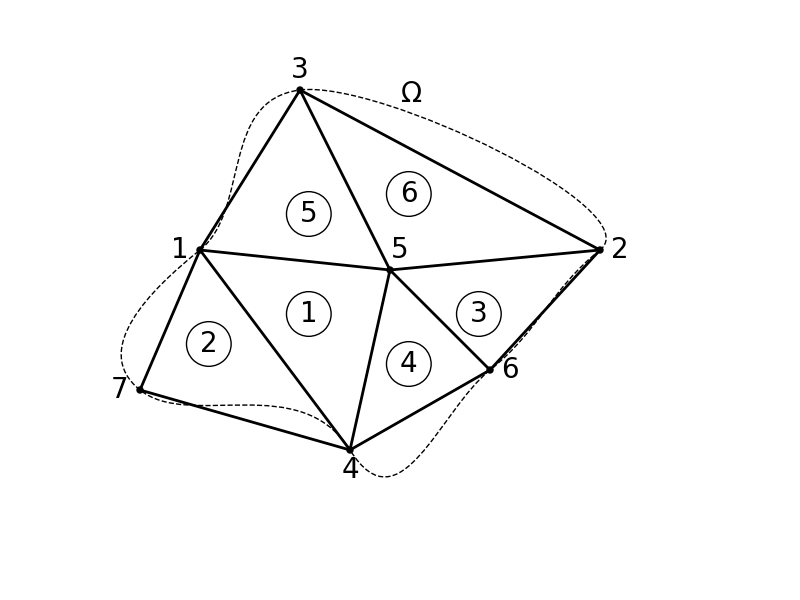
Dwuwymiarowy obszar dzielimy na skończoną liczbę elementów w postaci figur płaskich. Najczęściej stosowanymi elementami wykorzystywanymi do zagadnień dwuwymiarowych są elementy trójkątne i czworokątne.
Wektor przemieszczenia ma tylko dwie składowe
$$\u = [u_x, u_y]^T$$Wektor odkształcenia i naprężenia jest następujący
$$\boldsymbol{\varepsilon} = [\varepsilon_{xx}, \varepsilon_{yy}, \gamma_{xy}] \quad \boldsymbol{\sigma} = [\sigma_{xx}, \sigma_{yy}, \sigma_{xy}]$$Dla PSN zakładamy że składowa $zz$ tensora naprężenia jest równa zero. Podobnie w przypadku PS0 tensor odkształcenia ma zerową składową na kierunku $zz$. Związek między wektorem naprężenia i odkształcenia możemy wyrazić przez macierz zawierającą stałe sprężyste, która dla liniowego prawo Hooke'a jest następująca
Macierz sztywności elementu skończonego możemy zapisać jako całkę po powierzchni wykorzystując założenie, że na elemencie skończonym jego grubość nie ulega zmianie.
$$\boldsymbol{k} = h \int_{A} (\B)^T \D \B dxdy$$gdzie $A, h$ - oznacza powierzchnię i grubość elementu skończonego.
Trójwęzłowy element o stałym odkształceniu
Do aproksymacji pola przemieszczenia wystarczająca jest liniowa interpolacja Lagrange’a
$$\u = \N\d, \quad u = \sum_{i=1}^3 N_i(x,y) u_i, \quad v = \sum_{i=1}^3 N_i(x,y) v_i$$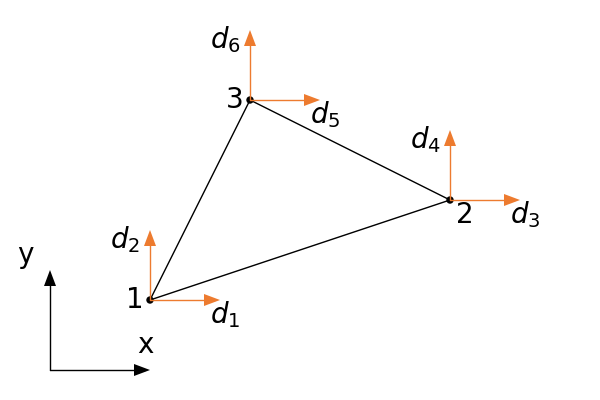
Wektor przemieszczeń węzłowych ma postać
$$\boldsymbol{d} = [u_1, v_1, u_2, v_2, u_3, v_3]^T$$Funkcje kształtu zawarte są w macierzy $\N$
$$\N^e = \begin{bmatrix} N_1 & 0 & N_2 & 0 & N_3 & 0\\ 0 & N_1 & 0 & N_2 & 0 & N_3\\ \end{bmatrix}$$Zakładamy że funkcję opisujące pole przemieszczenia są liniowo zależne od $x$ i $y$ czyli
$$u = c_1 + c_2 x + c_3 y, \quad v = c_4+ c_5x + c_6 y$$Liniowe funkcje kształtu mają następującą postać
gdzie $A$ - to pole powierzchni elementu skończonego a $x_i$ oraz $y_i$ to współrzędne węzłów dla $i=1,2,3$.

Odkształcenie w elemencie skończonym obliczamy wykorzystując macierz $\mathbf{L}$. Dla przypadku dwuwymiarowego ma ona postać
Odkształcenie jest więc równe
$$\ee = \B \boldsymbol{d}$$Widać, że odkształcenie na elemencie jest stałe. Macierz $\B$ nie zależy od $x$ i $y$. ang. Constant strain triangle element (CST element).
Sześciowęzłowy element trójkątny o liniowej aproksymacji pola odkształcenia
Kolejnym elementem służącym do analizy płaskiego stanu naprężenia oraz odkształcenia jest sześciowęzłowy element trójkątny zwany w literaturze skrótowo LST (Linear Strain Triangle). Każdy z węzłów ma, podobnie jak w elemencie CST, po dwa stopnie swobody. Wektor przemieszczeń węzłowych definiujemy w następujący sposób
$$\boldsymbol{d} = [u_1, u_2, u_3, u_4, u_5, u_6, v_1, v_2, v_3, v_4, v_5, v_6].$$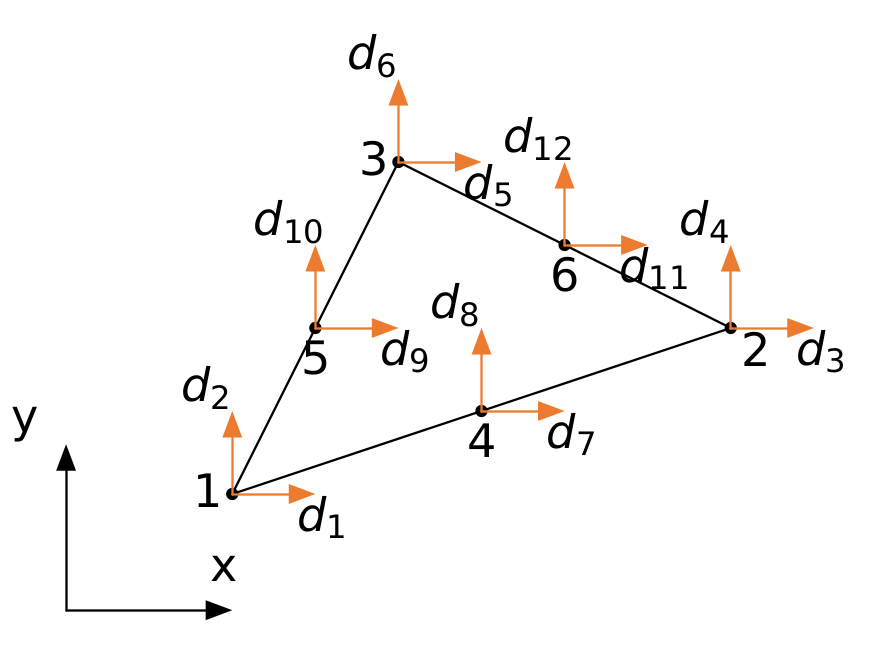
Funkcja opisujące poszczególne składowe pole przemieszczenia jest następująca
$$u = c_1 + c_2x+c_3y + c_4x^2+c_5xy+c_6 y^2$$ $$v = c_7 + c_8x+c_9y + c_{10}x^2+c_{11}xy+c_{12} y^2$$