Element ramowy 2d

Rozważmy płaską ramę, którą dzielimy na elementy skończone.

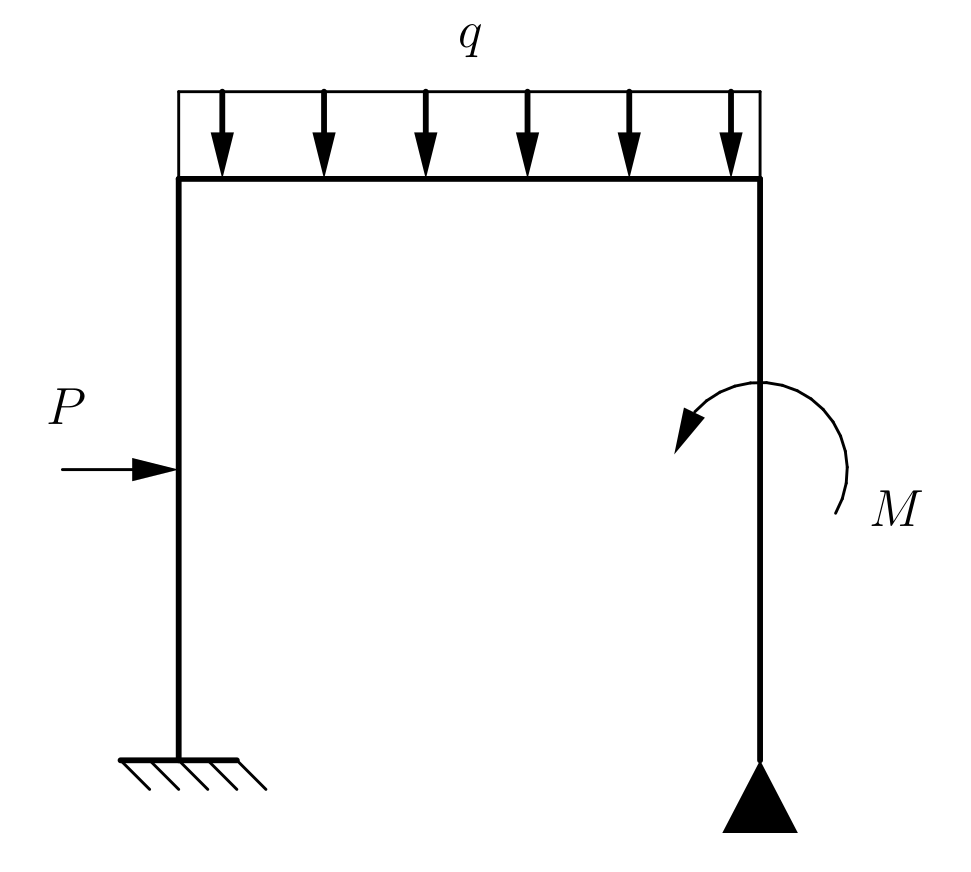
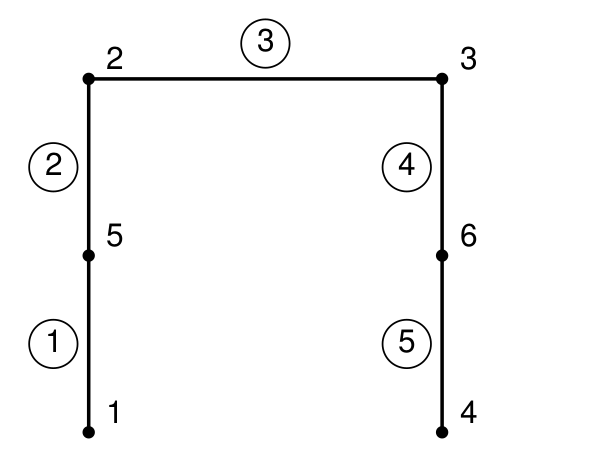
Dyskretyzacja rama

O gęstości i charakterze podziału decydują kształt, obciążenie oraz własności materiału.

Równania opisujące element skończony ramy

Element skończony dla ramy jest złożeniem elementu prętowego o sztywności $EA$ i obciążeniu ciągłym $q^p$ i elementu belkowego o sztywności $EI$ i obciążeniu ciągłym $q^b$ . W każdym węźle mamy po trzy uogólnione przemieszczenia węzłowe i odpowiadające im uogólnione siły węzłowe. Uogólnione przemieszczenia i siły węzłowe dla elementu skończonego ramy mogą być przedstawione w układzie lokalnym i globalnym.

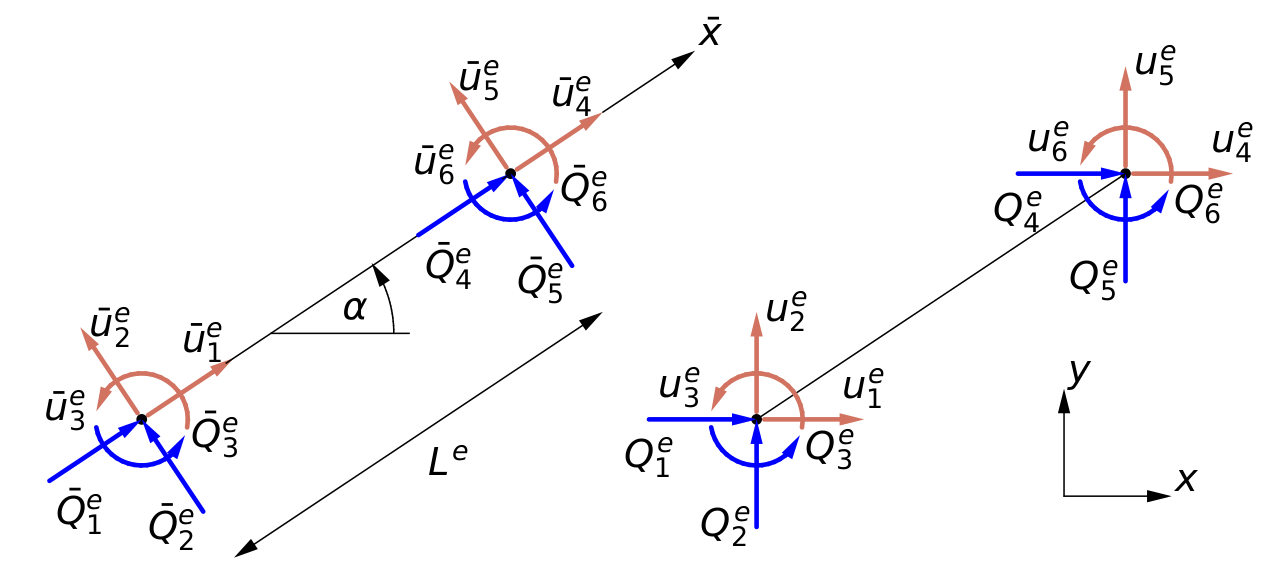
Przypomnijmy macierz sztywności dla pręta, oraz macierz sztywności dla belki. Wprowadźmy dodatkowe indeksy dolne do oznaczenia tych macierzy. Indeks dolny $_p$ odnosi się do pręta, natomiast indeks $_b$ oznacza belkę.

$$\boldsymbol{k}_p = \cfrac{EA}{L} \matt{1}{-1}{-1}{-1} \qquad \boldsymbol{k}_b = \cfrac{2EI}{L^3} \begin{bmatrix} 6 & 3L & -6 & 3L\\ 3L & 2L^2 & -3L^e & L^2\\ -6 & -3L & 6 & -3L\\ 3L & L^2 & -3L & 2L^2\\ \end{bmatrix}$$

Po połączeniu obu macierzy dostajemy lokalną postać macierzy sztywności dla elementu ramy

$$\bar{\boldsymbol{k}}= \cfrac{EA}{L} \begin{bmatrix} 1 & 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ \end{bmatrix} + \cfrac{2EI}{L^3} \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 6 & 3L & 0 & -6 & 3L\\ 0 & 3L^e & 2L^2 & 0 & -3L & L^2\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & -6 & -3L & 0 & 6 & -3L\\ 0 & 3L & L^2 & 0 & -3L & 2L^2\\ \end{bmatrix}$$

W analogiczny sposób wyznaczamy lokalny wektor obciążeń zewnętrznych jako sumę obciążeń pręta i belki. Wektory obciążeń ciągłych odpowiednio dla pręta i belki są następujące

$$\f_p = \cfrac{1}{2}q^pL\vcc{1}{1},\quad \f^b = \cfrac{q^bL}{12}\begin{bmatrix} 6\\ L\\ 6\\ -L\\ \end{bmatrix}$$

aby je do siebie dodać musimy zapisać je używając wspólnego układu współrzędnych. Dodatkowo musimy zmienić nazwy obciążeń ciągłych

$$\bar{\f} = \cfrac{q^PL}{2}\begin{bmatrix} 1\\0\\0\\1\\0\\0\\ \end{bmatrix} + \cfrac{q^BL}{12}\begin{bmatrix} 0\\6\\L\\0\\6\\-L\\ \end{bmatrix}$$

Analogicznie postępujemy z wektorem obciążeń węzłowych. Układ równań dla elementu ramy w układzie lokalnym możemy więc zapisać jako

$$\bar{\boldsymbol{k}}\bar{\u} = \bar{\f} + \bar{\Q}$$

Aby otrzymać powyższe równanie w układzie globalnym musimy dokonać transformacji

$$\T = \begin{bmatrix} \t & \mathbf{0} & \mathbf{0} &\mathbf{0} \\ \mathbf{0} & 1 & \mathbf{0} & 0 \\ \mathbf{0} & \mathbf{0} & \mathbf{t} & \mathbf{0}\\ \mathbf{0} & 0 & \mathbf{0} &1\\ \end{bmatrix} \quad \mathbf{t} = \matt{\cos\alpha}{\sin\alpha}{-\sin\alpha}{\cos \alpha}$$

Kąt $\alpha$ jest kątem transformacji o dodatnim znaku. Stosując prawo transformacji dostajemy macierze sztywności jako

$$\boldsymbol{k} = \T^T \bar{\boldsymbol{k}}\T$$

Podobnie dla wektora sił węzłowych i przemieszeń węzłowych i wektora obciążeń ciągłych

$$\f = \T^T \bar{\f}, \quad \Q = \T^T \bar{\Q}, \quad \u = \T^T \bar{\u}$$

Wykonując powyższe operacje dostajemy równanie

$$\boldsymbol{k} \u =\f + \Q$$