Element belkowy

Dana jest belka wspornikowa wykonana z materiału o sztywności $E$ i przekroju poprzecznym którego moment bezwładności jest równy $I$. Belka obciążona jest obciążeniem ciągłym $q(x)$. Belka jest utwierdzona na początku.

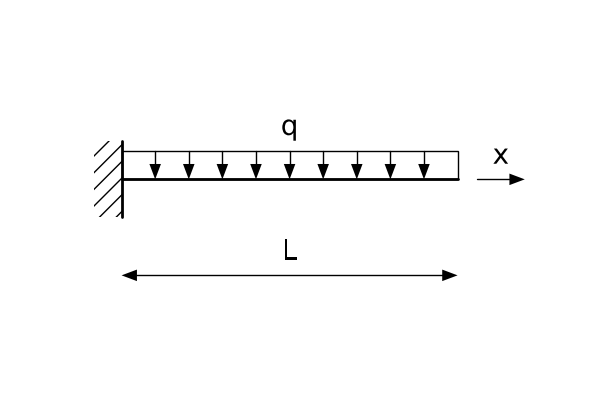
Równanie różniczkowe opisujące ugięcie osi belki jest następujące

$$EI\cfrac{d^4 u(x)}{dx^4} = q(x)$$

Powyższe równanie jest równaniem różniczkowym czwartego rzędu więc należy uzupełnić go o cztery warunki brzegowe
• ugięcie $u(x)$
• kąt obrotu $\cfrac{du}{dx}$
• moment zginający $EI \cfrac{d^2u}{dx^2}$
• siła poprzeczna $EI \cfrac{d^3u}{dx^3}$

Dyskretyzacja belki

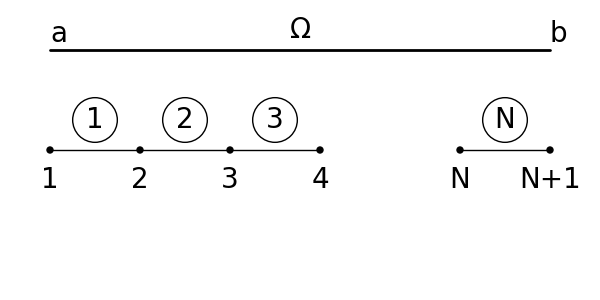
O gęstości i charakterze podziału decydują kształt, obciążenie oraz własności materiału.

Równania opisujące element skończony belki

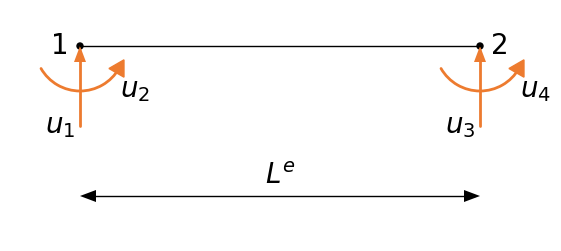
Przybliżonego rozwiązania na danym elemencie poszukujemy dla następującego wielomianu

$$u(x) \approx \sum_{i=1}^{4} u_iN_i$$

gdzie $u_i$ są nieznanymi parametrami (przemieszczenia i kąty obrotu danego węzła)Funkcje kształtu dobieramy jako:

$$N_1(x) = 1 - 3\left(\cfrac{x-x_1}{x_2-x_1}\right)^2 + 2\left(\cfrac{x-x_1}{x_2-x_1}\right)^3 \quad N_2(x) = (x-x_1)\left(1-\cfrac{x-x_1}{x_2-x_1}\right)^2$$ $$N_3(x) = 3\left(\cfrac{x-x_1}{x_2-x_1}\right)^2 -2\left(\cfrac{x-x_1}{x_2-x_1}\right)^3 \quad N_4(x) = (x-x_1)\left[\left(\cfrac{x-x_1}{x_2-x_1}\right)^2 - \cfrac{x-x_1}{x_2-x_1}\right]$$

Są to wielomiany Hermite'a. Funkcje te mają taką własność, że ich wartości oraz pierwsze pochodne na końcach przedziału są równe 0 lub 1. Dla przykładu funkcja $N_1(x)$

$$N_1(x_1) = 1, \quad N_1(x_2) = 0, \quad \cfrac{dN_1(x_1)}{dx} = 0, \quad \cfrac{dN_1(x_2)}{dx} = 0$$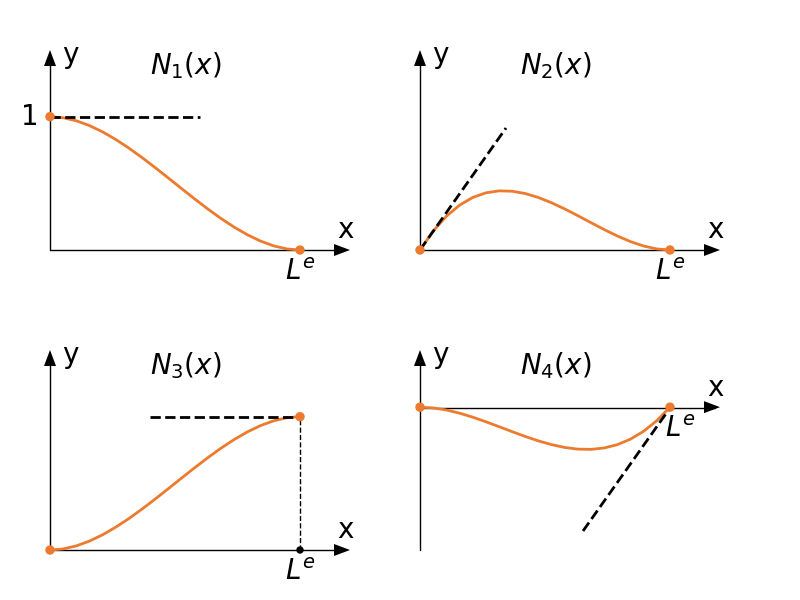

Zapiszmy jak wcześniej nasze przybliżone rozwiązanie na elemencie stosując zapis macierzowy

$$u = \N\u, \quad \N = \begin{bmatrix} N_1 & N_2 & N_3 & N_4 \end{bmatrix}, \quad \u = \begin{bmatrix} u_1 & u_2 & u_3 & u_4 \end{bmatrix}^T$$

Wstawmy nasze przybliżone rozwiązanie do równania różniczkowego

$$R = EI\cfrac{d^4 \N\u}{dx^4} - q(x) \neq 0, \quad x \in \Omega$$

Pomnóżmy reziduum przez wagę równą funkcji $u$ i scałkujmy po elemencie skończonym. Przyrównajmy to wszystko do zero (metoda ważonych reziduów)

$$EI \int_{x_1}^{x_2} \N^T \cfrac{d^4 \N\u}{dx^4} dx - \int_{x_1}^{x_2} \N^T q dx = 0$$

Wykonajmy całkowanie przez części dla pierwszej całki dwukrotne $\int f(x) \cdot g{'}(x) dx = f(x) \cdot g(x) - \int f{'}(x) \cdot g(x) dx$

$$EI \int_{x_1}^{x_2} \N^T \cfrac{d^4 \N\u}{dx^4} dx = -EI \int_{x_1}^{x_2} \cfrac{d\N^T}{dx} \cfrac{d^3 \N}{dx^3}dx \u+ EI \N^T \cfrac{d^3 \N}{dx^3}\u|_{x_1}^{x_2} =$$ $$EI \int_{x_1}^{x_2} \cfrac{d^2\N^T}{dx^2} \cfrac{d^2\N}{dx^2}dx \u + EI \N^T\cfrac{d^3 \N}{dx^3}\u|_{x_1}^{x_2} - EI \cfrac{d\N^T}{dx} \cfrac{d^2 \N}{dx^2}\u|_{x_1}^{x_2}$$

Wprowadźmy następujące oznaczenia

$$Q_1^e = EI\cfrac{d^3 \N}{dx^3}\u|_{x_1}, \quad Q_2 = -EI\cfrac{d^2 \N}{dx^2}\u|_{x_1}, \quad Q_3 = -EI\cfrac{d^3 \N}{dx^3}\u|_{x_2}, \quad Q_4 = EI\cfrac{d^2 \N}{dx^2}\u|_{x_2}$$

Po uwzględnieniu oznaczeń dostajemy

$$EI \int_{x_1}^{x_2} \cfrac{d^2 \N^T}{dx^2} \cfrac{d^2\N}{dx^2}dx \u -\int_{x_1}^{x_2} \N^T q dx -\N^T Q_1 - \cfrac{d\N^T}{dx} Q_2 -\N^T Q_3 - \cfrac{d\N^T}{dx}Q_4 =0$$

Wprowadzmy kolejne oznaczenia

$$\boldsymbol{k} = EI \int_{x_1}^{x_2} \cfrac{d^2 \N^T}{dx^2} \cfrac{d^2\N}{dx^2}dx, \quad \f = \int_{x_1}^{x_2} \N^T q dx, \quad \Q = \N^T Q_1 + \cfrac{d\N^T}{dx} Q_2 + \N^T Q_3 + \cfrac{d\N^T}{dx} Q_4$$

Stosując powyższe oznaczenie nasze równania możemy zapisać jako

$$\boldsymbol{k} _{4\times 4} \u_{4\times 1} = \f_{4\times 1} + \Q_{4\times 1}$$

Policzmy pierwszy element macierzy sztywności

$$k_{11} = EI \int_{x_1}^{x_2}\cfrac{d^2 N_1}{dx^2} \cfrac{d^2N_1}{dx^2}dx= \cfrac{12EI}{L^3}$$

Wykonując powyższe operacje dla wszystkich kombinacji funkcji kształtu dostajemy

$$\boldsymbol{k} = \cfrac{2EI}{L^3} \begin{bmatrix} 6 & 3L & -6 & 3L\\ 3L & 2L^2 & -3L & L^2\\ -6 & -3L & 6 & -3L\\ 3L & L^2 & -3L & 2L^2\\ \end{bmatrix} \quad \f = \cfrac{qL}{12}\begin{bmatrix} 6\\ L\\ 6\\ -L\\ \end{bmatrix} \quad \Q = \begin{bmatrix} Q_1\\ Q_2\\ Q_3\\ Q_4\\ \end{bmatrix}$$

Agregacja elementów skończonych

Połączenie w jedną całość elementów skończonych tworzących belkę wymaga uwzględnienia w każdym wspólnym węźle. Rozpatrzmy więc dwa sąsiadujące ze sobą elementy skończone $e$ i $e+1$
• warunków ciągłości: ciągłość ugięcia i ciągłość kątów obrotu

$$\text{ugięcia} \quad u_3^e = u^{e+1}_1, \quad \text{obrót} \quad u_4^e = u_2^{e+1}$$

• warunki równowagi sił przekrojowych (siły poprzeczne i momenty gnące)

$$\text{siła poprzeczna} \quad Q_3^e + Q^{e+1}_1 = 0, \quad \text{moment zginający} \quad Q_4^e = Q_2^{e+1} = 0$$

W przypadku gdy w węźle jest przyłożony siła skupiona lub moment zginająca mamy

$$\text{siła poprzeczna} \quad Q_3^e + Q^{e+1}_1 = P, \quad \text{moment zginający} \quad Q_4^e = Q_2^{e+1} = M$$

Wprowadźmy globalną numerację przemieszczeń węzłowych

$$u_1^1 = U_1, u_2^1=U_2, \quad u_3^1 = u_1^2 = U_3, \quad u_4^1 = u_2^2 = U_4, ..., \quad u_4^N = U_{4(N+1)}$$

Następnie krokiem jest budowa globalnej macierzy sztywności i globalnego wektora obciążenia (analogiczne do przykładu jednowymiarowego

$$\mathbf{K} \mathbf{U} = \mathbf{F}$$

gdzie $\mathbf{F}$ jest wektorem który zawiera obciążenia zewnętrzne i obciążenia węzłowe. Powyższy układ równań będzie zawierał $2(N+1)$ niewiadomych przemieszczeń węzłowych gdzie $N$ - oznacza liczbę elementów. W każdym węźle poszukujemy ugięcia i kąta obrotu.

Uwzględnienie warunków brzegowych

Podobnie jak dla przykładu jednowymiarowego znane ugięcia i kąty obrotu wstawiamy do wektora $\mathbf{U}$, natomiast obciążenie ciągłe i skupione do wektora $\mathbf{F}$