Element kratowy 2D
W przypadku kratownicy (układu prętowego wykonanego z prętów połączonych przegubowo i przenoszących tylko rozciąganie bądź ściskanie) przemieszczenia węzłowe i siły węzłowe wygodnie jest przedstawić w każdym węźle za pomocą dwóch składowych w układzie lokalnym. Lokalny układ współrzędnych posłuży nam do budowania macierzy sztywności a globalny do definiowania całej konstrukcji.
Dyskretyzacja
Każdy pręt kratownicy traktujemy jako jeden element skończony
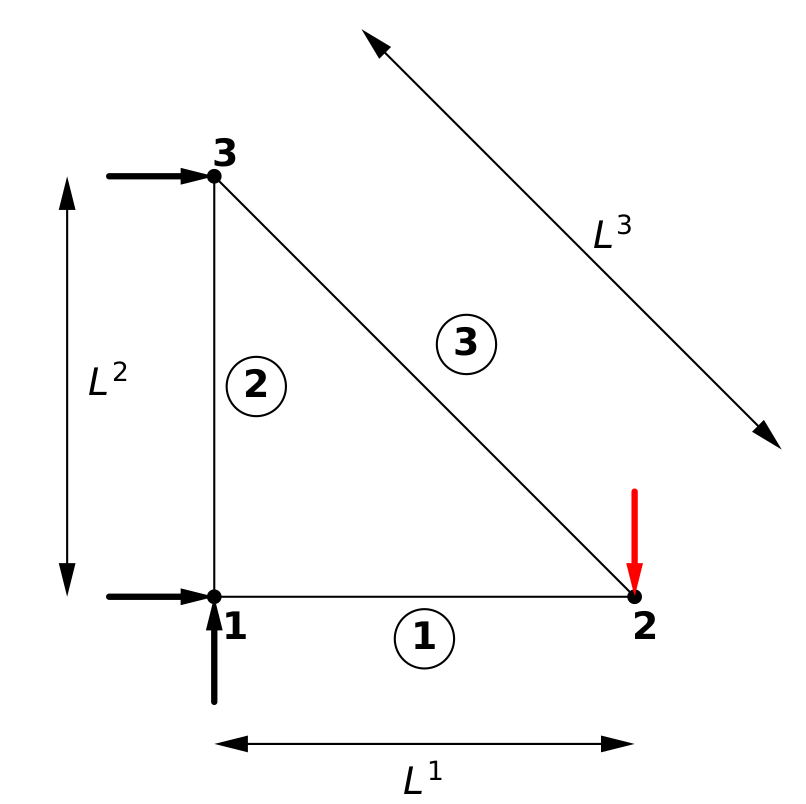
Równanie opisujące element skończony
Wybierzemy z kratownicy jeden element skończony który jest nachylony pod kątem $\alpha$.
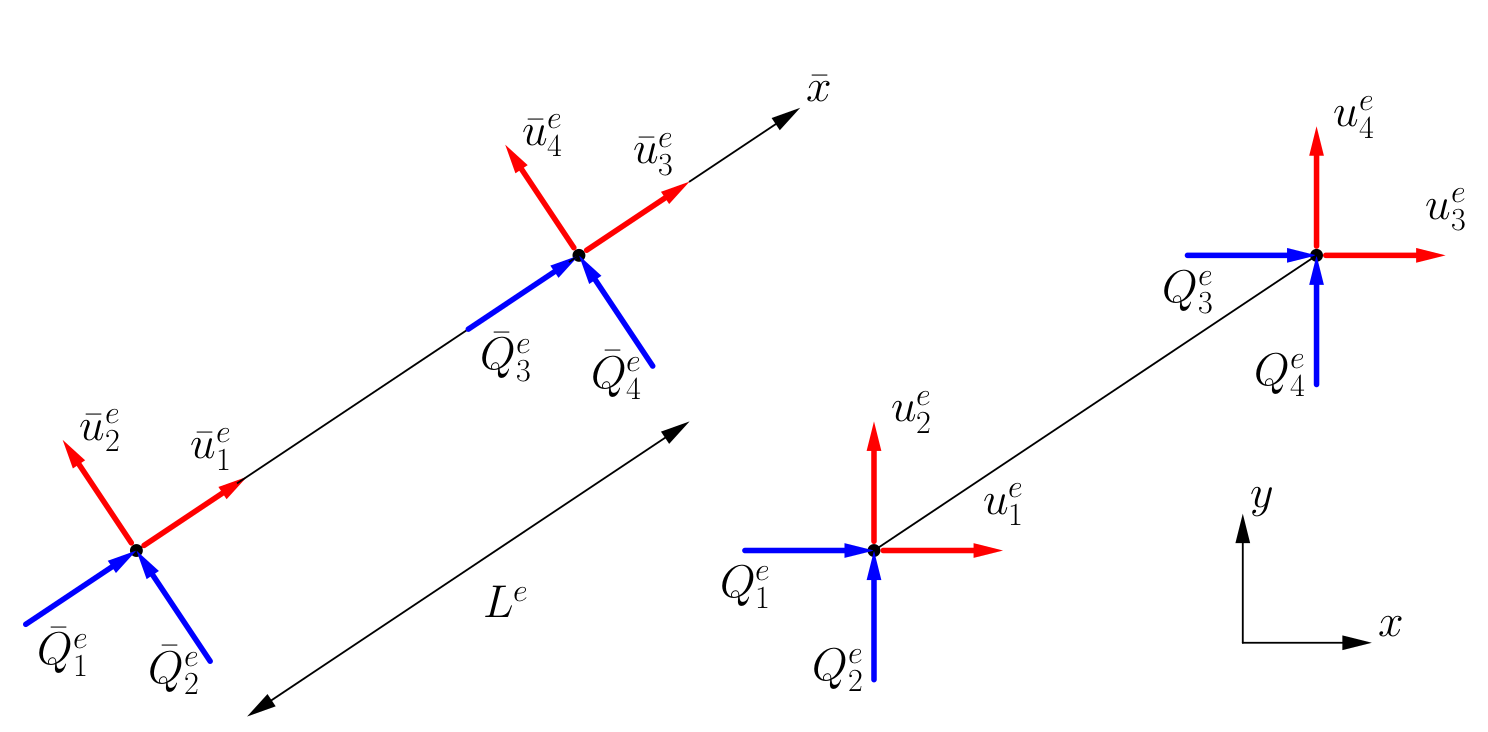
Zapiszmy macierz sztywności, wektor obciążeń węzłowych oraz wektor przemieszczeń węzłowych dla elementu kratowego z dwoma stopniami swobody
$$\mathbf{\bar{k}}^e =\cfrac{EA}{L^e} \begin{bmatrix} 1 & 0 & -1 & 0\\ 0 & 0 & 0 & 0\\ -1 & 0 & 1 & 0\\ 0 & 0 & 0 & 0\\ \end{bmatrix} \quad \mathbf{\bar{Q}}^e = \begin{bmatrix} \bar{Q}_1^e\\ 0\\ \bar{Q}_3^e\\ 0\\ \end{bmatrix} \quad \mathbf{\bar{u}}^e = \begin{bmatrix} \bar{u}_1^e\\ 0\\ \bar{u}_3^e\\ 0\\ \end{bmatrix}$$Nie uwzględniamy wektora sił zewnętrznych $\f^e$ gdyż w kratownicy zakładamy, ze obciążenie jest przykładane wyłącznie do węzłów. Aby otrzymać macierz w globalnym układzie współrzędnych musimy dokonać transformacji. Macierz transformacji ma następującą postać
$$\T^e = \matt{\t^e}{\mathbf{0}}{\mathbf{0}}{\t^e}, \quad \T^e = \matt{\cos\alpha^e}{\sin\alpha^e}{-\sin\alpha^e}{\cos \alpha^e}$$Kąt $\alpha^e$ jest kątem transformacji o dodatnim znaku. Stosując prawo transformacji dostajemy macierze sztywności jako
$$\boldsymbol{k} = (\T^e)^T\bar{\boldsymbol{k}}^e \T^e$$podobnie dla wektora siła węzłowych i przemieszeń węzłowych
$$\mathbf{Q}^e = (\T^e)^T \mathbf{\bar{Q}}^e, \quad \mathbf{u} = (\T^e)^T \mathbf{\bar{u}}$$Wykonując powyższe operacje dostajemy równanie
$$\mathbf{k}^e \mathbf{u}^e = \mathbf{Q}^e$$gdzie
$$\boldsymbol{k}^e = \cfrac{EA}{L^e} \begin{bmatrix} \cos^2\alpha & \cos \alpha \sin \alpha & -\cos^2 \alpha & -\cos \alpha \sin \alpha \\ \cos \alpha \sin \alpha & \sin^2 \alpha & -\cos \alpha \sin \alpha & -\sin^2 \alpha \\ -\cos^2 \alpha & -\cos \alpha \sin \alpha & \cos^2 \alpha & \cos \alpha \sin \alpha \\ -\cos \alpha \sin \alpha & -\sin^2 \alpha & \cos \alpha \sin \alpha & \sin^2 \alpha \\ \end{bmatrix} \quad \mathbf{u}^e = \begin{bmatrix} u_1^e\\ u_2^e\\ u_3^e\\ u_4^e\\ \end{bmatrix} \quad \mathbf{Q}^e= \begin{bmatrix} Q_1^e\\ Q_2^e\\ Q_3^e\\ Q_4^e\\ \end{bmatrix}$$