Wprowadzenie do metody elementów skończonych

• Metoda elementów skończonych (MES) jest jedną z najbardziej popularnych metod komputerowych służących do rozwiązywania zagadnień mechaniki.
• Istotą MES jest zastąpienie równań różniczkowych opisujących dany problem brzegowym układem równań algebraicznych.

Metoda elementów skończonych jest realizowana w następujących etapach
• podziała obszaru na podobszary (elementy skończone) Proces ten nazywamy dyskretyzacja. Obszary powinny być proste (trójką, kwadrat, prostopadłościan)
• budowa elementu skończonego
• proces agregacji (złożenie)
• uwzględnienie warunków brzegowych
• rozwiązanie układu równań algebraicznych
• obliczenie dodatkowych wielkości (odkształcenie, naprężenie, siła)

Rozciąganie pręta

$$EA\cfrac{d^2u(x)}{dx^2} + q = 0$$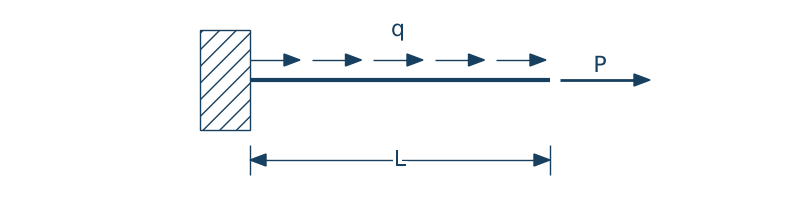

Dyskretyzacja pręta

Podzielmy nasz obszar $\Omega$ na pewne podobszary który nazywać będziemy elementami skończonymi. Załóżmy więc, że obszar $\Omega$ zawarty między punktami $a$ i $b$, gdzie $a \leq x\leq b$ , został podzielony na $n$ podobszarów (elementów), tak jak to pokazano na rysunku. Oznaczmy przez $\Omega^{e}$ gdzie $e$ zmienia się od $1$ do $n$ obszar zajmowany przez jeden element skończony. Punkty wyznaczające podział na elementy skończone będziemy nazywać węzłami. Zbiór wszystkich elementów skończonych będziemy nazywać siatką elementów skończonych.

$$\Omega = \Omega^1 \cup \Omega^2 \cup ... \cup \Omega^n.$$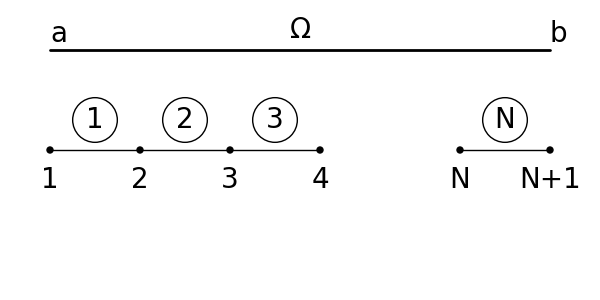

Każdy element jest ograniczony dwoma węzłami. Całkowita liczba węzłów w rozpatrywanym przypadku wynosi $N+1$.

Równania opisujące element skończony

Przeanalizujmy zatem element o dwóch węzłach w punktach $x_1$ i $x_2$. Niech na obszarze elementu zmiana tej wielkości będzie opisana za pomocą zależności

$$u^e(x) = u_1^e N_1^e(x)+ u_2^e N_2^e(x)$$

gdzie funkcje $N_1$ i $N_2$ mają postać

$$N_1^e = \cfrac{x_2-x}{x_2-x_1}, \qquad N_2^e = \cfrac{x-x_1}{x_2-x_1}$$

Parametry $u_1^e$ i $u_2^e$ są nieznanymi przemieszczeniami węzłowymi.

Rozwiązanie na elemencie może zapisać w formie macierzowej jako

$$u^e(x) = \N\u, \quad \N = [ N_1^e, N_2^2], \quad \mathbf{u} = [u_1^e, u_2^e]^T$$

Wektor $\mathbf{u}$ jest wektorem kolumnowym tak aby można było wykonać mnożenie macierzowe (iloczyn skalarny). Dwuelementowa macierz $\N^e$ gromadzi funkcje kształtu, a wektor zawiera wartości zmiennych pola punktach węzłowych. Wektor $\u$ zawiera nieznane przemieszczenia węzłowe. Wystawy nasze przybliżone rozwiązanie do naszego równania różniczkowego. W następnym kroku równanie przemnażamy \textbf{lewostronnie} przez $\N^T$ i całkujemy po obszarze rozważanego elementu skończonego.

$$EA\cfrac{d^2}{dx^2}\mathbf{N}\mathbf{u} + q(x) = 0 \qquad |\int \cdot \mathbf{N}^T$$

W metodzie Galerkina minimalizacja reziduum odbywa się przez przemnożenie równanie przez funkcję testową i wyliczeniu całki na obszarze czyli

$$\int_{x_1}^{x_2} \mathbf{N}^TEA\cfrac{d^2\mathbf{N}}{dx^2}\mathbf{u} dx + \int_{x_1}^{x_2}\mathbf{N}^Tq(x) dx = 0$$

Powyższy zapis oznacza, że dostajemy dwa równania bo mamy dwie funkcje. Dlatego mnożymy przez $\mathbf{N}^T$ inaczej nie dostalibyśmy dwóch równań. Ma być tyle równań ile funkcji kształtu na danym elemencie.

Zastosujmy całkowanie przez części i przemnóżmy przez -1:

$$\int f(x) \cdot g{'}(x) dx = f(x) \cdot g(x) - \int f{'}(x) \cdot g(x) dx$$

czyli $f(x) = \mathbf{N}^T, \, g(x) = \cfrac{d \N}{dx}$

$$\int_{x_1}^{x_2} EA \cfrac{d\mathbf{N}^T}{dx}\cfrac{d\mathbf{N}}{dx} dx\mathbf{u}-\int_{x_1}^{x_2} \mathbf{N}^T q(x) dx - EA\mathbf{N}^T\cfrac{d\mathbf{N}}{dx}\mathbf{u}|_{x=x_2} + EA\mathbf{N}^T\cfrac{d\mathbf{N}}{dx}\mathbf{u}|_{x=x_1}=0$$

Powyższe równanie nosi nazwę sformułowania słabego lub wariacyjnego. Słowo słaby odnosi się do faktu, że obniżone zostały wymagania co do różniczkowalności funkcji przemieszczenia $u(x)$. Przepiszmy powyższe równanie stosują następujące oznaczenia

$$\K^e = \int_{x_1}^{x_2} EA \cfrac{ d\mathbf{N}^T}{dx} \cfrac{d\mathbf{N}}{dx} dx$$ $$\mathbf{f}_{\mathbf{2\times 2}}^e = \int_{x_1}^{x_2} \mathbf{N}^T q(x) dx$$ $$\mathbf{Q}_{\mathbf{2\times 2}}^e = EA\mathbf{N}^T\cfrac{d\mathbf{N}}{dx}\mathbf{u}|_{x=x_2} - EA\mathbf{N}^T\cfrac{d\mathbf{N}}{dx}\mathbf{u}|_{x=x_1}$$ $$\K_{\mathbf{2\times 2}}^e \mathbf{u_{2\times 1}} = \mathbf{f}_{\mathbf{2\times 1}}^e + \mathbf{Q}_{\mathbf{2\times 1}}^e$$

Zajmijmy się teraz pierwsza całką (lokalna macierze sztywności elementu skończonego) Długośc elementu skończonego oznaczmy jako $L$

$$k_{11}^e = \int_{x_1}^{x_2} EA \cfrac{dN_1}{dx}\cfrac{dN_1}{dx} dx = EA\int_{x_1}^{x_2} -\cfrac{1}{x_2-x_1} \cdot \left(-\cfrac{1}{x_2-x_1}\right) dx =$$ $$k_{11} = EA \cfrac{x}{(x_2-x_1)^2}|_{x_1}^{x_2} = EA \left(\cfrac{x_2}{(x_2-x_1)^2}- \cfrac{x_1}{(x_2-x_1)^2}\right) = EA \cfrac{x_2-x_1}{(x_2-x_1)^2} = \cfrac{EA}{x_2-x_1} = \cfrac{EA}{L^e}$$ $$k_{12} = -\cfrac{EA}{L^e}$$

gdzie $L^e$ - jest długością rozważanego elementu skończonego.

$$\mathbf{k}_{\mathbf{2\times 2}}^e = \cfrac{EA}{L^e} \matt{1}{-1}{-1}{1}$$

Rozpatrzymy teraz drugą całkę czyli $\f^e$

$$f_1^e = \int_{x_1}^{x_2} N_1(x) q dx = \cfrac{1}{2}qL^e, \qquad f_2^e = \int_{x_1}^{x_2} N_2(x) q dx = \cfrac{1}{2}qL^e$$

stosując zapis macierzowy dostajemy

$$\mathbf{f}_{\mathbf{2\times 1}}^e = \cfrac{1}{2}qL^e\vcc{1}{1}$$

Zajmijmy się teraz wektorom sił węzłowych przyjmują oznaczenia

$$Q_2 = EA\cfrac{d\mathbf{N}}{dx}\u|_{x=x_2}, \qquad Q_1 =-EA\cfrac{d\mathbf{N}}{dx}\u|_{x=x_1}$$

czyli mamy

$$= \mathbf{N}^T(x_2)Q_2 + \mathbf{N}^T(x_1)Q_1 = \vcc{0}{1}Q_2 + \vcc{1}{0}Q_1 =\vcc{Q_1}{Q_2}$$

• $\K^e$ - symetryczna macierz kwadratowa (macierz sztywności elementu skończonego $\Omega^e$
• $\mathbf{u}$ - wektor kolumnowy przemieszczeń węzłowych elementu
• $\mathbf{f}^e$ - wektor kolumnowy obciążeń ciągłych elementu
• $\mathbf{Q}^e$ - wektor kolumnowy sił węzłowych elementu.

Agregacja elementów skończonych

Do tej pory nasze rozważania dotyczyły wyłącznie jednego elementu skończonego. Spróbujmy teraz podzielić naszą konstrukcję na $n$ elementów skończonych. Rozpatrzmy dwa sąsiednie elementy $\Omega^e$ oraz $\Omega^{e+1}$

• warunki ciągłości przemieszczeń w węzłach

$$u_2^e = u_1^{e+1}$$

• warunki równowagi sił w węzłach

$$Q_2^e + Q_1^{e+1} = 0$$

jeżeli w punkcie przyłożona jest siła zewnętrzna to wtedy

$$Q_2^e + Q_1^{e+1} = P$$

Uwaga. Jeżeli na długości pręta pojawiają się jakieś obciążenia skupione to aby je uwzględnić musimy wstawić tam węzły

Wprowadźmy globalną numerację przemieszczeń węzłowych

$$u_1^1 = U_1, \quad u_2^1 = u_1^2 = U_2, \quad u_2^2 = u_1^3 = U_3, ..., \quad u_2^{N-1} = u_1^N = U_N, \quad u_2^N = U_{N+1}$$

Rozpiszmy nasze równania na elemencie używając nowych oznaczeń
• 1) $k_{11}^1 U_1 + k_{12}^1U_2 = f_1^1 + Q_1^1$
• 2)$k_{21}^1 U_1 + k_{22}^1U_2 = f_2^1 + Q_2^1$
• 3) $k_{11}^2 U_2 + k_{12}^2 U_3 = f_1^2 + Q_1^2$
• 4) $k_{21}^2 U_2 + k_{22}^2U_3 = f_2^2 + Q_2^2$
• $\vdots$

• 2N) $k_{21}^N U_N + k_{22}^NU_{N+1} = f_2^N + Q_2^N$

Wykorzystajmy warunki równowagi czyli dodajmy do równania 2) równanie 3). Pierwsze i ostatnie równanie będzie bez zmian. Czyli nasza liczba równań będzie równa $1+1 + (2n-2)/2 = n+1$.

• 1) $\quad k_{11}^1 U_1 + k_{12}^1U_2 = f_1^1 + Q_1^1 \quad \text{bez zmian}$
• 2) $\quad k_{21}^1 U_1 + k_{22}^1U_2 \quad k_{11}^2 U_2 + k_{12}^2 U_3 = f_2^1 + Q_2^1 + f_1^2 + Q_1^2$
• 3) $\quad k_{21}^1 U_1 + k_{22}^1U_2 \quad k_{11}^2 U_2 + k_{12}^2 U_3 = f_2^1 + Q_2^1 + f_1^2 + Q_1^2$
• 4) $\quad k_{21}^1 U_1 + (k_{22}^1 \quad k_{11}^2) U_2 + k_{12}^2 U_3 = f_2^1 + Q_2^1 + f_1^2 + Q_1^2$
• N+1) $\quad k_{21}^N U_N + k_{22}^NU_{N+1} = f_2^N + Q_2^N \quad \text{bez zmian}$

Powyższy układ równań liniowych możemy zapisać w formie macierzowej jako

$$\begin{bmatrix} k_{11}^1 & k_{12}^1 & 0 & 0 & \ldots & 0 \\k_{21}^1 & k_{22}^1+k_{11}^2 & k_{12}^2 & 0 & \ldots & 0 \\ E0 & k_{21}^2 & k_{22}^2+k_{11}^3 & & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & k_{22}^N \\\end{bmatrix}\begin{bmatrix} U_1 \\U_2\\ U_3\\ \vdots \\ U_{n+1}\\\end{bmatrix}=\begin{bmatrix} f_1^1 \\f_2^1+f_1^2\\ f_2^2+f_1^3 \\ \vdots \\ f_2^N\\\end{bmatrix}\begin{bmatrix} Q_1^1 \\Q_2^1+Q_1^2\\ Q_2^2+Q_1^3 \\ \vdots \\ Q_2^N\\\end{bmatrix}$$

czyli

$$\K \mathbf{U} = \mathbf{F}$$

Uwzględnienie warunków brzegowych

Układ równań wyprowadzony w poprzedniej sekcji nie zawiera warunków brzegowych. Globalna macierz sztywności jest osobliwa bo wymaga uwzględnienia podstawowych warunków brzegowych. Z kolei wektor prawej strony zawiera również nieznane informacje o siłach reakcji. Nasz układ możemy przestawić w postaci

$$\begin{bmatrix} \K^{11} & \K^{12} \\\K^{21} & \K^{22} \\ \end{bmatrix}\begin{bmatrix} \mathbf{U}^{1}\\\mathbf{U}^{2}\\ \end{bmatrix}=\begin{bmatrix} \mathbf{F}^{1}\\\mathbf{F}^{2}\\ \end{bmatrix}$$

gdzie
• $\mathbf{U}^1$ zawiera zadane przemieszczeni węzłowe zadane przez warunki brzegowe (podpory)
• $\mathbf{U}^2$ zawiera nieznane przemieszczenie węzłowe
• $\mathbf{F}^1$ jest wektorem nieznanych obciążeń (siły reakcji)
• $\mathbf{F}^2$ jest znanym wektorem obciążeń zewnętrznych

Zapiszmy nasze równanie w postaci dwóch równań

$$\K^{11}\mathbf{U}^{1} +\K^{12}\mathbf{U}^{2} = \mathbf{F}^{1}$$ $$\K^{21}\mathbf{U}^{1} +\K^{22}\mathbf{U}^{2} = \mathbf{F}^{2}$$

Z drugiego równania możemy wyznaczyć nieznane przemieszenia węzłowe jako

$$\mathbf{U}^{2} = \left(\K^{22}\right)^{-1}(\mathbf{F}^{2}-\K^{21}\mathbf{U}^{1})$$

Znając $\mathbf{U}^{2}$ możemy wyznaczyć nieznane obciążenie $\mathbf{F}^{1}$

Odkształcenie, naprężenie, siła

Po obliczeniu niewiadomych przemieszczeń w węzłach w następnym kroku przechodzimy do wyznaczania odkształcenia, naprężenia i siły. Przemieszczenie dowolnego punktu leżącego na osi pręta obliczamy jako

$$u(x) = u_1^eN_1^e(x) + u_2^eN_2^e(x) \quad \text{dla} \quad x\in \Omega^e$$

Odkształcenie jest w każdym elemencie stałe z uwagi na fakt przyjęcia liniowych funkcji kształtu.

$$\varepsilon(x) = u_1^e\cfrac{N_1^e(x)}{dx} + u_2^e\cfrac{N_2^e(x)}{dx} \quad \text{dla} \quad x\in \Omega^e$$

Naprężenie i siłę wyznaczamy w analogiczny sposób przemnażając odkształcenia przez $E$ w przypadku naprężeń oraz $EA$ w przypadku sił.

$$\sigma(x) = E \varepsilon(x), \qquad F(x) = A\sigma(x)$$