Metody aproksymacyjnego rozwiązywania równań różniczkowych

Zapiszmy jeszcze raz równanie różniczkowe w ogólnej postaci wraz z jednorodnymi warunkami brzegowymi. Jednorodne warunki brzegowe to takie które są równe zero.

$$F(u(x)) = 0, \quad x \in \Omega=[a,b], \quad u(x=a) = 0 \qquad u(x=b) = 0$$

Przyjmijmy, że rozwiązanie równania różniczkowego jest w postaci:

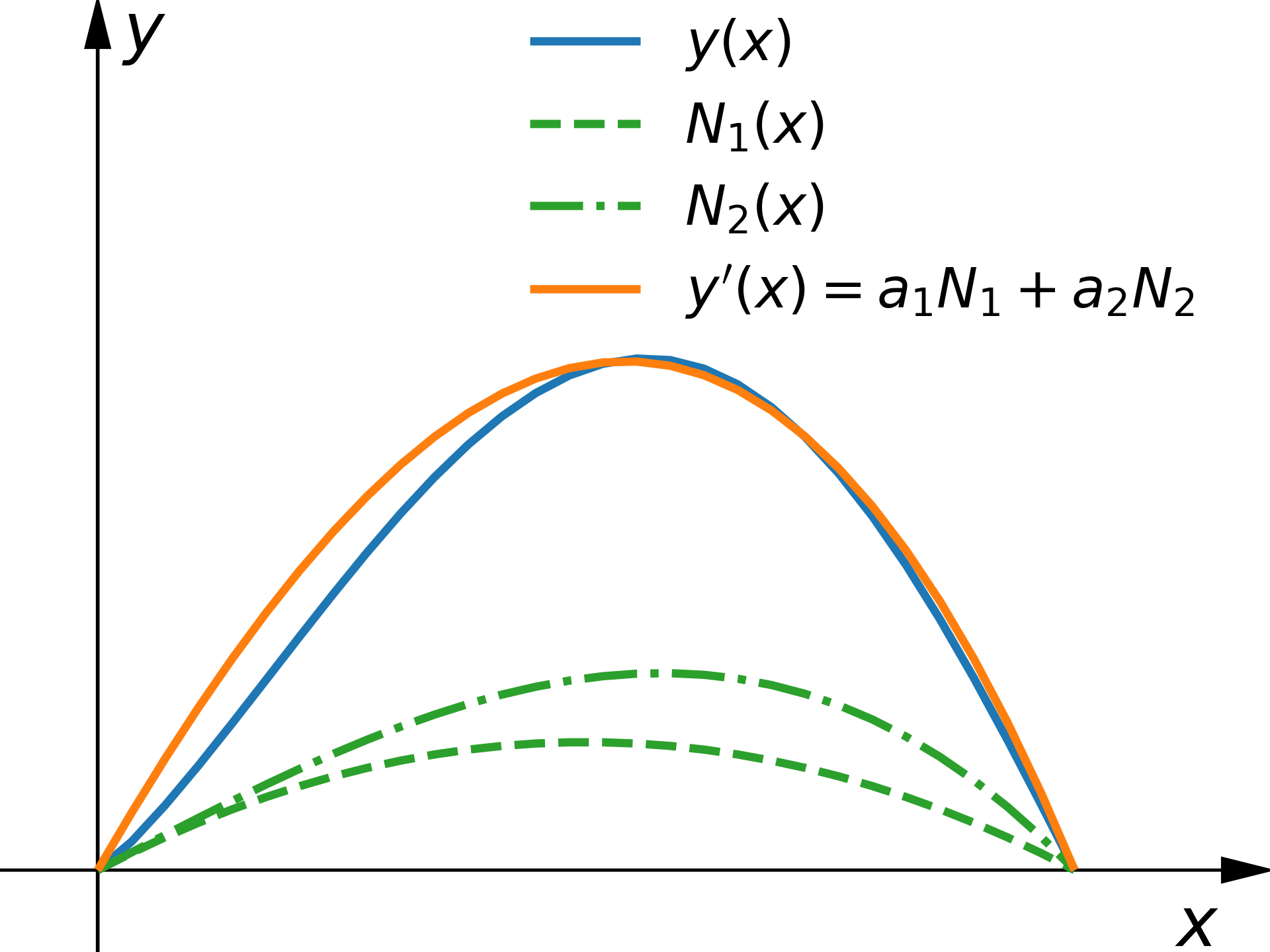
$$u{'} = u{'}(x,a_1,a_2,...,a_3) = \sum_{i=1}^{n}a_i \cdot N_i(x)$$

Funkcje $N_i$ nazywamy funkcjami próbnymi. Funkcje te muszą spełniać warunki brzegowe. Problem redukuje się więc do trafnego wyboru funkcji próbnych i znalezienia parametrów $a_i$, $N_i$ = funkcje próbne, testowe, (eng. trial function)

Przyjmowane funkcje muszą być ciągłe i różniczkowalne do najwyższego rzędu występującego w całkowej formie równania. Różnicę między rozwiązaniem dokładnym a przybliżonym oznaczmy jako reziduum ( "reszta")

$$F(u{'}(x,a_i)) = R(x,a_i).$$

Rezidua $R$ zależą od $x$ oraz $a_i$. Jeżeli przyjęta aproksymacja prowadzi do $R = 0$ dla wszystkich punktów obszaru $\Omega$ to jest to wtedy rozwiązanie dokładne . W ogólności $R$ jest różne od zera, jakkolwiek w wybranych punktach obszaru $\Omega$ warunek ten może być spełniony.

Metoda ważonych reziduów

Metody ważonych reziduów zakładają wyznaczenie nieznanych parametrów $a_i$ przez spełnienie określonego warunku:

$$\int_{\Omega}w(x) R(x,a_i) d\Omega = 0, \quad \text{dla} \quad i=1,2,...,n,$$

gdzie funkcja $w(x)$ jest tzw. funkcja wagowa. Różny wybór funkcji wagowych pozwala określa różne wersje tej metody.

Metoda punktu kolokacji

W metodzie punktu kolokacji role funkcji wagowych pełnią $w_i(x) = \delta(x-x_i)$, gdzie $\delta$ pełni funkcję delty Diraca, która jest zdefiniowana następująco:

$$\delta(x) = \infty \text{ dla } x=0, \qquad \delta(x) = 0 \text{ dla } x \neq 0, \qquad \int_{-\infty}^{\infty} \delta(x) dx = 1$$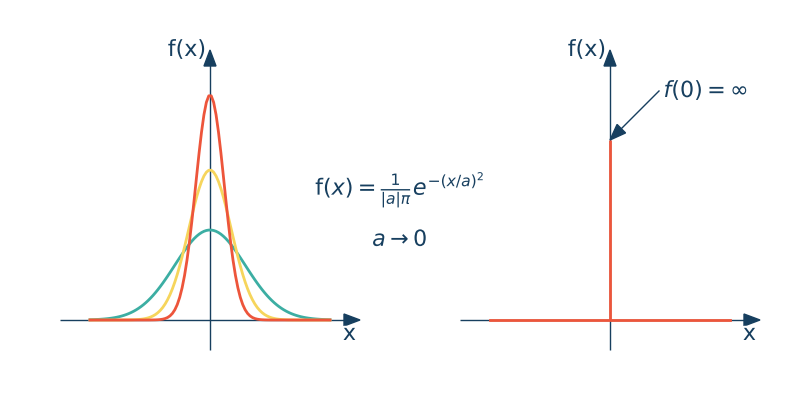

Warunek z użyciem tej wagi wygląda następująco

$$\int_{\Omega}\delta(x-x_i) R(x,a_i) d\Omega = 0, \quad \text{dla} \quad \, i=1,2,...,n,$$

Formułując ten warunek w $n$ punktach $x_i$ , otrzymujemy układ równań algebraicznych, z którego wyznaczymy niewiadome $a_i$.

Metoda podobszarów kolokacji

Funkcje wagi w tej metodzie dobiera się w taki sposób, że ich wartości są równe $1$ w danej części obszaru , natomiast na pozostałej części obszaru $\Omega$ są równe zeru. Podobszarów kolokacji definiuje się tyle, ile jest przyjętych funkcji próbnych.

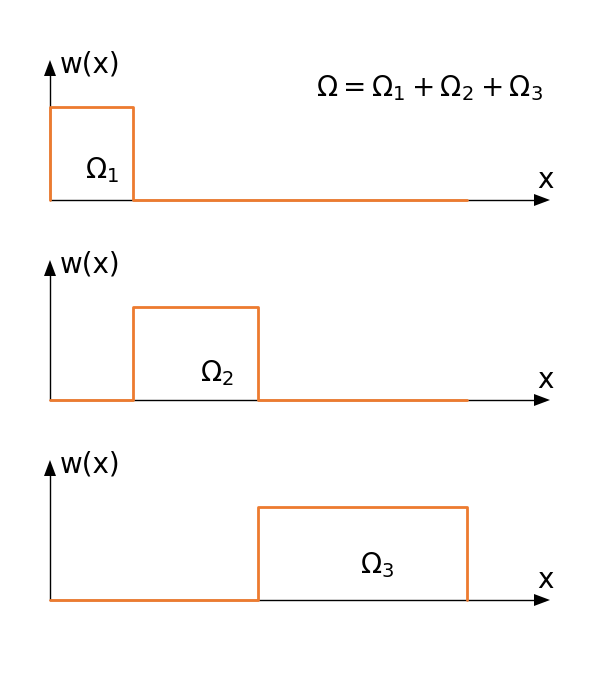
Funkcje wag w poszczególnych podobszarach możemy zapisać jako

$$w_1(x)=\begin{cases}1,& x\in\Omega_1\\0,& x\not\in \Omega_1\end{cases}$$ $$w_2(x)=\begin{cases}1,& x\in\Omega_2\\0,& x\not\in \Omega_2\end{cases}$$ $$w_3(x)=\begin{cases}1,& x\in\Omega_3\\0,& x\not\in \Omega_3\end{cases}$$

Metoda najmniejszych kwadratów

Metoda najmniejszych kwadratów polega na zminimalizowaniu wyrażenia

$$I = \int_{\Omega}R^2(x,a_i) d\Omega.$$

Aby wartość $I$ była minimalna ze względu na nieznane parametry $a_i$ dokonujemy różniczkowania po tych parametrach i wynik przyrównujemy do zera. Otrzymujemy następujący układ równań

$$\pp{I}{a_1} = \pp{}{a_1}\int_{\Omega} R^2 dx = \int_{\Omega}\pp{}{a_1} R^2 dx = \int_{\Omega} R \pp{R}{a_1} dx = 0$$ $$\pp{I}{a_2} = \pp{}{a_2}\int_{\Omega} R^2 dx = \int_{\Omega}\pp{}{a_2} R^2 dx = \int_{\Omega} R \pp{R}{a_2} dx = 0\vdots$$ $$\pp{I}{a_n} = \pp{}{a_n}\int_{\Omega} R^2 dx = \int_{\Omega}\pp{}{a_n} R^2 dx = \int_{\Omega} R \pp{R}{a_n} dx = 0$$

Porównując otrzymane równania z ogólnym równanie metody ważonych reziduów widać, że role funkcji wagowych pełnią pochodne reziduów

$$w_i(x) = \pp{R}{a_i}, \quad \text{dla} \quad i=1,2,...,n$$

Metoda Galerkina

Metoda Galerkina zakłada, że rolę funkcji wagowych pełnią przyjmowane funkcja próbne a więc, że $w_i(x)=N_i(x)$: Ogólne równanie tej metody może zapisać jako

$$\int_{\Omega}N_i(x)R(x,a_i) d\Omega = 0 \qquad \text{dla} \quad i=1,2,...,n.$$

Dostajemy $n$ równań z których jesteśmy wstanie wyliczyć nieznane współczynniki $a_i$.

Metoda wariacyjna Rayleigha-Ritza

Funkcjonał jako analogia do funkcji. Argumentem funkcjonału są są funkcje a zbiorem wartości liczby rzeczywiste.

$$\mathcal{R} \rightarrow f(x) \rightarrow \mathcal{R},\qquad f(x) \rightarrow J(f(x)) \rightarrow \mathcal{R}$$

Typowy problem jednowymiarowego rachunku wariacyjnego polega na znalezieniu takiej funkcji $f(x)$, by zminimalizować bądź zmaksymalizować całkę:

$$I(u(x)) = \int_a^bF(u(x)) dx$$

gdzie $I$ jest funkcjonałem, funkcją której argumentem są funkcje. Problem minimalizacji możemy zapisać jako

$$\delta I(u(x)) = 0$$

czyli wariacja funkcjonału $I$ musi być równa zero. W metodzie Rayleigha-Ritza rozwiązanie przybliżane jest stosując następujące podstawienie

$$u(x) \approx u{'} = u{'}(x,a_1,a_2,...,a_3) = \sum_{i=1}^{n}a_i \cdot N_i(x)$$

Wstawiaj przybliżone rozwiązanie do funkcjonału możemy zapisać

$$I(T'(x)) = I(x, a_1, a_2,..., a_n)$$

Nasz funkcjonał zależny jest wiec od nieznanych współczynników.
Nieznany parametry są wyznaczane z następującego równania

$$\delta I = 0 =\pp{I}{a_1}\delta a_1 + \pp{I}{a_2}\delta a_2 + ,...,\pp{I}{a_n}\delta a_n.$$

Parametry $a_i$ są od siebie niezależne czyli każdy człon w równaniu musi być równy $0$. Dostajemy wiec układ równań na nieznane parametry

$$\pp{I}{a_i} = 0, \quad \text{dla} \quad i=1,2,...,n$$

Jak wyznaczyć funkcjonał dla danego równania różniczkowego

Sformułowanie słabe jest konstruowane w czterech krokach:
• Przemnożenie równania różniczkowego przez dowolną funkcję.
• Przecałkowanie wyniku po rozważanym obszarze $\Omega$.
• Całkowanie przez części z wykorzystaniem twierdzenia Greena-Gaussa w celu zredukowania pochodnych do minimalnego rzędu.
• Wprowadzenie do funkcjonału warunków brzegowych Neumanna.

Wyprowadźmy równanie słabe dla zagadnienia przepływu ciepła w pręcie

$$kA \cfrac{d^2T}{dx^2} + f(x) = 0, \quad 0\leq x \leq l$$

Mnożąc powyższe równanie stronami przez wariację $\delta T(x)$ poszukiwanej funkcji która jest dowolną funkcją ciągłą spełniającą warunki brzegowe dostajemy

$$kA \cfrac{d^2T}{dx^2}\delta T(x) + f(x)\delta T(x) \ = 0$$

Przecałkujmy równanie w zadanym przedziale

$$\int_0^l kA \cfrac{d^2T}{dx^2}\delta T(x) dx + \int_0^lf(x)\delta T(x)dx \ = 0$$

Całkując pierwszy składnik przez części dostajemy

$$\int_0^l kA \cfrac{d^2T}{dx^2}\delta T(x) dx = kA \cfrac{T(x)}{dx}\delta T(x)|_0^l - kA\int_0^l \cfrac{T(x)}{dx}\cfrac{\delta T(x)}{dx} dx$$

Wystawy go do naszego równani i przemnóżmy przez -1.

$$kA\int_0^l \cfrac{T(x)}{dx}\cfrac{\delta T(x)}{dx} dx - kA \cfrac{T(x)}{dx}\delta T(x)|_0^l - \int_0^l f(x) \delta T(x) dx = 0$$

Rozpiszmy granice całkowania

$$kA\int_0^l \cfrac{T(x)}{dx}\cfrac{\delta T(x)}{dx} dx - \int_0^lf(x) \delta T(x) dx + kA \cfrac{T(0)}{dx}\delta T(0) - kA \cfrac{T(l)}{dx}\delta T(l) = 0$$

Powyższą zależność nazywamy sformułowaniem słabym. Równanie to możemy zapisać jako wariacja pewnego funkcjonału $I$ czyli

$$\delta I(T) = 0$$

gdzie

$$I(T) = \int_0^l \left( \cfrac{1}{2}kA\cfrac{T(x)}{dx}\cfrac{T(x)}{dx} - f(x) T(x)\right) dx + kA \cfrac{T(0)}{dx}T(0) - kA \cfrac{T(l)}{dx}T(l)$$

Uwaga, w wzorze na funkcjonał dodaliśmy $1/2$ który wynika z obliczania wariacji funkcjonału, ($x^2->2x$). W przypadku rozciąganego pręta $I$ opisuje energię potencjalną belki. Pierwsza całka w powyższych funkcjonale oznacza energię odkształcenia, zaś pozostałe składniki wyrażają pracę (potencjał) sił zewnętrznych.