Równania różniczkowe zwyczajne wyższych rzędów - układ równań

Zapiszmy równanie różniczkowe zwyczajne w ogólnej postaci. Równanie jest rzędu $k$. O tym któreo rzędu jest równanie różniczkowego decyduje najwyższy rząd pochodnej występujący w równaniu.

$$\cfrac{d^ky}{dy^k} = F\left(x,y, \cfrac{dy}{dx}, ..., \cfrac{d^{k-1}y}{dx^{k-1}}\right)$$

Zastosujmy proste podstawienie

$$y = z_1, \quad \cfrac{dz_1}{dx} = z_2, \quad \cfrac{dz_2}{dx} = z_3, \quad \cfrac{dz_k}{dx} = F(x,z_1,..., z_k)$$

W ogólnym przypadku możemy zapisać

$$y=z_1, \quad \cfrac{dz_j}{dx} = z_{j+1}, \text{dla} \quad j=1,...,k-1$$

Dostajemy więc $k$ równań różniczkowych. Powyższy układ równań musimy uzupełnić o warunki początkowe. Przypomnijmy, że liczba warunków początkowych musi odpowiadać rzędowi równania różniczkowego a więc

$$z_1(x_0) = y(x_0), \qquad z_2(x_0) = \cfrac{dy}{dx}|_{x_0}, \ldots, z_k(x_0) = \cfrac{d^{k-1}y}{dx^{k-1}}|_{x_0}$$

Przykład: Wyznaczyć funkcję ugięcia i kąta obrotu w belce wspornikowej obciążonej siła skupioną.
Równanie różniczkowe jest następujące

$$\cfrac{d^2w(x)}{dx^2} = -\cfrac{M(x)}{EI(x)},$$

Równanie zamieniamy na tożsamy układ równań różniczkowych pierwszego rzędu.

$$\cfrac{dw(x)}{dx} = \theta(x), \quad \cfrac{d\theta(x)}{dx} = -\cfrac{M(x)}{EI(x)},$$

+ warunki początkowe $w(x=0)=0, \theta(x=0)=0$

Metoda strzałów

Metoda rozwiązywania zagadnienia brzegowego przez zastąpienie go zagadnieniem początkowym. Pokażmy jak działa ta metoda na przykładzie belki swobodnie podpartej z obciążeniem ciągłym.

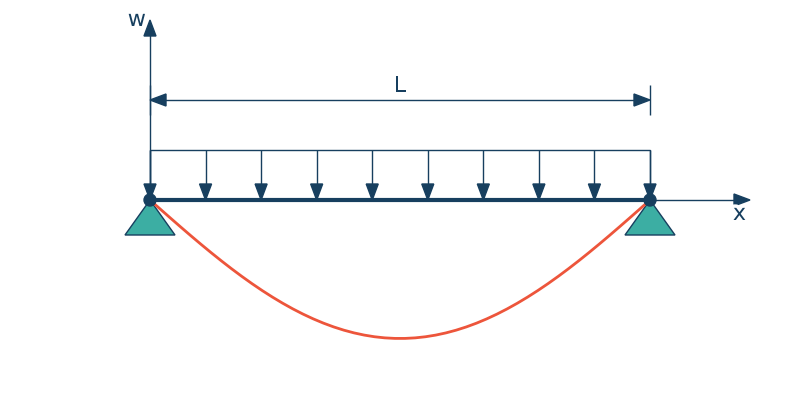
Równanie różniczkowe jest następujące

$$\cfrac{d^2w(x)}{dx^2} = -\cfrac{M(x)}{EI},\quad M(x) = -\frac{1}{2}qLx + \frac{1}{2}qx^2$$

z następującymi warunkami brzegowymi

$$w(0)= 0, \qquad w(L) = 0$$

Równanie zamieniamy na tożsamy układ równań różniczkowych pierwszego rzędu

$$dw/dx = \theta, \quad d\theta/dx = f$$ $$\cfrac{dw(x)}{dx} = \theta(x),$$ $$\cfrac{d\theta(x)}{dx} = -\cfrac{-\frac{1}{2}qLx + 0.5qx^2}{EI},$$

Aby rozwiązać dany układ równań musimy podać dwa warunki początkowe na ugięcie i kąt ugięcia. Ugięcie dla $x=0$ wynosi $0$. Nie znamy kąta obrotu na początku belki więc musimy coś założyć w pierwszym strzale. Metodą prób i błędów musimy tak dobrać początkowy kąt ugięcia aby ugięcie belki dla $x=L$ wynosiło $0$.