Metoda Eulera
Metody tego typu pozwalają nam na rozwiązywanie zagadnienia początkowego. Dane jest następujące równanie różniczkowe pierwszego rzędu (zagadnienie początkowe – Cauchy’ego)
$$\cfrac{dy}{dx} = f(x,y), \qquad y(x_0) = y_0$$Przybliżamy pochodną poprzez iloraz różnicowy dla pewnego parametru $h>0$:
$$\cfrac{y(x+h)-y(x)}{h}\approx \cfrac{dy}{dx}$$Zastępując pochodną w naszym równaniu ilorazem różnicowym otrzymujemy
$$\cfrac{y(x+h)-y(x)}{h} = f(x,y)$$Przekształcając powyższy wzór możemy zapisać
$$y(x+h) = y(x) + h f(x,y), \quad \text{lub}\quad y_{i+1} = y_i + h f(x_i,y_i)$$Otrzymaliśmy otwarty schemat Eulera. Dokładnie taki sam wzór dostaliśmy z rozwinięcia funkcji w szereg Taylora. Interpretacja graficzne wyprowadzonej metody jest następująca
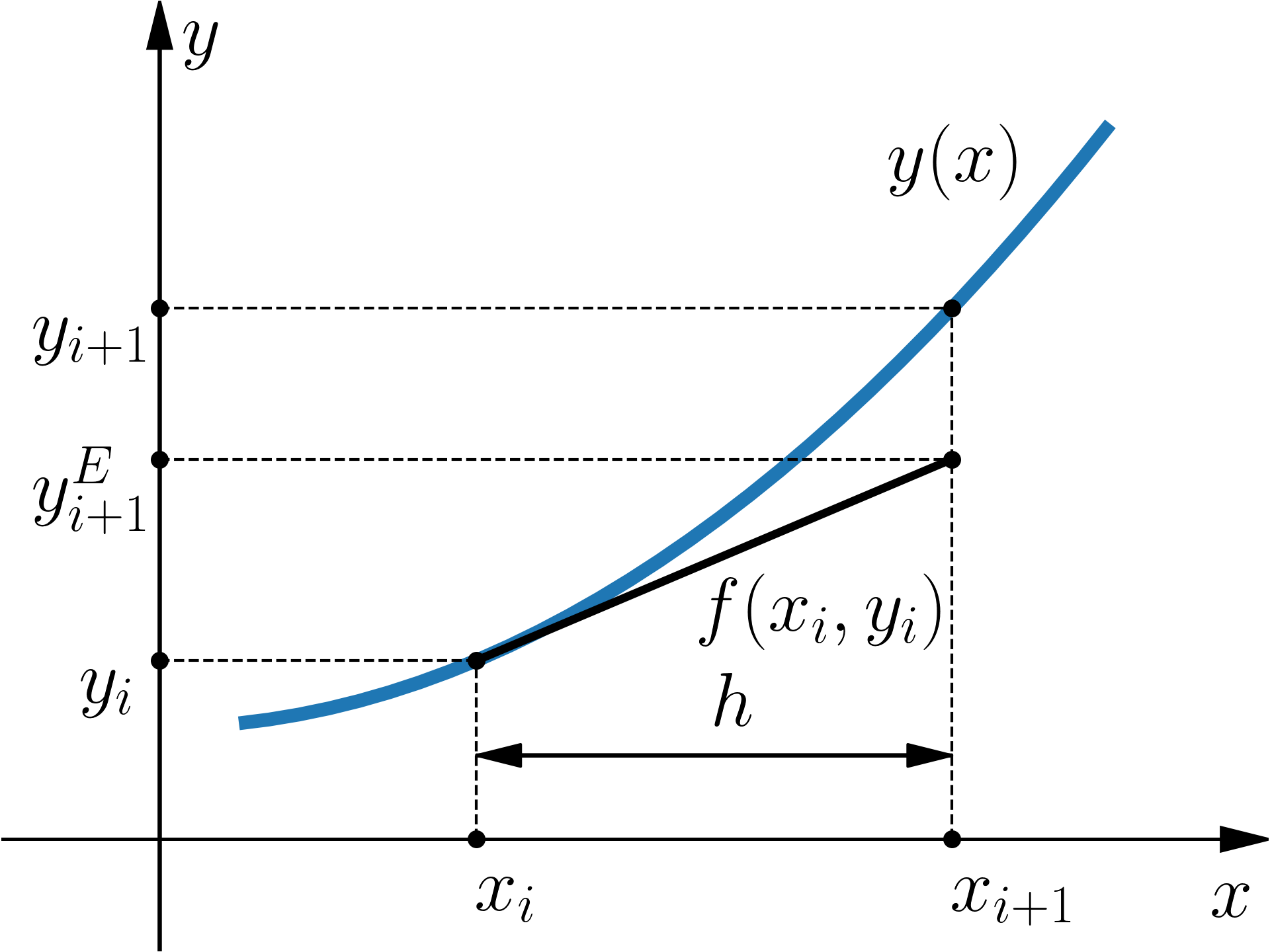
Rozwiąż następujący problem początkowy wykorzystując metodę Eulera.
$$\cfrac{dy}{dx} = f(x,y) = 1-xy, \text{warunek początkowy} \quad y(x=0)=1, \quad x \in \left<0, 3\right>$$Wykonajmy trzy pierwsze kroki tej metody przyjmując krok $h = 0.5$
$$y(0) = 1$$ $$y(0.5) = y(0) + h f(0, y(0)) = 1 + 0.5(1-0\cdot 1) = 1.5$$ $$y(1.0) = y(0.5) + h f(0.5, y(0.5)) = 1.5 + 0.5(1-0.5\cdot 1.5) = 1.625$$ $$y(1.5) = y(1.0) + h f(1.0, y(1.0)) = 1.625 + 0.5(1-1\cdot 1.625) = 1.3125$$Wyniki możemy zapisać w tabeli
| x | 0 | 0.5 | 1.0 | 1.5 |
|---|---|---|---|---|
| y | 1.0 | 1.5 | 1.625 | 1.3125 |
Otrzymaliśmy rozwiązanie dyskretne w postaci tabeli punktów (tablicowanie funkcji). Wartości między punktami możemy wyznaczyć korzystając z np. interpolacji liniowej.
Modyfikacje metody Eulera
Są różne warianty metody Eulera. Różnią się one między sobą sposobem wyznaczania wartości pochodnej.
Niejawna metoda Eulera
$$y_{i+1} = y_i + hf\left(x_{i+1},y_{i+1}\right)$$Równanie to jest w ogólności nieliniowe i musi być rozwiązane jedną z metod do rozwiązywania nieliniowego równania. Rząd błędu jest taki sam jak w zwykłej metodzie Eulera.
Metoda Eulera w tył (backward)
$$y_{i+1} = y_i + hf\left(x_{i+1},y_{i+1}^E\right) ,\qquad y_{i+1}^E = y_i + hf(x_i,y_i)$$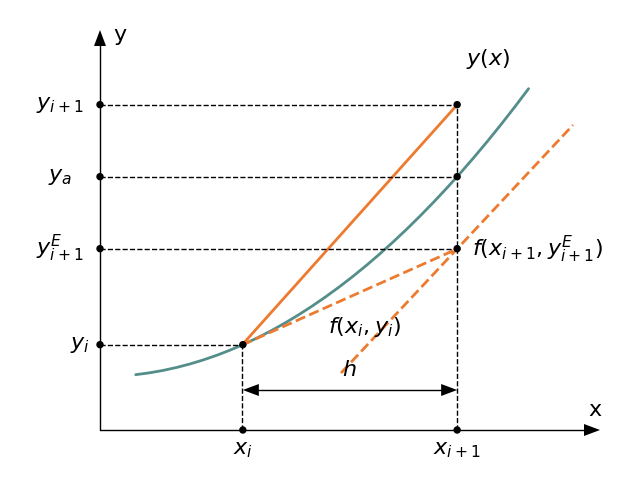
Zmodyfikowana metoda Eulera
$$y_{i+1} = y_i + h \cfrac{f(x_i,y_i) + f(x_{i+1},y_{i+1}^E)}{2},\qquad y_{i+1}^E = y_i + hf(x_i,y_i)$$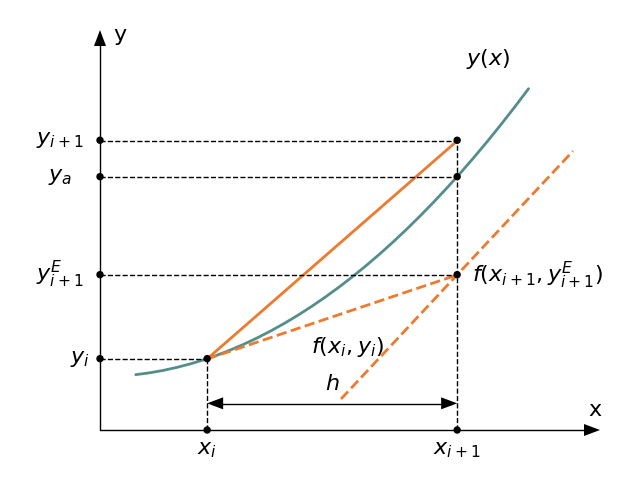
Metoda punktu środkowego (midpoint)
$$y_{i+1} = y_i + hf\left(x_i+\cfrac{1}{2}h,y_{i+\frac{1}{2}h}^E\right) ,\qquad y_{i+\frac{1}{2}h}^E = y_i + \cfrac{1}{2}hf(x_i,y_i)$$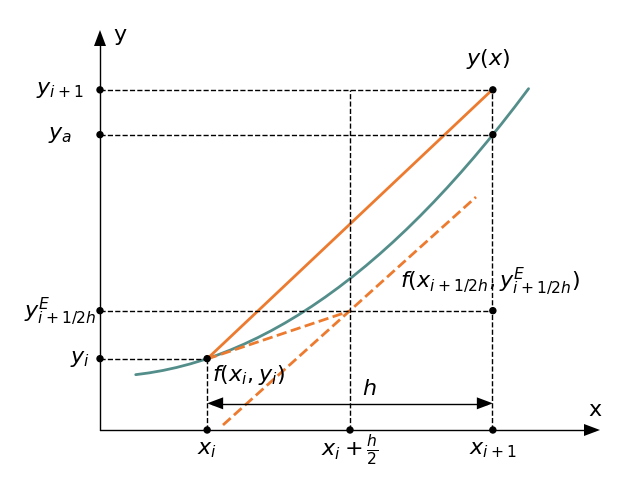
Błędy i stabilność rozwiązania
• błąd zaokrąglenia- wynika z założonej dokładności rozwiązania, może być istotny gdy krok $h$ jest mały. Błędy tego typu wynikają z arytmetyki zmiennoprzecinkowej w komputerze.
• błąd obcięcia - możemy podzielić na
- lokalny błąd obcięcia
- kumulowany błąd obcięcia.
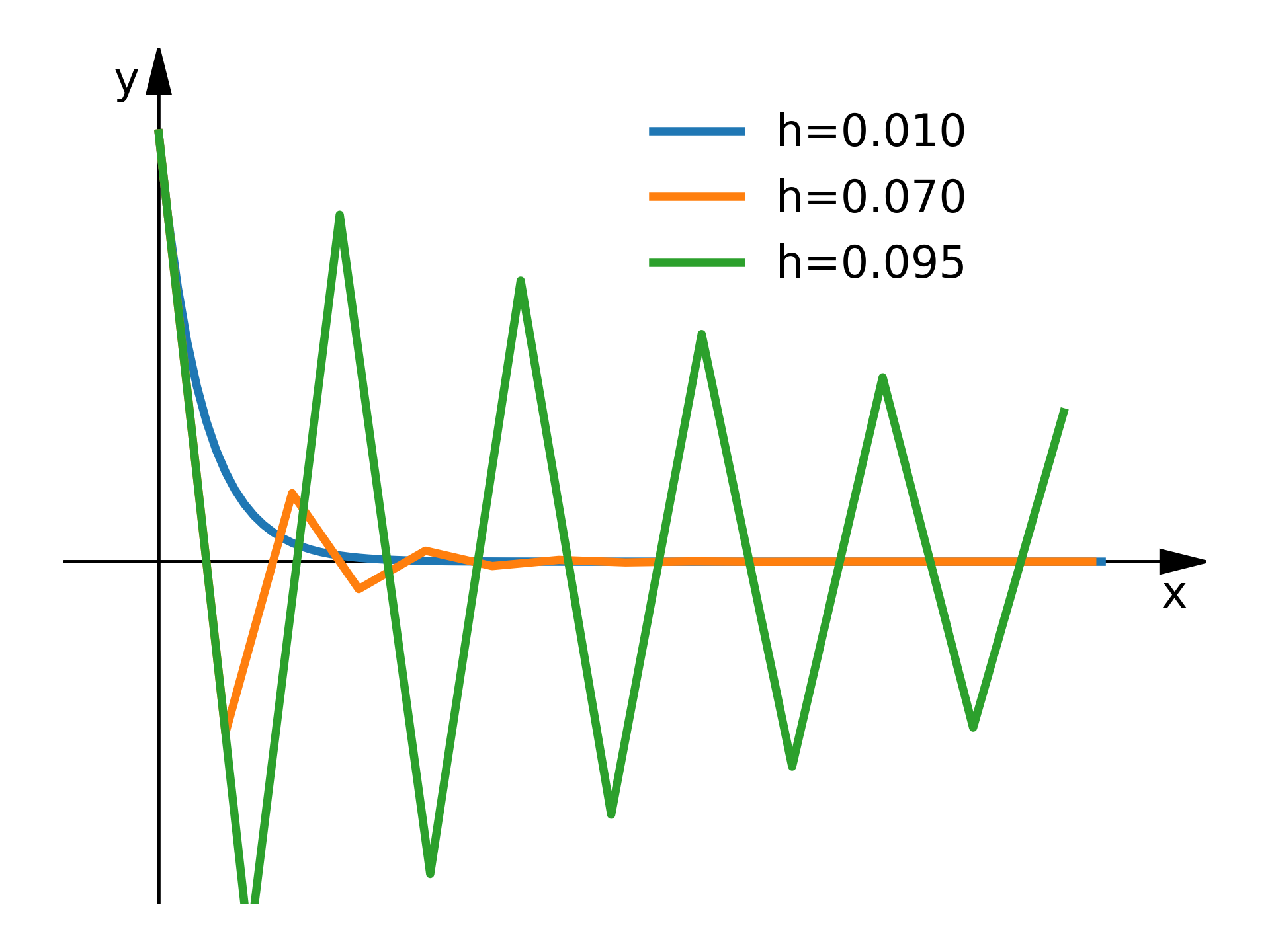
Wszystkie wymienione błędy dają razem całkowity błąd metody. Stabilność metody Eulera pokażmy na przykładzie równania różniczkowego pierwszego rzędu
Rozwiązaniem analitycznym tego równania jest funkcja $y = y_0e^{-ax}$. Rozważmy metodę Eulera w przód
$$y_{i+1} = y_{i} + (-ay_i)h, \qquad y_{i+1} = (1-ah)y_i$$Rozpisując dwa pierwsze kroki możemy zapisać
$$y_{1} = (1-ah)y_0, \quad y_{2} = (1-ah)y_1,$$Wstawiając $y_1$ do równania na $y_2$ dostajemy
$$\quad y_{2} = (1-ah)^2y_0,$$czyli ogólnie zapiszemy rozwiązanie na kroku $n$ jako
$$\quad y_{n} = (1-ah)^n y_0$$Ponieważ $a>0$ to dla kroku metody spełniającego nierówność
$$0 < h < 2/a, \quad |1-ah| < 1, \quad y_n \rightarrow 0, \quad n \rightarrow \infty$$Natomiast gdy krok metody Eulera jest
$$h>2/a, \quad |1-ah| > 1, \quad y_n \rightarrow \infty, \quad n \rightarrow \infty$$