Powtórka wiadomości

Pochodna, iloraz różnicowy

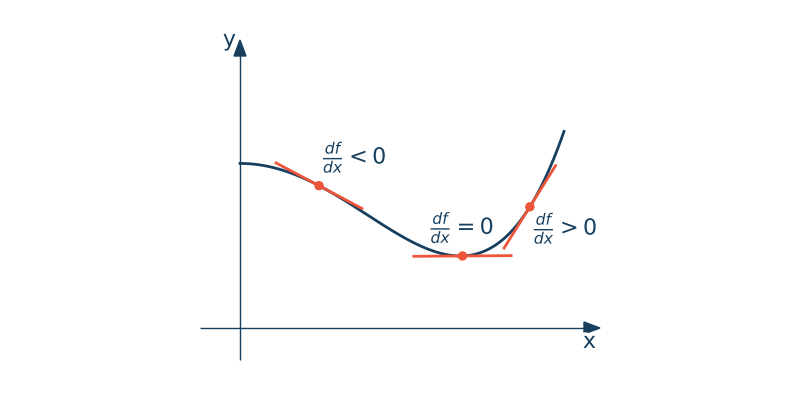
$$\cfrac{df}{dx} = f^{'}(x) = \lim_{h\rightarrow0}\cfrac{f(x+h)-f(x)}{h}$$

Różniczka to bardzo mała zmiana pewnej wielkości. Zapisujemy ją jako $dx$, gdzie $x$ jest pewną zmienną. Jeżeli zmiana jest mała (skończony przyrost) to często zapisujemy ją jako $\Delta x$ - przyrost zmiennej $x$.

Różniczkowanie

to operacja wyznaczania pochodnej funkcji. Pochodną po czasie funkcji $f$ często oznaczamy przez $\dot{f}$.

Szereg Taylora

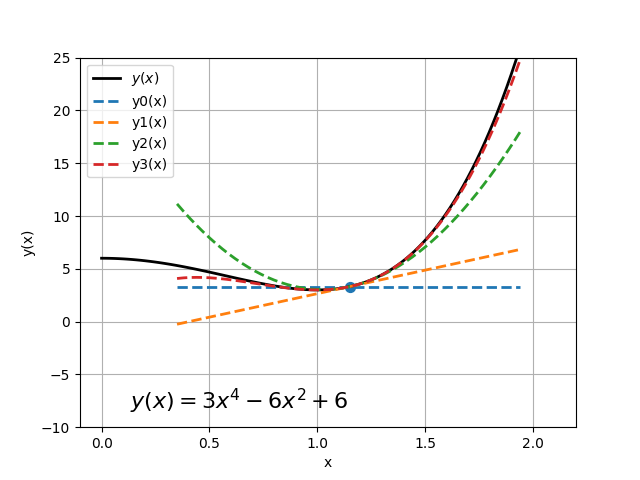
$$f(x+h) = f(x) + \cfrac{1}{1!}\cfrac{df(x)}{dx}h + \cfrac{1}{2!}\cfrac{d^2f(x)}{dx^2}h^2 + ...+\cfrac{1}{n!}\cfrac{d^nf(x)}{dx^n}h^n$$

Zostawiając tylko pierwsze dwa człony, otrzymujemy:

$$f(x+h) \approx f(x) + \cfrac{df(x)}{dx}h$$

Sprawdźmy jak wygląda przybliżenie funkcji $y(x)$ w zależności od liczby wyrazów szeregou Taylora oraz od wielkości kroku $h$ w otoczeniu punktu $x=1.2$. Widzimy, że dla dużych $h$, rozwiązanie nie jest dokładne. Ta sama zależność ma miejsce wraz ze zmniejszaniem się liczby wyrazów szeregu.

Równania różniczkowe zwyczajne

To takie równania w których występuję tylko jedna zmienna niezależna $x$. Najprostszą klasą równań różniczkowych są równania różniczkowe zwyczajne, (ang. ordinary differential equation - ODE), czyli równania postaci:

$$F\left(x,u, \cfrac{du}{dt}, \cfrac{d^2u}{dx^2}, ..., \cfrac{d^ku}{dx^k}\right) = F\left(x,u, u{'}, u{''}, ..., u^{k\times}{'}\right) = F(u)=0,$$

gdzie $u' = \dd{u}{x}$, $\quad u'' = \dd{^2u}{x^2}$ itd.

Problem: Znajdź funkcje $u(x)$ które spełniają powyższe równanie. Takie równanie różniczkowe zwyczajne nazywamy równaniem różniczkowym rzędu $k$. W praktyce (jak wyżej) zazwyczaj pomija się zapisywanie argumentu przy funkcji $u$ i jej pochodnych.

Problem początkowy

Zagadnieniem początkowe polega na znalezieniu funkcji, która spełnia dane równanie różniczkowe i warunek początkowy

$$\cfrac{du}{dx} = f(x,u), \qquad u(x_0) = u_0$$

W przypadku równania wyższego rzędu warunki początkowe muszą być również zadane na pochodne szukanej funkcji.

Problem brzegowy

Zagadnienie brzegowe – problem polegający na znalezieniu funkcji spełniającej dane równanie różniczkowe zdefiniowane w rozważanym obszarze wraz z warunkami brzegowymi które nałożone są na wartości funkcji i jej pochodne w więcej niż jednym punkcie tego obszaru.
warunki brzegowe typu Dirichleta i typu Neumanna
• warunek brzegowy Dirichleta (podstawowy) zadany na poszukiwaną funkcję np. podpory w konstrukcji
• Neumanna (naturalny) zadany na pochodną poszukiwanej funkcji np. obciążenia

Przykłady równań różniczkowych zwyczajnych (ODE)

Ugięcie belk wspornikowej

$$\cfrac{d^2w(x)}{dx^2} = -\cfrac{M(x)}{EI(x)}$$

gdzie $w$ - ugięcie belki, $M$ - moment zginający, $E$ - moduł Younga, $I$ - moment bezwładności przekroju belki

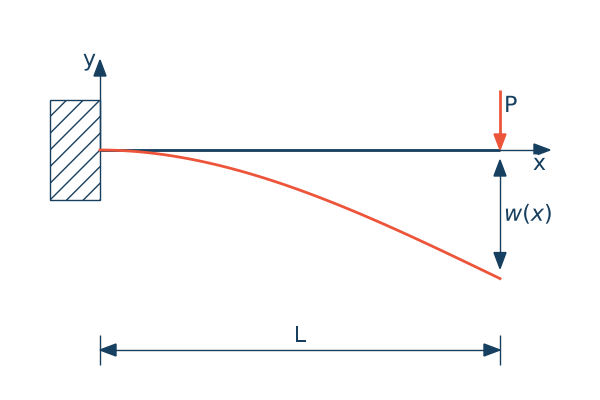
Zapiszmy równanie momentów zginających
$$M(x) = P(L-x)$$

oraz warunki początkowe czyli ugięcie i kąt obrotu w punkcie $x=0$ są równe zero
$$w(x=0) = 0, \quad \cfrac{dw}{dx}|_{x=0} = 0.$$

Równanie różniczkowe jest więc następujące:

$$\cfrac{d^2w(x)}{dx^2} = -\cfrac{ P(L-x)}{EI}$$

Rozwiązanie analityczne jest następujące

$$w(x) = \cfrac{P}{6EI}x^3- \cfrac{PL}{2EI}x^2$$

Jednoosiowe rozciąganie pręta

$$EA\cfrac{d^2u(x)}{dx^2} + q = 0$$

Wyznaczenie przemieszczenia i siły w pręcie jako przykład zagadnienia brzegowego

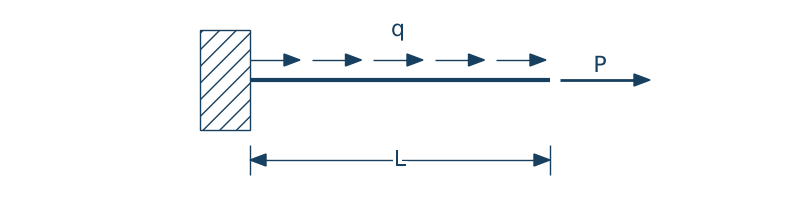
Warunki brzegowe są następujące

$$u(x=0) = 0, \qquad N(x=L) = EA\left. \cfrac{du}{dx}\right|_{x=L} = P$$

Nasze rozwiązanie ma następująca postać
$$u(x) = \cfrac{1}{EA} \left[-\cfrac{1}{2}qx^2 + \left(P + qL\right)x\right]$$

Różniczkują powyższe równanie dostajemy funkcję odkształcenia
$$\varepsilon = \cfrac{1}{EA} \left(-qx + P + qL \right)$$

oraz przemnażając wynik przez $EA$ dostajemy funkcje siły w pręcie
$$\qquad N(x)= -qx + P + qL$$

Równanie różniczkowe cząstkowe

(PDE) Partial differential equation - pochodne występujące w równaniu różniczkowym są obliczane względem wielu zmiennych np. względem przestrzeni ($x_1,x_2, x_3)$ i czasu ($t$). Przykłady równań różniczkowych cząstkowych:
• nieustalony przepływ ciepła, paraboliczne równanie różniczkowe nieustalonego przewodzenia ciepła zwane jest równaniem Fouriera-Kirchhoffa w przypadku 2d $T(t, x_1, x_2)$

$$\rho c \pp{T}{t} = k\Delta T + q, \qquad \Delta T = \pp{^2T}{x_1^2} + \pp{^2T}{x_2^2} + \pp{^2T}{x_3^2}$$

gdzie $\rho$ -gęstość materiału, $c$ - ciepło właściwe, $k$ - współczynnik przewodzenia ciepła, $q$ - wewnętrzne źródła ciepła. Równanie to zakłada że nie ma anizotropii materiału ze względu na przewodzenie i dlatego używamy skalarnego współczynnika przewodzenia ciepła $k$.

• równanie falowe

$$\pp{^2 u}{t^2} - \Delta u= f, \qquad\Delta u = \pp{^2 u}{x_1^2} + \pp{^2 u}{x_2^2} +\pp{^2 u}{x_3^2}$$

• płyty cienkie Kirchhoffa-Love'a - stan giętny

$$\pp{^4 w(x_1,x_2)}{x_1^4} + 2\pp{^4 w(x_1,x_2)}{x_1^2 \partial x_2^2} + \pp{^4 w(x_1,x_2)}{x_2^4} = \cfrac{q}{D}, \quad D = \cfrac{Eh^3}{12(1-\nu^2)},$$

gdzie: $h$ - grubość płyty, $E$ - moduł Younga, $\nu$ - współczynnik Poissona, $q$ - obciążenie, $w(x_1, x_2)$ - funkcja ugięcia płyty.