Komputerowe Wspomaganie Projektowania

Dwuwymiarowy przepływ ciepła

exec('assem.sci'); 
exec('coordxtr.sci');
exec('eldraw2.sci');
exec('extract.sci');
exec('solveq.sci'); 
exec('flw2qs.sci'); 
exec('statcon.sci'); 
exec('flw2qe.sci');
exec('flw2te.sci');
exec('flw2ts.sci');
exec('elflux2.sci');
exec('eliso2.sci');

Rozważmy bardzo proste zagadnie przypływu ciepła w dwóch wymiarach. Lewa krawędź tarczy ma ustalona temperatur $T=0$, natomiast prawa krawędź ma zaday strumień ciepła $q$.

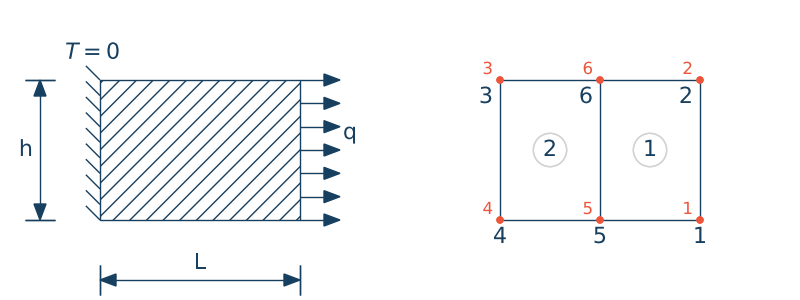
• definicja współrzędnych węzłów ramy $\mathbf{nodes}$
• definicja elementów $\mathbf{elements}$

Element flw2qe składa się z 4 węzłów. W każdym węźle mamy jeden stopniń swobodny związany z temperaturą.

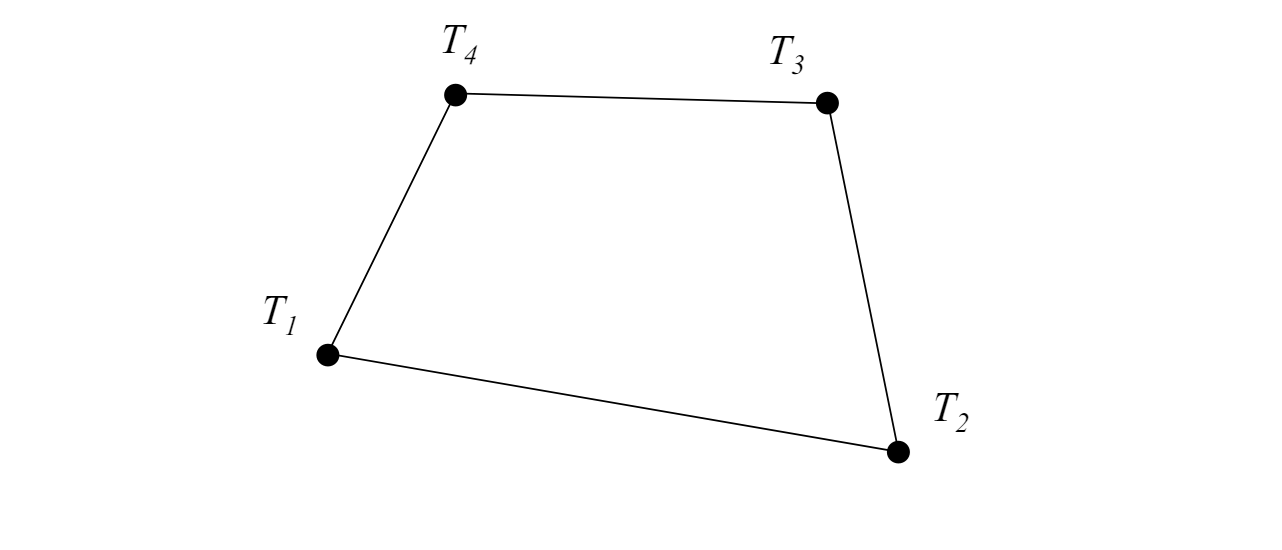
Czterowęzłowy element skończony o jednym stopniu swobody w każdym wężle.

Macierz stopni swobody

for i=1:LE
    n1 = elements(i,1)
    n2 = elements(i,2)
    n3 = elements(i,3)
    n4 = elements(i,4)
    Ex(i,:) = [nodes(n1,1),nodes(n2,1),nodes(n3,1),nodes(n4,1)];
    Ey(i,:) = [nodes(n1,2),nodes(n2,2),nodes(n3,2),nodes(n4,2)];
    Edof(i,:)=[i, n1, n2, n3, n4];
end

Tensor przewodności cieplnej

W ogólnym przypadku tensor przewodności cieplnej jest następujący

$$\mathbf{D} = \begin{bmatrix} k_{xx} & k_{xy} \\ k_{yx} & k_{yy} \end{bmatrix}, \quad \mathbf{D}^{iso} = \begin{bmatrix} k & 0 \\ 0 & k \end{bmatrix}$$

Prawo konstytutywne przepływu ciepła - liniowa zależność między strumieniem ciepła $\mathbf{q}$ a gradientem temperatury $ \nabla T$.

$$\mathbf{q} = -\mathbf{D} \nabla T$$

//ep - grubość elementu
ep=1; 
D=[1 0;0 1];

# Przykład

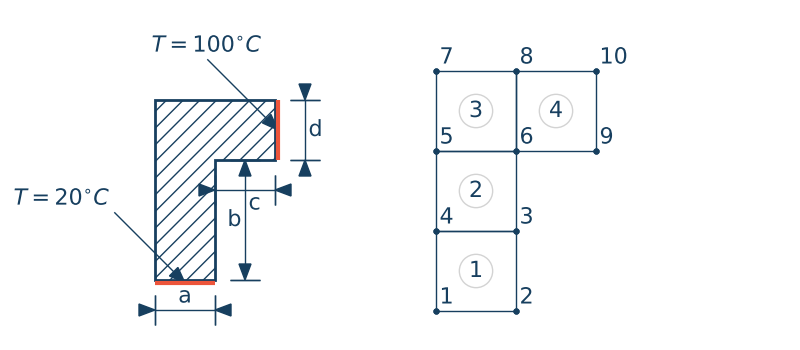
Wyznacz rozkład temperatury. Przyjmij następujące parametry:
• $a = 2m$
• $b = 4m$
• $c = 2m$
• $d = 2m$
• współczynnik przewodzenia ciepła $k=0.6$
• grubość tarczy $t= 0.1$