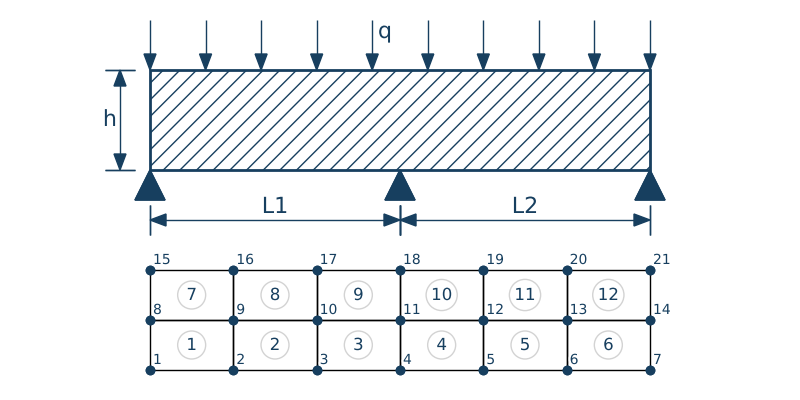
Tarcza - płaski stan naprężenia
Ładowanie wykorzystywanych funkcji bibliotecznych
exec('eldraw2.sci');
exec('eldisp2.sci');
exec('coordxtr.sci');
exec('solveq.sci');
exec('hooke.sci');
exec('plani4e.sci');
exec('assem.sci');
exec('extract.sci');
exec('plani4f.sci');
exec('plani4s.sci');
Rozważmy bardzo prostą tarczę w kształcie prostokąta o wymiarach $L\times h$. Tarcza ma grubość $t$ i jest obciążona na górnej powierzchni obciążeniem ciągłym $q$. Dwa dolne wierzchołki są podparte zgodnie z rysunkiem.
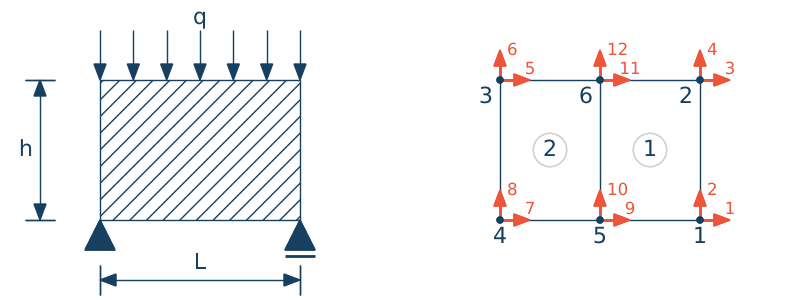
• definicja współrzędnych węzłów ramy $\mathbf{nodes}$
• definicja elementów $\mathbf{elements}$
• definicja własności elementu skończonego $\mathbf{ep}$:
ep = [1 t 3]
W wektorze ep pierwsza składowa oznacza typ analizy (1- płaski stan naprężenia), druga składowa $t$ to grubość tarczy natomiast ostatnia składowa oznacz regułę całkowania, w tym wypadku całkowanie z użyciem 3 punktów Gaussa.
Element tarczy plani4e składa się z 4 węzłów. W każdym węźle mamy dwa stopnie swobodny. W sumie rozważany element skończony posiada 8 stopni swobody.
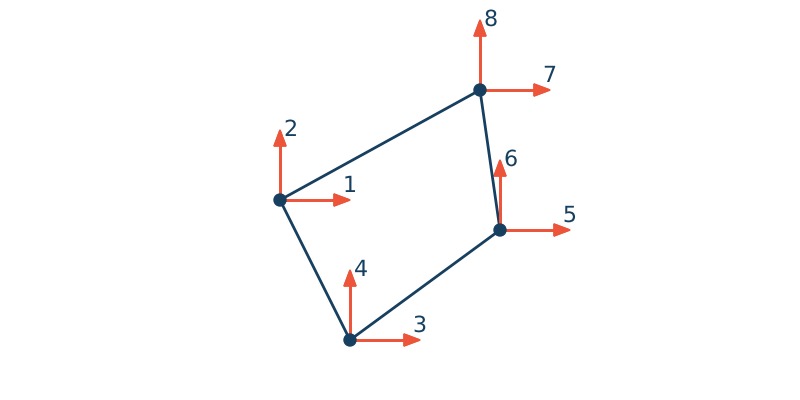
Równanie konstytutywne (fizyczne)
Do zdefiniowania równania fizycznego posługujemy się funkcją hooke, która przyjmuje trzy parametry: typ analizy zdefiniowany jako pierwsza składowa wektora ep, Moduł Younga E i współczynnik Poissona v.
E=210000;
v=0.3;
t=1;
ep=[1 t 3];
D=hooke(ep(1),E,v)
Powyższa funkcja generuje macierz D która dla rozważanego przypadku tarczy o materiale linio-sprężystym jest następująca
Macierz stopni swobody Edof oraz macierze zawierające wspórzędne danych elementów ( Ex Ey ) generujemy za pomocą następującej pętli
for i=1:LE
n1 = elements(i,1)
n2 = elements(i,2)
n3 = elements(i,3)
n4 = elements(i,4)
Ex(i,:) = [nodes(n1,1),nodes(n2,1),nodes(n3,1),nodes(n4,1)]
Ey(i,:) = [nodes(n1,2),nodes(n2,2),nodes(n3,2),nodes(n4,2)]
Edof(i,:)=[i,2*n1-1,2*n1, 2*n2-1,2*n2,2*n3-1,2*n3,2*n4-1,2*n4]
end
Pętla wykonywana jest po wszystkich elementach skończonych, a wiec LE oznacza liczbę wszystkich elementów.
# Przykład
• Moduł Younga $E = 210000$Pa,
• współczynnik Poissona $\nu=0.3$.
• Grubość tarczy jest równa $0.2$m. Obciążenie ciągłe $q$ jest równe $5kN$.
• a = 0.6m
• b = 3m
• h = 4m
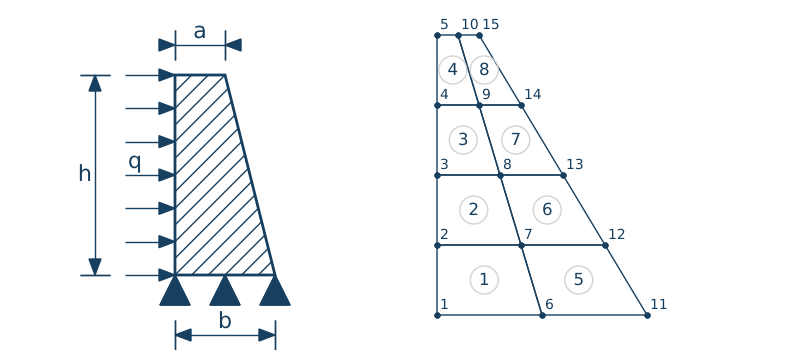
# Przykład
• Moduł Younga $E = 35$GPa,
• współczynnik Poissona $\nu=0.32$.
• Grubość tarczy jest równa $0.35$m. Obciążenie ciągłe $q$ jest równe $3kN$.
• h = 0.8m
• L1 = 2.5m
• L2 = 2.5m