CALFEM - wprowadzenie

CALFEM czyli Computer Aided Learning the Finite Element Method

Program do wspomagania nauczania Metody Elementów Skończonych. Program zawiera szereg procedur pozwalających na:
• budowanie macierzy sztywności elementu
• agregację globalnej macierzy sztywności
• rozwiązywanie układu równań
• obliczanie sił, naprężeń i odkształceń
• wizualizację wyników (konfiguracja początkowa i zdeformowana, wykresy sił przekrojowych)

Instalacja:
• ściągamy i rozpakowujemy pliki programu
• ustawiamy aktualny katalog roboczy na folder zawierający pliki programu

Kratownica - CALFEM

• każdy pręt traktujemy jako jeden element skończony
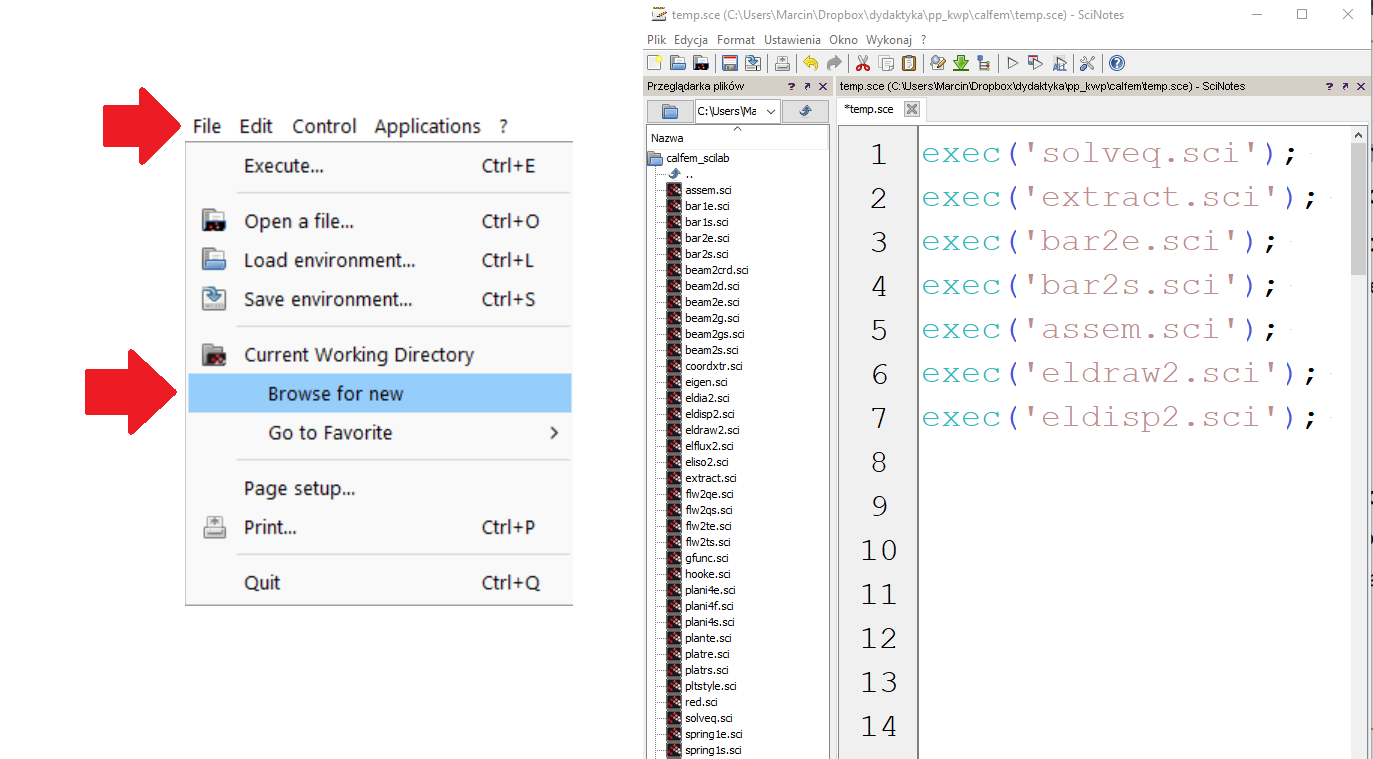
• Ładowanie potrzebnych funkcji

exec('solveq.sci'); 
exec('extract.sci'); 
exec('bar2e.sci'); 
exec('bar2s.sci'); 
exec('assem.sci'); 
exec('eldraw2.sci'); 
exec('eldisp2.sci');

Rozważmy bardzo prostą kratownicę jak na rysunku

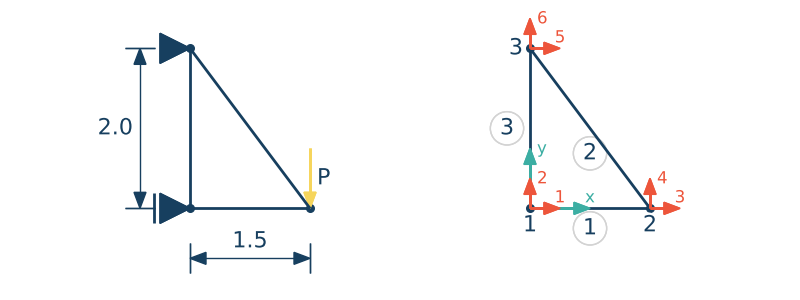
Aby wyznaczyć przemieszczenia kratownicy musimy wykonać następujące kroki:

• definicja współrzędnych węzłów kratownicy $\mathbf{nodes}$. Jest to macierz o wymiarach $N \times 2$ gdzie $N$ oznacza liczbę węzłów kratownicy. Pierwsza kolumna zawiera współrzędne $x$ węzłów, druga kolumna zawiera współrzędne $y$ w przyjętym układzie współrzędnych.

nodes=[0.0 0.0; 1.5 0.0; 0.0 2.0]

• definicja prętów kratownicy $\mathbf{elements}$ (elementów). Macierz ta ma wymiary $M\times 2$ gdzie $M$ oznacza liczbę prętów z których składa się rozważana kratownica. Kolejne wierszy macierzy zawierają indeksy węzłów z których składa się kolejny pręt. Każdy pręt składa się z dwóch węzłów dlatego liczba kolumn tej macierzy wynosi 2. Kolejność wpisywania indeksów węzłów nie ma znaczenia to znaczy nie ma znaczenia który węzeł uznamy jako początkowy a który jako końcowy.

elements = [1 2; 2 3; 3 1]

• definicja własności elementu skończonego $\mathbf{ep}$, to wektor o dwóch składowych: moduł Younga $E$ i pole przekroju poprzecznego pręta $A$

ep = [E A]

• do narysowania kratownicy służy funkcja eldraw2. Wywołanie tej funkcji jest następujące:

eldraw2(Ex,Ey,Elnum);

Funkcja przyjmuje trzy argumenty które oznaczają kolejno
• macierz zawierającą współrzędne x węzłów z których składają się dany element
• macierz zawierającą współrzędne y węzłów z których składają się poszczególne elementy
• wektor zawierający numery elementów

# Zadanie

Oblicz współrzędne wektora przemieszczenia węzłów dla kratownicy jak na rysunku. Narysuj postać kratownicy w konfiguracji początkowej i zdeformowanej.

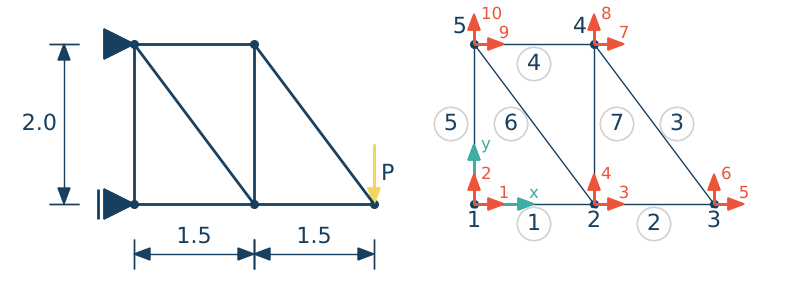
Każdy pręt kratownicy wykonany jest z tego samego materiału o module Younga $E=120 GPa$ oraz ma taki sam przekrój poprzeczny o polu $A = 0.03 m^2$

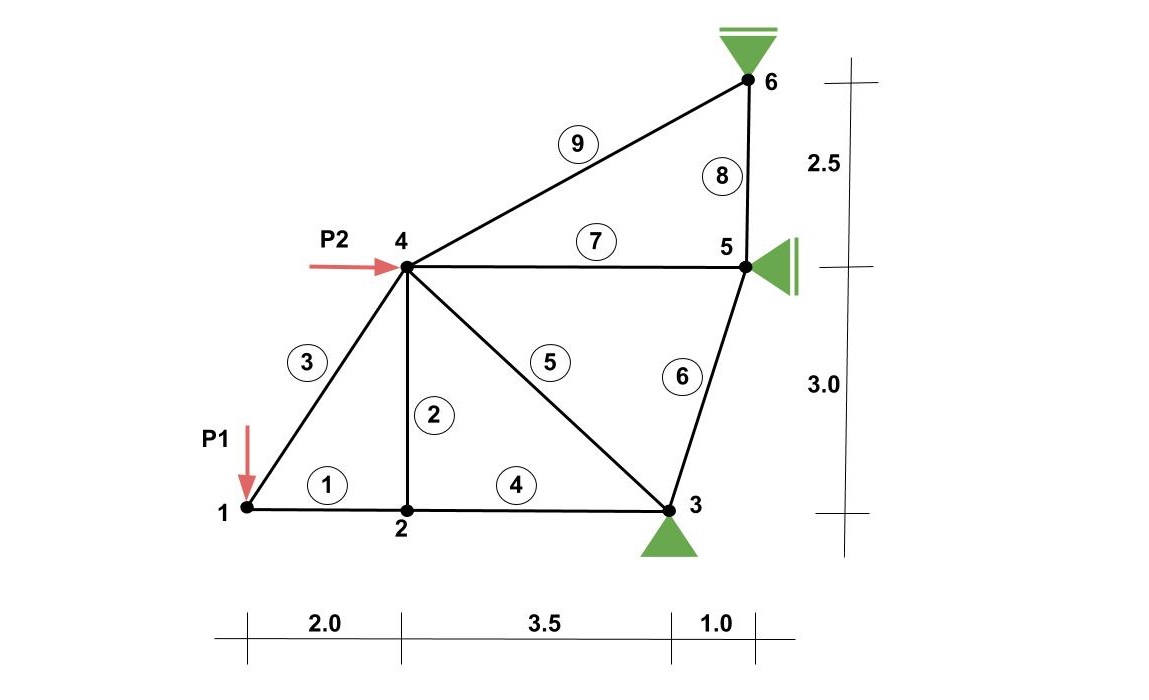
# Zadanie

Oblicz siły w prętach dla kratownicy ja na rysunku. Narysuj wykres zdeformowanej kratownicy pod wpływem przyłożonych obciążeń.

Różne warianty zadań
• siła skupiona nachylona pod kątem
• osiadanie podpory
• zmienna sztywność (przekrój, moduł Younga)

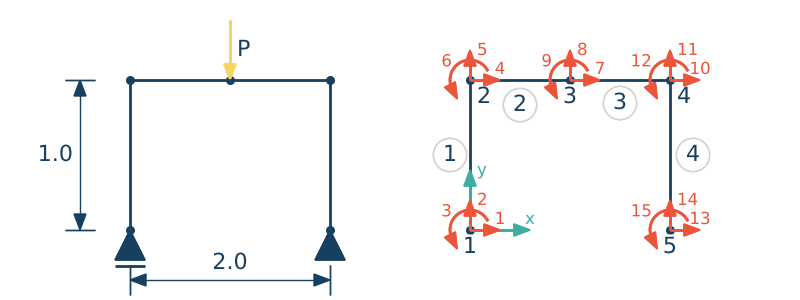
Rama - CALFEM

• o podziale na elementy skończone decyduje geometria ramy, położenie podpór i obciążenia
• Ładowanie potrzebnych funkcji

exec('solveq.sci'); 
exec('extract.sci'); 
exec('coordxtr.sci');
exec('beam2e.sci'); 
exec('beam2s.sci'); 
exec('assem.sci'); 
exec('eldraw2.sci'); 
exec('eldisp2.sci'); 
exec('beam2crd.sci');