Wprowadzenie
W pakiecie Scilab (matematyczne narzędzie w języku Scilab) funkcja int2d jest używana do obliczania całek podwójnych numerycznie. Funkcja ta stosuje metodę przybliżenia obszaru całkowania do siatki punktów, a następnie sumuje wartości funkcji na tej siatce w celu uzyskania przybliżonej wartości całki.
Dla obszaru prostokątnego wywołanie funkcji jest następujące
[I, err] = int2d(xmin, xmax, ymin, ymax, f)
gdzie xmin, xmax, ymin, ymax oznaczają granice całowania względem zmiennej $x$ i $y$, f - to nazwa funkcji którą chcemy całkować
# Przykład
Oblicz następując całkę
$$I = \int_0^1 \int_1^2 \cfrac12xy dydx$$function z = fun(x,y)
z = 0.5*x*y
endfunction
//
[I,e] = int2d(0,1,1,2,fun)
disp(I)
W przypadku nieregularnego obszaru wywołanie funkcji jest następujące
[I, err] = int2d(X, Y, f)
w tym przypadku X i Y są macierzami o wymiarach $3\times n$ zawierającymi współrzędne wierzchołków trójkątów które tworzą nieregularny obszar. Zmienna $n$ oznacza liczbę takich trójkątów.
Dla przykładu macierze $\X$ i $\Y$ dla przestawione na rysunku przykładu podziału obszaru na dwa trójkąty są następujące
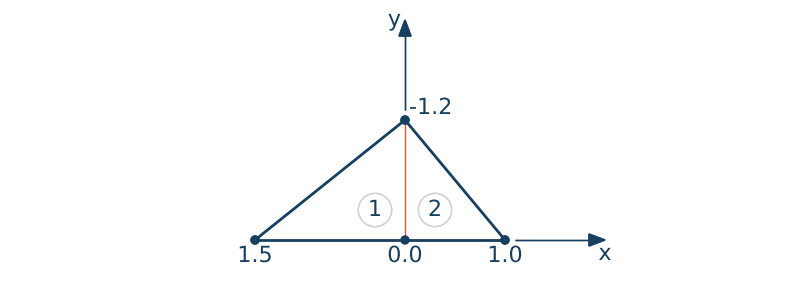
Numery trójkątów oznaczone są cyfrą w kołku. wspórzędne wierzchołkow pierwszego trójką zanodują sie w pierwsze kolumnie macierzy $\X$ oraz $\Y$. Analogicznie dla trójkąta drugiego będzie to druga kolumna. Macierz $X$ zawiera wspórzedne $x$ każdego z wierzchołów a mcierzy $\Y$ zawiera współrzędne $y$. Nie ma znaczenie od którego wierzchołka trójkąta zaczniemy.
$$\X = \begin{bmatrix}0.0 & 0.0 \\ 0.0 & 1.0 \\ 1.5 & 0.0\\ \end{bmatrix} ,\qquad \Y = \begin{bmatrix} 0.0 & 0.0 \\ 1.2 & 0.0 \\ 0.0 & 1.2\\ \end{bmatrix}$$# Przykład
Oblicz następując całkę wykorzystując podział obszaru na jeden trójkąt.
$$I = \int_0^1 \int_0^{-x+1} \cos(x+y) dydx$$function z = fun(x,y)
z = cos(x+y)
endfunction
X = [0 1 0]';
Y = [0 0 1]';
[I,e] = int2d(X,Y,fun)
disp(I)