Funkcja rand

Funkcja rand w Scilab służy do generowania liczb losowych. Może generować liczby w różnych rozkładach, a także tworzyć macierze liczb losowych o zadanych wymiarach.

Składnia

• rand() – generuje jedną liczbę losową.

• rand(m, n) – generuje macierz $ m \times n $ liczb losowych.

• rand(m, n, 'uniform') – generuje macierz $ m \times n $ z liczbami o równomiernym rozkładzie.

• rand(m, n, 'normal) – generuje macierz $ m \times n $ z liczbami o rozkładzie normalnym (średnia $ 0 $, odchylenie standardowe $1$.

• rand('seed', value) – ustawia ziarno generatora liczb losowych.

Przykłady wykorzystania

• Generowanie pojedynczej liczby losowej:

num = rand()
disp(num)

Generowanie macierzy $3\times 3$ liczb losowych:

A = rand(3, 3)
disp(A)

• Generowanie macierzy z liczbami o rozkładzie normalnym:}

B = rand(2, 5, 'normal)

Ustawienie ziarna i generowanie powtarzalnych wyników:

rand('seed', 12345)
C = rand(2, 2)}
disp(C)

Losowe próbkowanie z danych:

data = [1, 2, 3, 4, 5]
sample = data(ceil(rand(1, 3) * size(data, 'r')))
disp(sample)

Do graficznej reprezentacja rozkładu danych używany jest histogram który pozwala zrozumieć, jak często występują różne wartości w zbiorze danych. Jest to rodzaj wykresu kolumnowego, w którym oś pozioma (oś X) reprezentuje przedziały wartości danych (zwane binami), a oś pionowa (oś Y) pokazuje liczebność danych w tych przedziałach. W Scilab istnieje specjalna funkcja która pozwala rysować histogram

histplot(n, data)

gdzie n to całkowita liczba dodatnia reprezentująca liczbę przedziałów histogramu, data - wektor zawierający dane.

# Przykład

Wygeneruj 1000 licz losowych o rozkładzie normalnym oraz przedstaw otrzymany zbiór danych w postaci histogramu.

// Ustawienie ziarna generatora liczb losowych dla powtarzalności wyników
rand("seed", 0);
// Generowanie wektora 1000 liczb losowych o rozkładzie normalnym
data = rand(1, 1000, "normal");
// Określenie liczby przedziałów histogramu
num_bins = 20;
histplot(num_bins, data);
xtitle("Histogram rozkładu normalnego")
xgrid();

# Przykład

Utwórz macierz $5 \times 5$ wypełnioną losowymi liczbami z przedziału $[0, 1]$ Następnie:
• Oblicz średnią oraz odchylenie standardowe wszystkich elementów macierzy.
• Znajdź minimalną i maksymalną wartość w macierzy.

# Przykład

Używając funkcji rand , zasymuluj 100 rzutów monetą:

• Zapisz wyniki w wektorze, przyjmując $ 0 $ dla reszki i $ 1 $ dla orła.
• Policz, ile razy wypadł orzeł, a ile razy reszka.
• Zwizualizuj wyniki za pomocą histogramu.

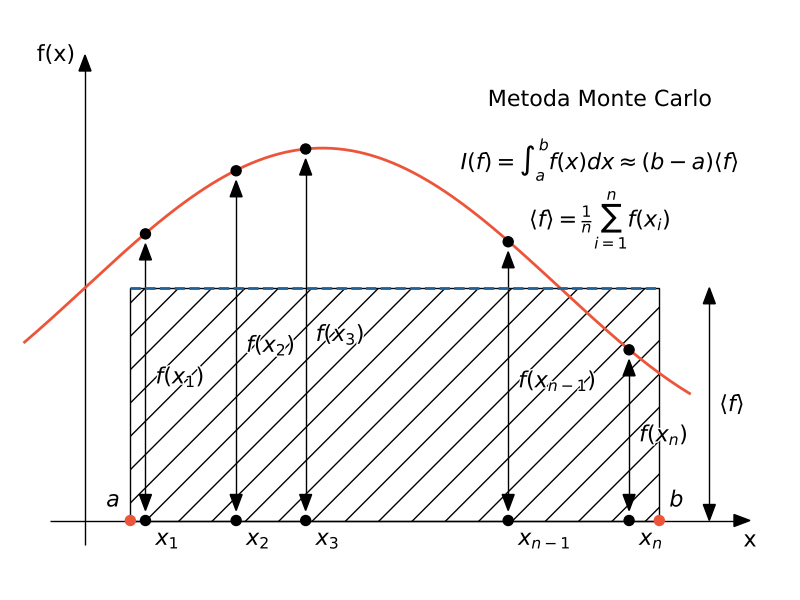
Metoda Monte Carlo

Metoda ta polega losowaniu próbek z przestrzeni, którą chcemy całkować. Jest ona szczególnie użyteczna do całkowania funkcji w wielowymiarowych przestrzeniach.

Ogólny algorytm metody Monte Carlo do całkowania funkcji $f(x)$ w przedziale $[a, b]$ jest następujący

Określ obszar całkowania
Określ przedział całkowania $[a, b]$ dla każdej zmiennej niezależnej.

Generuj losowe punkty
Wygeneruj losowe punkty $x_i$ wewnątrz obszaru całkowania. Liczba punktów do wygenerowania zależy od wymaganej precyzji

Oblicz wartość funkcji dla każdego punktu
Oblicz wartość funkcji $f(x_i)$ dla każdego wygenerowanego punktu $x_i$

Oblicz średnią wartość funkcji
Oblicz średnią wartość funkcji na podstawie wszystkich wygenerowanych punktów:

gdzie $N$ to liczba wygenerowanych punktów.

Oblicz przybliżoną wartość całki
Przybliżoną wartość całki możesz uzyskać, mnożąc średnią wartość funkcji przez objętość obszaru całkowania:

gdzie $V$ to objętość obszaru całkowania.

Interpretacja graficzna przybliżenia całki oznaczonej metodą Monte Carlo.

# Przykład

Opracuj program który oblicza wartość całki oznaczonej dla funkcji $f(x)$ na przedziale $[a,b]$ wykorzystując metodę Monte Carlo. Przyjmij liczbę punktów $n=10000$

Obliczoną wartość całki porównaj z wartością dokładną.

Całkowanie funkcji dwóch zmiennych

Metoda Monte Carlo pozwala na przybliżone obliczenie wartości całki podwójnej funkcji dwóch zmiennych. Rozważmy funkcję $ f(x, y) $, którą chcemy scałkować na prostokątnym obszarze $ D = [a, b] \times [c, d] $. Całka podwójna przyjmuje postać:

W celu przybliżenia tej całki za pomocą metody Monte Carlo wykonujemy następujące kroki:

• Określamy obszar całkowania $ D = [a, b] \times [c, d] $. Powierzchnia tego obszaru wynosi:

• Generujemy $ N $ punktów $ (x_i, y_i) $ losowo i równomiernie w obszarze $ D $. Punkty $ x_i $ oraz $ y_i$ są generowane przy użyciu funkcji rand

• Obliczamy wartości funkcji \( f(x_i, y_i) \) dla każdego z wylosowanych punktów.

• Wyznaczamy średnią wartość funkcji na podstawie wszystkich próbek:

• Przybliżenie wartości całki wynosi:

# Przykład

Opracuj program który oblicza wartość całki oznaczonej dla funkcji $f(x,y)$ na przedziale $x\in[-3,0]$, $y\in[-2,2]$ wykorzystując metodę Monte Carlo. Przyjmij liczbę punktów $n=10000$