Wprowadzenie
Całkowanie numeryczne to technika przybliżonego obliczania wartości całki danej funkcji matematycznej. Istnieje kilka różnych metod całkowania numerycznego, z których niektóre są bardziej efektywne dla określonych rodzajów funkcji lub problemów.
Popularne metody całkowania numerycznego
Metoda prostokątów
Ta metoda polega na podziale obszaru pod krzywą na prostokąty i obliczaniu sumy pól tych prostokątów.
Metoda trapezów
Podobna do metody prostokątów, ale zamiast prostokątów używane są trapezy.
Metoda Simpsona
Ta metoda wykorzystuje wielomiany drugiego stopnia (parabolę) do przybliżania krzywizny funkcji. Działa dobrze dla funkcji, które są "podobne" do parabol.
Metoda Gaussa
Jest to rodzina algorytmów, które wykorzystują węzły Gaussa do dokładniejszego przybliżenia wartości całki.
Metoda Monte Carlo
Ta metoda opiera się na losowaniu punktów w obszarze pod krzywą i używaniu proporcji punktów znajdujących się pod krzywą do całości obszaru, aby obliczyć całkę.
Scialba posiada wbudowane funkcje do obliczania całek oznaczonych. Do całowania metodą trapezów służy funkcja inttrap(x,s), która przyjmuje dwa parametry. Wektor x zawiera wzrastające współrzędne dla przedziału całkowania, natomiast wektor s wartości funkcji odpowiadające współrzędnym zawartym w wektorze x.
# Przykład
Oblicz wartość całki oznaczonej dla funkcji $f(x)=2x$ na przedziale [0,2] wykorzystując funkcję inttrap.
function y=fun(x)
y = 2*x
endfunction
x= 0:0.2:2
y = fun(x)
w = inttrap(x,y)
disp(w)
# Przykład
Oblicz wartość całki oznaczonej.
$$\int_{-\pi}^{\pi} 2sin(3x)dx$$# Przykład
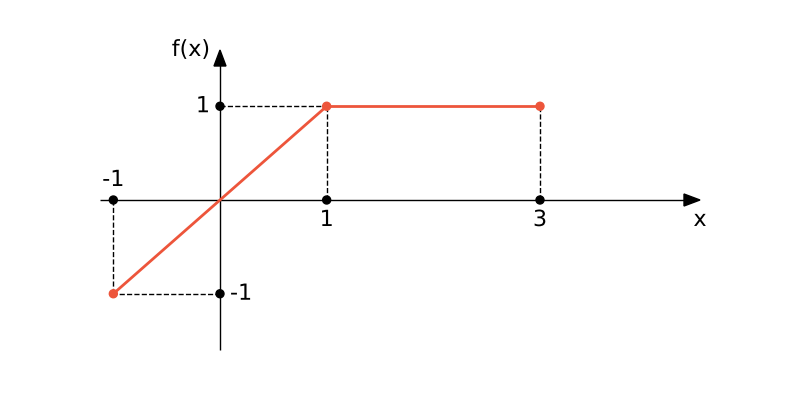
Oblicz wartość całki oznaczonej dla funkcji $f(x)$ jak na rysunku w przedziale $[-1,3]$ wykorzystując funkcję inttrap. Do zdefiniowaniu funkcji $f(x)$ użyj pętli for oraz konstrukcji warunkowej if else.
Metoda prostokątów
Metoda prostokątów to jedna z najprostszych technik całkowania numerycznego. Istnieją różne warianty tej metody, takie jak metoda prostokątów lewych, prawych i środkowych.
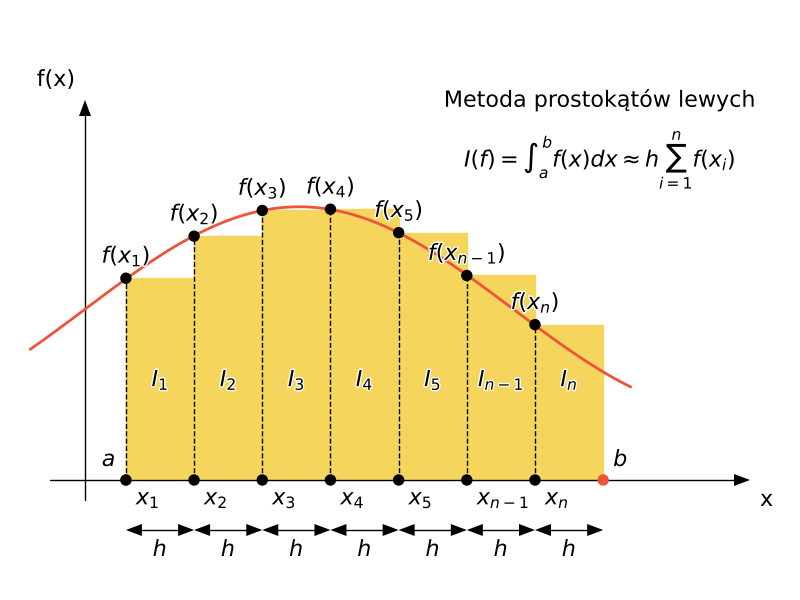
Wartość całki oznaczonej jest przybliżana sumą prostokątów według poniższego wzoru.
$$I(f) = \int_a^b f(x) dx \approx h \sum_{i=1}^n f(x_i)$$gdzie $h$ oznacza szerokość prostokąta a $f(x_i)$ kolejne wartości wysokości prostokątów,
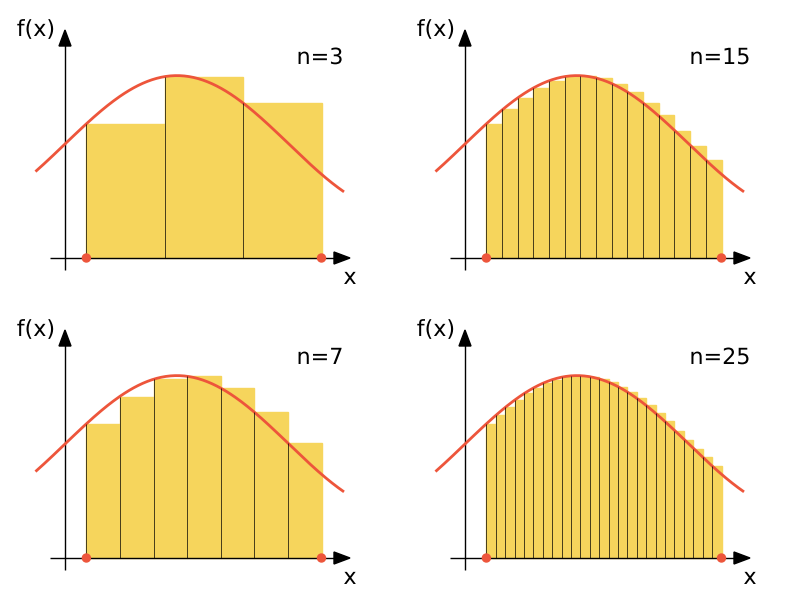
Dokładność metody prostokątów zależy przedewszytkim od liczby podziałów. Na rysunku przedstawiono wpływ liczby podziałów na przybliżenie obszaru znajdującego się pod funkcją.
Opis algorytmu dla metody prostokątów
Parametrami wejściowymi do algorytmu są
• $f(x)$ - funkcja podcałkowa
• $a, b$ - przedział całowania
• $n$ - liczba podziałów przedziału całkowania
1. Oblicz szerokość podprzedziału
$$h = \cfrac{b-a}{n}$$2. Zdefiniuj zmienną wynikową $I$ i przypisz jej wartość $0$.
3. Dla każdego podprzedziału $i=1,2,3,...,n$
• Oblicz kolejną wartość położenia prostokąta
$$x_i = a + (i-1)h$$• Oblicz pole prostokąta i dodaj otrzymany wyniki do zmiennej wynikowej
$$I_i = f(x_i) h, \quad I = I + I_i$$Ostateczny wynik $I$ reprezentuje przybliżoną wartość całki z funkcji $f(x)$ na przedziale $[a, b]$
Przykład działania
Prześledźmy wszystkie kroki algorytmu do obliczenia całki
$$\int_1^4 3x^2 dx = x^3|_1^4 = (4^3-1^3) = 64-1 = 63.$$W pierwszym kroku ustalmy $n$ czyli liczbę przedziałów na który podzielmy obszar całowania. Zdefiniujmy również dwie stałe związane z granicami całkowania oraz zmienną związaną z wartość naszej całki $I$.
Przypiszmy tej zmiennej wartość 0.
Obliczmy szerokość pojedynczego przedziału $h$
$$h = (4-1)/3 = 1$$Obliczmy położenie pierwszego prostokąta $i=1$
$$x_1 = a + (i-1)h = 1 + (1-1)\cdot 1 = 1$$Obliczmy pole pierwszego prostokąta
$$p_1 = f(x_1) \cdot h = 3x_1^2 \cdot h = 3\cdot 1^2 \cdot 1 = 3$$Nasza całka na tym etapie obliczeń wynosi
$$I = I + p_1 = 0 + 3 = 3$$Powtórzmy powyższe kroki dla drugiego prostokąta $i=2$
$$x_2 = a + (i-1)h = 1+(2-1)\cdot 1 = 2$$Pole będzie równe
$$p_2 = f(x_2) \cdot h = 3x_2^2 \cdot h = 3\cdot 2^2 \cdot 1 = 12$$Całka na tym etapie będzie równa
$$I = I + p_2 = 3+12 = 15$$Dla ostatniego prostokąta $i=3=n$ mamy
$$x_3 = a + (i-1)h = 1+(3-1)\cdot 1 = 3, \quad p_3 = f(x_3) \cdot h = 3x_3^2 \cdot h = 3 \cdot 3^2 \cdot 1 = 27$$Całka jest więc równa
$$I = I + p_3 = 15 + 27 = 42$$Uzyskany wynik z metody prostokątów jest bardzo niedokładny. Zwiększenie liczby przedziałów $n$ pozwala na osiągnięcie lepszego wyniku.
# Przykład
Opracuj program który oblicza wartość całki oznaczonej dla funkcji $f(x)$ na przedziale $[a,b]$ wykorzystując metodę prostokątów. $a= -2, \quad b=6, \quad n=12$.
$$f(x) = -2x^2 + 10x +30.$$Obliczoną wartość całki porównaj z wartością dokładną.
Metoda trapezów
Metoda trapezów to kolejna popularna technika całkowania numerycznego. Podobnie jak w przypadku metody prostokątów, metoda trapezów polega na przybliżeniu całki przez sumowanie obszarów trapezów utworzonych pod krzywą funkcji.
Metoda trapezów jest bardziej dokładna niż metoda prostokątów, ale nadal jest stosunkowo prosta do zrozumienia i implementacji. Podobnie jak w przypadku innych metod całkowania numerycznego, dobór odpowiedniej liczby podprzedziałów $n$ wpływa na dokładność wyniku, a większa liczba podprzedziałów zazwyczaj prowadzi do dokładniejszej aproksymacji.
$$I(f) = \int_a^b f(x) dx \approx h\sum_{i=1}^{n} \cfrac{f(x_i)+f(x_{i+1})}{2}$$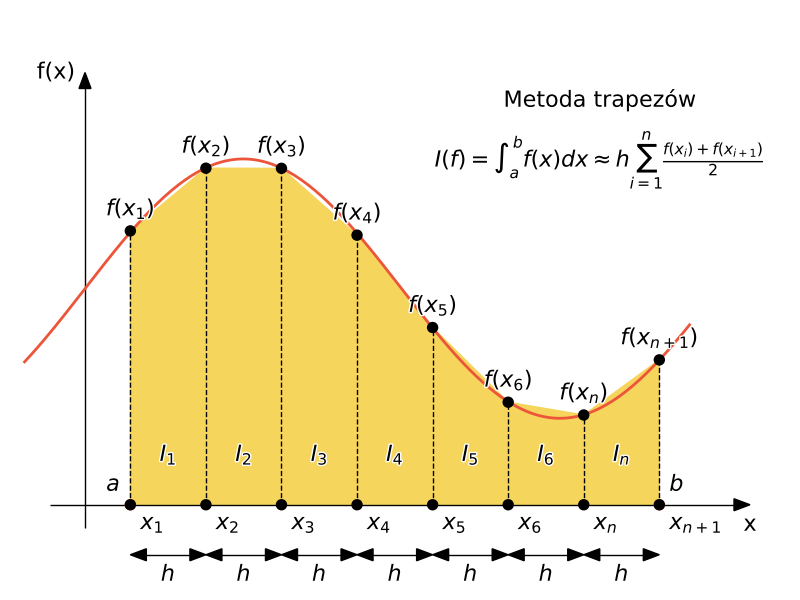
# Przykład
Opracuj program który oblicza wartość całki oznaczonej dla funkcji $f(x)$ na przedziale $[a,b]$ wykorzystując metodę trapezów. $a= -2, \quad b=6, \quad n=12$.
$$f(x) = sin^2(x) + \cfrac{10}{3}\sqrt{cos^2(x)+1}.$$