Metody Obliczeniowe

Wstęp

Różniczkowanie numeryczne to proces przybliżonego obliczania pochodnych funkcji za pomocą metod numerycznych. Jest stosowane, gdy:
• funkcja jest znana tylko w postaci danych dyskretnych (np. pomiarów).
• analityczne obliczenie pochodnej jest trudne lub niemożliwe.

Istnieją dwa podstawowe sposoby różniczkowania numerycznego. Pierwszy z nich to metoda różnic skończonych, która opiera się na przybliżeniu pochodnej funkcji za pomocą skończonych różnic w zdyskretyzowanej przestrzeni. Wyprowadzenie tej metody może być oparte na ilorazie różnicowym lub rozwinięciu funkcji w szereg Taylora. Drugi sposób polega na różniczkowaniu funkcji aproksymującej, gdzie punkty są aproksymowane wyrażeniem, które można łatwo różniczkować.

Metoda Różnic Skończonych

Podstawą różniczkowania numerycznego są wzory przybliżające pochodne z wykorzystaniem różnic skończonych. Główne metody to:
• Różnica w przód (forward difference):
• Różnica wstecz (backward difference):
• Różnica centralna (central difference):

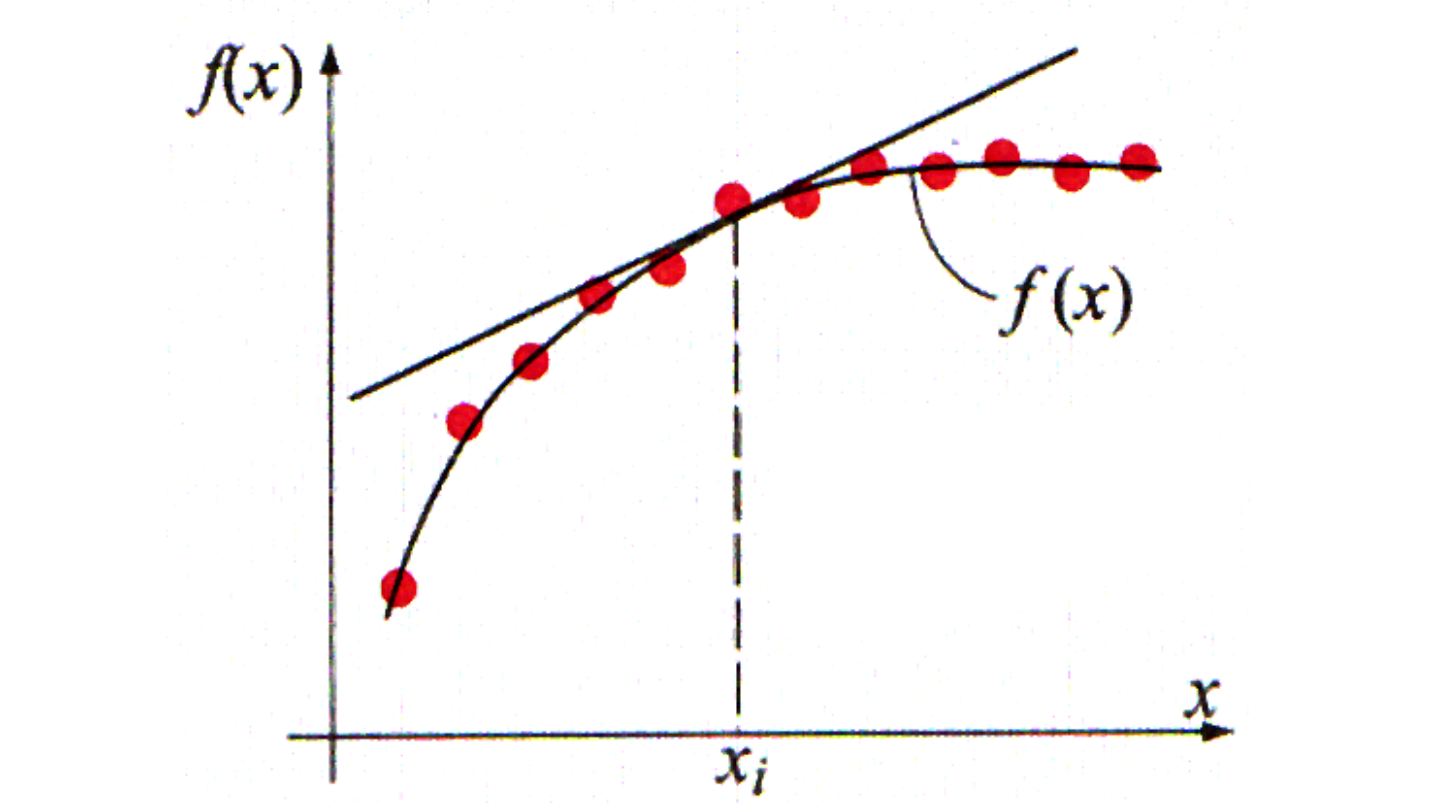
Różnica w przód oblicza przybliżenie pierwszej pochodnej funkcji $f(x)$ w punkcie $x$ korzystając z wartości funkcji w tym punkcie oraz w punkcie $x+h$ (przesunięcie o krok $h$).

$$f'(x) \approx \frac{f(x + h) - f(x)}{h}.$$

Różnica w tył oblicza przybliżenie pierwszej pochodnej funkcji $ f(x) $ w punkcie $ x $ korzystając z wartości funkcji w tym punkcie oraz w punkcie $x-h$. Różnica w tył działa w sposób analogiczny do różnicy w przód, ale bierze pod uwagę punkty "na lewo" od $x$.

$$f'(x) \approx \frac{f(x) - f(x - h)}{h}.$$

Różnica centralna oblicza przybliżenie pierwszej pochodnej funkcji $f(x)$ w punkcie $x$, wykorzystując 2 symetrycznie położone punkty $x-h$ oraz $x+h$.

$$f'(x) \approx \frac{f(x + h) - f(x - h)}{2h}.$$

Opis algorytmu dla metody różnic skończonych w przód

1. Parametry wejściowe
- funkcja $f(x)$ dla której chcemy wyznaczyć pochodną
- przedział $[a,b]$ na którym obliczana jest pochodna
- krok metody $h$

2. Dla każdego punktu oblicz
- jego pozycję $x_i = a + ih$
- wartosć funkcji w tym punkcie $f_i = f(x_i)$
- pochodną ze wzoru

$$f'(x_i) = \cfrac{f(x_{i}+h) - f(x_i)}{h}$$

# Przykład

Wyznacz pochodną funkcji $f(x) = \sin(x)$ w przedziale $[0, \pi/2]$ stosując metodę różnic skończonych w przód.

// Funkcja analityczna
function y = f(x)
    y = sin(x)
end
// Parametry
x = 0:0.1:%pi/2 // Przedział [0, pi/2]
h = 0.1          // Krok różniczkowania
// Różnica w przód
n = length(x)
dy = zeros(1, n-1)
for i = 1:n-1
    dy(i) = (f(x(i) + h) - f(x(i))) / h
end
// Wyświetlenie wyników
disp("Pochodna:")
disp(dy)

Pochodna drugiego rzędu

Metodę różnic skończonych możemy również stosować do obliczania pochodnych wyższych rzędów. Dla przykładu, poniżej zamieszczono wzór dla pochodnej drugiego rzędu.
Druga pochodna - różnica centralna

$$f''(x) \approx \frac{f(x + h) - 2f(x) + f(x - h)}{h^2}.$$

# Przykład

Wyznacz drugą pochodną funkcji $f(x) = 3e^x$ w przedziale $[-3,3.5]$ stosując metodę różnic skończonych.

# Przykład

Wyznacz pochodną funkcji $f(x) = x^2 + sin(3x)$ w przedziale $[-2,2]$ stosując różnice w przód, różnice w tył oraz różnice centralne. Narysuj trzy wykresy pochodnych. Wynik porównaj z rozwiązaniem analitycznym.

Funkcja diff

Funkcja diff w Scilab służy do obliczania różnic skończonych w tablicach danych numerycznych. W praktyce wykorzystuje się ją do przybliżania pochodnych numerycznych lub analizy różnic między kolejnymi elementami wektora/macierzy.

y = diff(x)

Argumentem funkcji diff jest wektor lub macierz dla którego obliczane są różnice skończone. Krok $h$ jest równy 1.

# Przykład

x = linspace(0,1, 100)
disp(x)
h = x(2)-x(1)
y = 0.5*x.^2
dy = diff(y,1)/h
disp(length(x))
disp(length(dy))
xp = x(1:$-1)
plot(xp,dy)
xgrid()