Interpolacja wielomianowa
Interpolacja wielomianowa to metoda matematyczna używana do znalezienia wielomianu, który przechodzi przez zestaw danych punktów. W skrócie, interpolacja wielomianowa pozwala na stworzenie wielomianu stopnia n-1 (gdzie n to liczba punktów danych), który dokładnie przechodzi przez te punkty.
Powyższy uklad równań możemy zapisać w formie macierzowej jako
$$\left[ \begin{array}{cccccccc} 1 & x_0 & x_0^2 & ... & x_0^n \\ 1 & x_1 & x_1^2 & ... & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & ... & x_n^n \\ \end{array} \right] \cdot \left[ \begin{array}{c} a_0\\ a_1\\ \vdots\\ a_n \end{array} \right] = \left[ \begin{array}{c} y_0\\ y_1\\ \vdots\\ y_n \end{array} \right]$$# Przykład
Wyznacz współczynniki wielomianu drugiego stopnia $f(x) =a_0 + a_1x +a_2x^2$ który przechodzi przez zadane trzy punkty: $(-2,1)$, $(0,0)$, $(2,1)$.
Podstawmy pierwszy punkt do naszego wielomianu
$$f(x=-2) = a_0 + a_1 \cdot (-2) + a_2 (-2)^2 = 1$$Dla drugiego punktu mamy
$$f(x=0) = a_0 + a_1 \cdot 0 + a_2 0^2 = 0$$a dla ostatniego
$$f(x=2) = a_0 + a_1 \cdot 2 + a_2 2^2 = 1$$Dostajemy więc następujący układ równań
$$\begin{array}{cccccccc} a_0-2a_1 + 4a_2&=& 1 \\ a_0-0a_1 + 0a_2&=& 0 \\ a_0+2a_1 + 4a_2&=& 1 \\ \end{array}$$Rozwiązaniem tego układu są liczby
$$a_0=0, \quad a_1=0, \quad a_2 = \cfrac14$$
# Przykład
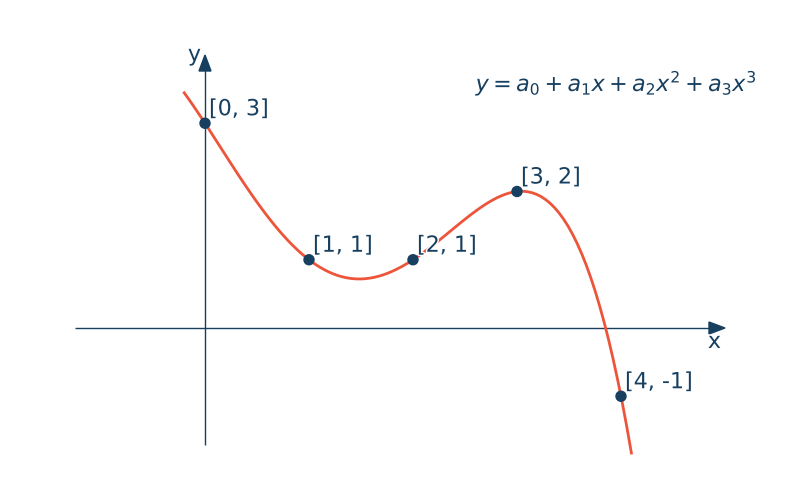
Wyznacz współczynniki wielomianu trzeciego stopnia $f(x)$ który przechodzi przez zadane cztery punkty: $(1,1)$, $(2,2)$,$(3,2)$,$(4,-1)$