Wprowadzenie do LibreOffice
LibreOffice to darmowy pakiet biurowy zawierający narzędzia do edycji tekstu, arkuszy kalkulacyjnych, prezentacji, baz danych i innych. Jest to alternatywa dla komercyjnych pakietów biurowych, takich jak Microsoft Office, i działa na wielu systemach operacyjnych, w tym Windows, macOS i Linux. W kontekście obliczeń macierzowych, LibreOffice Calc jest potężnym narzędziem, które umożliwia wykonywanie szerokiego zakresu operacji matematycznych, w tym na macierzach.
Definicja macierzy
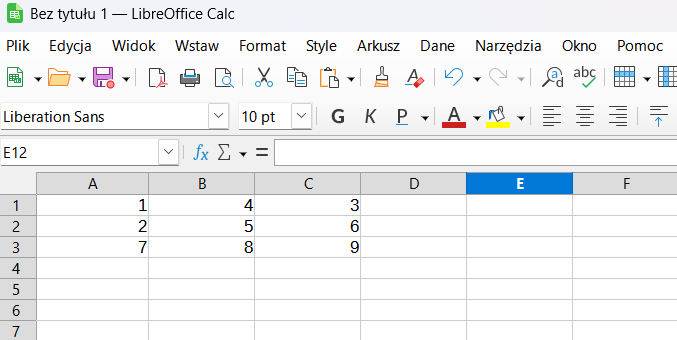
Aby zdefiniować macierz w LibreOffice Calc, wprowadź dane do arkusza kalkulacyjnego w formacie tabelarycznym. Każda komórka reprezentuje element macierzy.
# Przykład:
A1: 1 B1: 4 C1: 3
A2: 2 B2: 5 C2: 6
A3: 7 B3: 8 C3: 9
Sumowanie elementów wektora
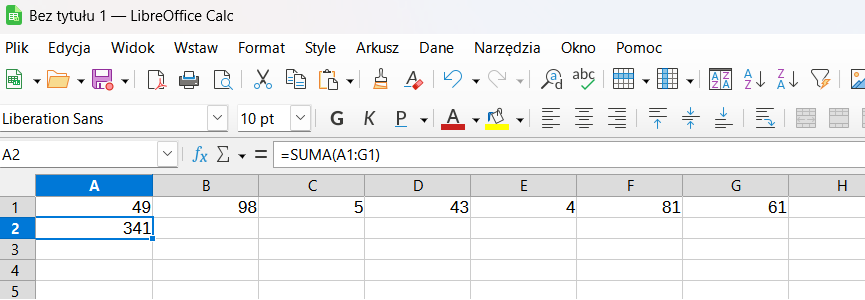
Funkcja SUMA (w wersji angielskiej SUM ) służy do sumowania wartości z wybranego zakresu komórek. Jest jedną z najczęściej używanych funkcji w arkuszach kalkulacyjnych, ponieważ pozwala szybko i łatwo obliczyć sumę liczb znajdujących się w określonym obszarze.
Generowanie liczb losowych
Do wygenerowania losowej liczby z danego zakresu możemy użyć funkcji LOS.ZAKR(a; b) (w wersji angielskiej RANDBETWEEN(A;B), gdzie liczby a i b określają odpowiednio dolny i góry zakres z którego losowana jest liczba. Argumenty funkcji oddzielamy z użyciem średnika!
=SUMA(A1:G1)
# Przykład
Wygeneruj 10 losowych liczb z zakresu od 1 do 20 a następnie dodaj je wszystkie z użyciem polecenia SUMA.
Wyznacznik macierzy
Wyznacznik macierzy obliczamy z wykorzystaniem funkcji MACIERZ.WYZNACZNIK (w angielskiej wersji MDETERM )
Mnożenie macierzowe
Funkcja MACIERZ.ILOCZYN (w wersji angielskiej MMULT )służy do wykonywania operacji mnożenia macierzy. Przyjmuje dwa zakresy komórek jako argumenty, które reprezentują macierze, i zwraca wynikową macierz, będącą iloczynem tych macierzy. Mnożenie macierzy odbywa się poprzez mnożenie elementów wierszy pierwszej macierzy przez odpowiednie elementy kolumn drugiej macierzy i sumowanie tych iloczynów. Aby użyć tej funkcji, zaznacz odpowiedni zakres komórek na arkuszu, wpisz formułę MACIERZ.ILOCZYN i wprowadź zakresy macierzy do mnożenia.
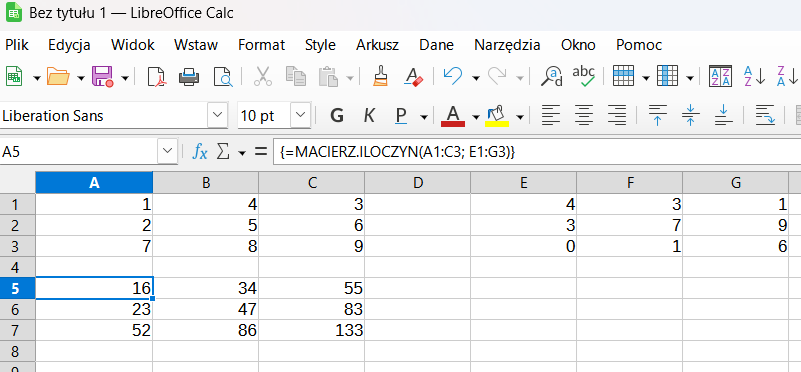
# Przykład:
=MACIERZ.ILOCZYN(A1:C3; E1:G3)
gdzie A1:C3 to pierwsza macierz, a E1:G3 to druga macierz.
Rozwiązywanie Układów Równań Liniowych
Układ równań liniowych można rozwiązać za pomocą funkcji MACIERZ.ODW (w wersji angielskiej MINVERSE ) i MACIERZ.ILOCZYN .
Funkcja MACIERZ.ODW służy do obliczania macierzy odwrotnej. Przyjmuje jeden argument, którym jest zakres komórek reprezentujący kwadratową macierz, i zwraca macierz odwrotną. Aby użyć tej funkcji, zaznacz zakres komórek o tej samej liczbie wierszy i kolumn.
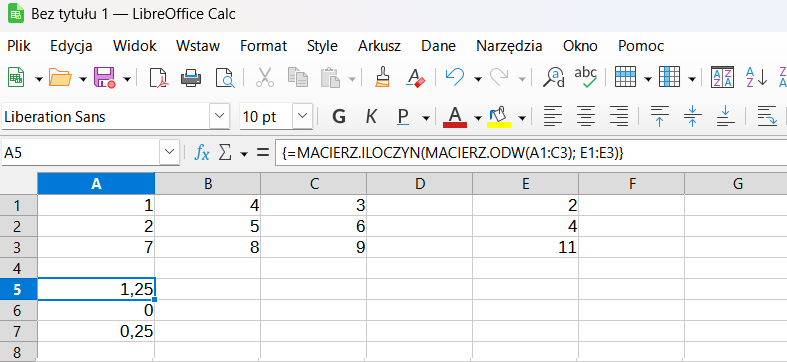
# Przykład:
=MACIERZ.ILOCZYN(MACIERZ.ODW(A1:C3); E1:E3)
gdzie A1:C3 to macierz współczynników, a E1:E3 to wektor prawej strony układu równań.
Generowania wektora
Aby wygenerować wektor zawierający liczby z zakresu od $a$ do $b$ z krokiem $c$ należy wpisać wartość początkową w komórkę np. A2. W komórkę A3 wpisujemy formułę
$$= A2 + c$$Następnie należy zaznaczyć komórkę A3 i przeciągnąć w dół uchwyt wypełnienia (mały kwadrat w prawym dolnym rogu komórki), aż osiągnie wartość $b$
# Przykład
Wygeneruj wektor liczb z przedziału od -5 do 4 z krokiem 0.5
Tablicowanie funkcji
Tablicowanie funkcji to proces tworzenia tabeli wartości funkcji. Aby utworzyć taką tablę dla danej funkcji $f(x)$ należy
• wygenerować zbiór zawierający dziedzinę funkcji - wektor x
• wygenerować wektor $y$ na podstawie zadanego wzoru
Jeżeli założymy że w kolumnie A znajduje sie wektor x to aby wegeneować zbiór wartosci funkcji (wektor y) należy w kolumnie B wpisać formułę określającą wzór funkcji np.
$$= 2*A1$$gdzie A1 oznacza adres pierwszej komórki w której znajduje się wartość początkowa wektora x. Aby otrzymać pozostałe wartości funkcji należy przeciągnąć formułę w dół aż do ostatnie komórki wektora x. W ten sposób otrzymamy dwa wektory
• wektor argumentów funkcji $x$
• wektor wartości funkcji $y$
# Przykład
Wykonaj tablicowanie funkcji
$$y = sin(x) + 0.5*x$$dla wartości argumentu $x \in (-6,6)$ z krokiem 0.5
W kolumnie B utwórz serię danych zawierających wektor $x$ natomiast w kolumnie C zbiór wartości (wektor y).
Tworzenie wykresu funkcji
Wykresy funkcji tworzymy za pomocą opcji Wstaw-Wykres ( w wersji angielskiej Insert-Chart ) wybieranej z menu głównego programu. Po przygotowaniu tabeli z wartościami (np. kolumna A – x, kolumna B – y) można w prosty sposób utworzyć wykres ilustrujący zależność między tymi danymi.
W pierwszym kroku musimy zaznaczyć dane (obszar danych) który ma zostać przedstawiony na wykresie. Następnie uruchamiamy kreatora wykresu
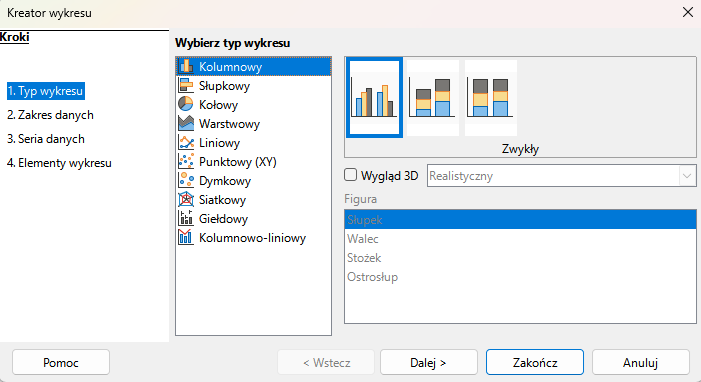
Kreator pozwala na ustawienie wielu parametrów wykresu tak jak typ, zakres danych oraz elementy graficzne które mają pojawić się na wykresie.
# Przykład
Narysuj wykresy funkcji kwadratowej
$$y = ax^2$$dla trzech wartości parametru $a$ zgodnie z poniższą tablą
| $a_1$ | $a_2$ | $a_3$ |
|---|---|---|
| 0.4 | 1.0 | 2.0 |