Układy równań liniowych
Równania liniowe to równania, w których najwyższym stopniem każdego z członów jest 1. Układy równań liniowych to zestawy dwóch lub więcej równań liniowych, które mają wspólne zmienne. Ogólnie układ równań liniowych może być zapisany w postaci
$$\begin{array}{ccccccc} a_{11}x_1 &+& a_{12}x_2&+&a_{13}x_2&+&...&+&a_{1n}x_n&=b_1\\ a_{21}x_1 &+& a_{22}x_2&+&a_{23}x_2&+&...&+&a_{2n}x_n&=b_2\\ a_{31}x_1 &+& a_{32}x_2&+&a_{33}x_2&+&...&+&a_{3n}x_n&=b_3\\ \vdots & & \vdots&&\vdots& & \ddots & &\vdots& \vdots\\ a_{n1}x_1 &+& a_{n2}x_2&+&a_{n3}x_2&+&...&+&a_{nn}x_n&=b_n\\ \end{array}$$Powyższy układ równań możemy zapisać w postaci macierzowej jako
$$\a\x=\b$$ $$\a = \left[ \begin{array}{ccccccc} a_{11} & a_{12} & a_{13} & ... & a_{1n} \\ a_{21} & a_{22} & a_{23} & ... & a_{2n} \\ a_{31} & a_{32} & a_{33} & ... & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots& \\ a_{n1} & a_{n2} & a_{n3} & ... & a_{nn} \\ \end{array} \right], \quad \x = \left[ \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \\ \end{array} \right] \quad \b = \left[ \begin{array}{c} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_n \\ \end{array} \right]$$gdzie $a$ jest macierzą kwadratową o wymiarach $n\times n$ zawierającą wspłczynniki $a_{ij}$ stojące przy niewiadomych, wektor $\x$ o wymiarze $n\times 1$ zawiera niewiadome $x_i$, wektor $\b$ zawiera współczynniki stojące po prawej stronie równań $b_i$.
W powyższym zapisie wykorzystaliśmy wzór na mnożenie macierzy przez wektor
$$\sum_{j=1}^n a_{ij}v_j = b_i, \quad \text{dla} \quad i=1,2,\ldots, n$$Dla przykładu, jeżeli $n=2$ dostajemy układ równań liniowyh z dwoma niewiadomymi $x_1$ oraz $x_2$.
$$\begin{array}{ccccccc} a_{11}x_1 &+& a_{12}x_2& = b_1\\ a_{21}x_1 &+& a_{22}x_2& = b_2\\ \end{array}$$Rozwiązanie układu równań liniowych oznacza znalezienie wektora $\x$, który spełnia wszystkie równania jednocześnie.
Rozwiązanie takiego układu może być jednoznaczne, niejednoznaczne lub nie istnieć w zależności od relacji między równaniami. Można użyć różnych metod, takich jak eliminacja Gaussa, metoda macierzy odwrotnej, czy metoda Jacobiego, aby znaleźć rozwiązania układu równań liniowych.
Metoda rozwiązania układu równań liniowych
Rozwiązanie układu równań liniowych możemy otrzymać jako
$$\x = \a^{-1} \b$$gdzie $\a^{-1}$ oznacza macierz odwrotną do macierzy $\a$.
Scilab posiada specjalną funkcję, która pozwala na obliczanie macierzy odwrotnej
inv(a)
# Przykład
//definicja macierzy a
a = zeros(5,5) + eye(5,5)
//definicja wektora b
b = (1:5)'
//rozwiązanie układu równań
x = inv(a)*b
//sprawdzenie
disp(a*x-b)
# Przykład
Rozwiąż podany układ równań
$$\begin{array}{ccccccccc} 4x_1 & + & 2x_2 & + & 3x_3 & + & 7x_4 &=& 3\\ 8x_1 & + & 9x_2 & + & x_3 & - & 2x_4 &=& 8\\ x_1 & - & 2x_2 & + & 7x_3 & - & 5x_4 &=& -3\\ -2x_1 & - & 5x_2 & + & 6x_3 & - & 8x_4& =& -2\\ \end{array}$$# Przykład
Zbuduj układ równań liniowych dla podanej kratownicy korzystając z metody równoważenia węzłów. Następnie rozwiąż układ i wyświetl siły w każdym pręcie kratownicy
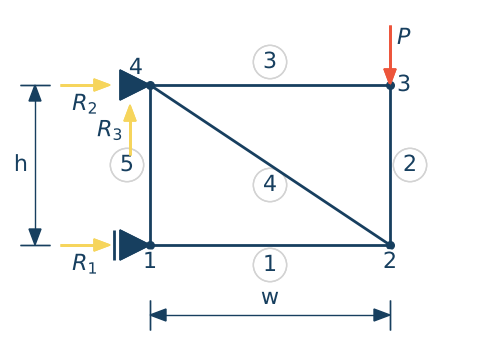
# Przykład
Zbuduj układ równań liniowych dla podanej kratownicy korzystając z metody równoważenia węzłów. Następnie rozwiąż układ i wyświetl siły w każdym pręcie kratownicy
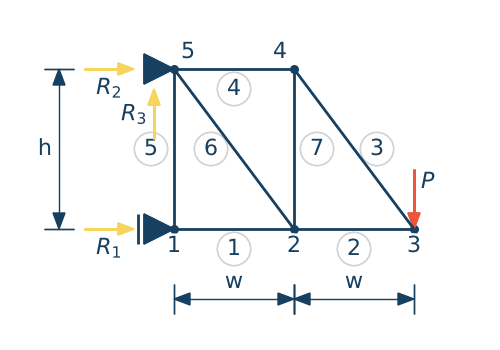
# Przykład
Zbuduj układ równań liniowych dla podanej kratownicy korzystając z metody równoważenia węzłów. Następnie rozwiąż układ i wyświetl siły w każdym pręcie kratownicy
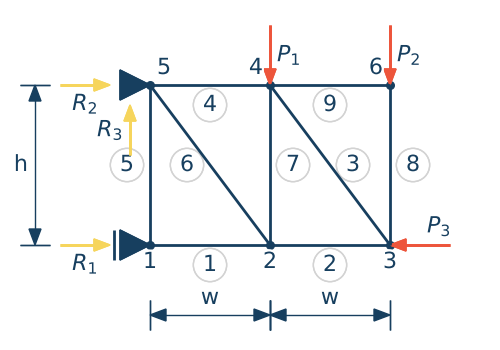
Rozwiązanie
Wyznaczenie reakcji w podporach
$$\sum F_x = 0 \quad \Rightarrow \quad -R_1 -R_2 + P_3 = 0$$ $$\sum F_y = 0 \quad \Rightarrow \quad R_3 = P_1 + P_2$$ $$\sum M_1 = 0 \quad \Rightarrow \quad R_2 \cdot h + P_1 \cdot w + P_2 \cdot 2w = 0$$Budowa układu równań