Instrukcja iteracyjna - pętla for
Pętla for to struktura kontrolna w programowaniu, która umożliwia powtarzanie określonych instrukcji lub bloku kodu przez określoną liczbę razy. W większości języków programowania pętla for jest używana do iteracji przez kolekcje elementów, takie jak tablice, listy czy zakresy liczb.
Sposób działania:
• zmienna (sterująca) i zostaje określona jako tablica kolejnych liczb naturalnych od $1$ aż do $n$
• dla każdej kolejnej wartości zmiennej i wykonywana jest instrukcja zawarta między słowami kluczowymi for i end
• iteracje wykonywane są $n$ razy
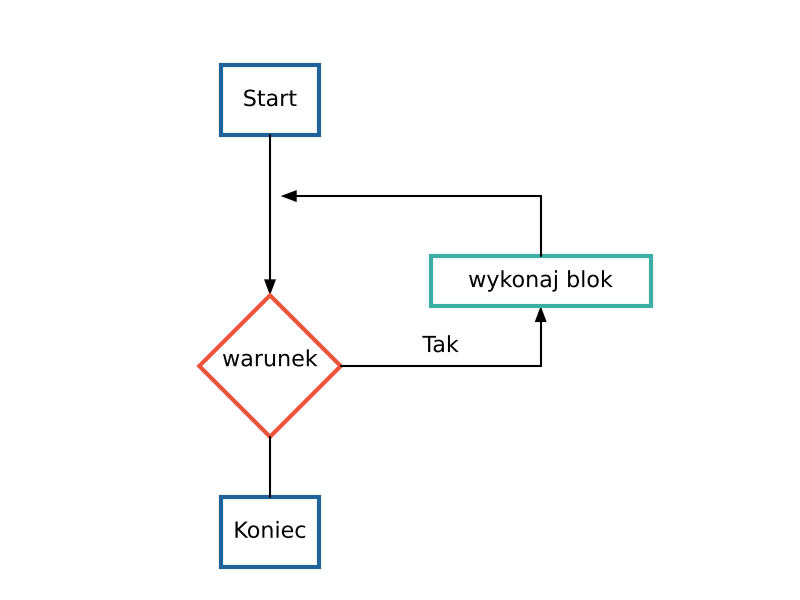
W programie Scilab instrukcję pętli for zapisujemy jak poniżej. Wewnątrz pętli zapisujemy instrukcje które mają być wykonane n-razy.
for i=1:n
//instrukcje do wykonania
end
Użycie pętli pozwala na skrócenie zapisu różnych instrukcji. Dla przykładu jeżeli chcemy wyświetli w konsoli swoje imię 10 razy to moglibyć napisać taką instrukcję
disp("marcin")
disp("marcin")
disp("marcin")
disp("marcin")
disp("marcin")
disp("marcin")
disp("marcin")
disp("marcin")
disp("marcin")
disp("marcin")
Identyczny efekt uzyskamy gdy zapiszemy to z użyciem pętli
for i=1:10
disp("marcin")
end
Za kolejny przykład zastosowania pętli for może posłużyć nam instrukcja do wyświetlania kolejnych liczb naturalnych. Bez użycia pętli zapisalibyś to w następujący sposób
disp(1)
disp(2)
disp(3)
disp(4)
disp(5)
disp(6)
i tak dalej. Z użyciem pętli możemy to zapisać znacznie krócej i ogólniej
for i=1:10
disp(i)
end
# Przykład
Wygeneruj wektor którego elementy zawierają kwadraty kolejnych liczb naturalnych zaczynając od 1. Długość wektora jest równa 10.
clc // czyszczenie konsoli
clear // czyszczenie pamięci (zmiennych)
v = zeros(1,10) // utworzenie wektora o długości 10 wypełnionego zerami
for i=1:10
v(i) = i^2
end
disp(v)
// [1 4 9 16 25 36 49 64 81 100]
# Przykład
Zapisz instrukcję która, oblicza sumę kwadratów wszystkich elementów wektora
$$\v = [1,2,3,\ldots, 50]$$v = 1:50
n = length(v)
suma = 0.0
for i=1:n
suma = suma + v(i)^2
end
disp(suma) //42925
# Przykład
Zapisz instrukcję która generuje wektor $\v$ o długości 20 którego wartość dla danej kolumny $i$ jest równa
$$v_i = \sin^2(i^2)$$czyli
| i=1 | i=2 | i=3 | ... | i=20 |
|---|---|---|---|---|
| $\sin^2(1)$ | $\sin^2(4)$ | $\sin^2(9)$ | ... | $\sin^2(20^2)$ |
# Przykład
Wygeneruj macierz $\A$ o wymiarze $5 \times 8$ której elementy równe są sumie kwadratów numeru wiersza i kolumny w której znajduje się dany element.
Dla przykładu wartości macierzy $\A$ w zależności od numeru wiersza i kolumny są równe
$$A(2,3) = 2^2 + 3^2= 4+9 = 13$$ $$A(4,5) = 4^2 + 5^2= 16+25 = 41$$ $$\A = \begin{bmatrix} 2 & 5 & 10 & ... & 65 \\ 5 & 8 & 13 & ... & 68 \\ 10 & 13 & 18 & ... & 73 \\ ... & ... & ... & ... & ...\\ 26 & 29 & 34 & ... & 89\\ \end{bmatrix}$$# Przykład
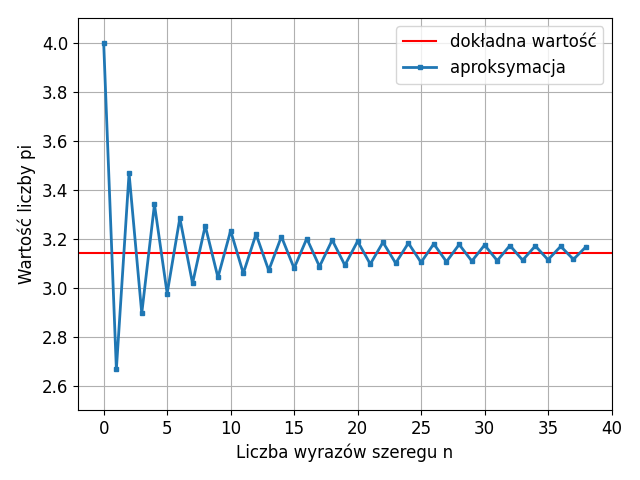
Napisz program, który aproksymuje wartość liczby $\pi$ za pomocą szeregu Leibniza:
$$\pi \approx 4 \cdot \sum_{k=0}^{n} \frac{(-1)^k}{2k + 1}$$gdzie:
• $n$ to liczba iteracji (podana przez użytkownika),
• $k$ to numer iteracji w pętli.
Interaktywny przykład, który angażuje użytkownika. Program poprosi o wpisanie imienia, a potem powtórzy je kilka razy, używając pętli for.
// Prosty program z pętlą for i interakcją
imie = input("Podaj swoje imię: ", "string");
// Powtórz imię 5 razy
disp("Twoje imię powtórzone 5 razy:");
for i = 1:5
disp(string(i) + ". " + imie);
end
• input("Podaj swoje imię: ", "string") - Pobieramy od użytkownika tekst (imię).
• for i = 1:5 - Pętla for iteruje od 1 do 5.
• disp(string(i) + ". " + imie) - Funkcja disp wyświetla tekst. string(i) zamienia liczbę i na tekst, a operator + łączy teksty
Instrukcja warunkowa if-else
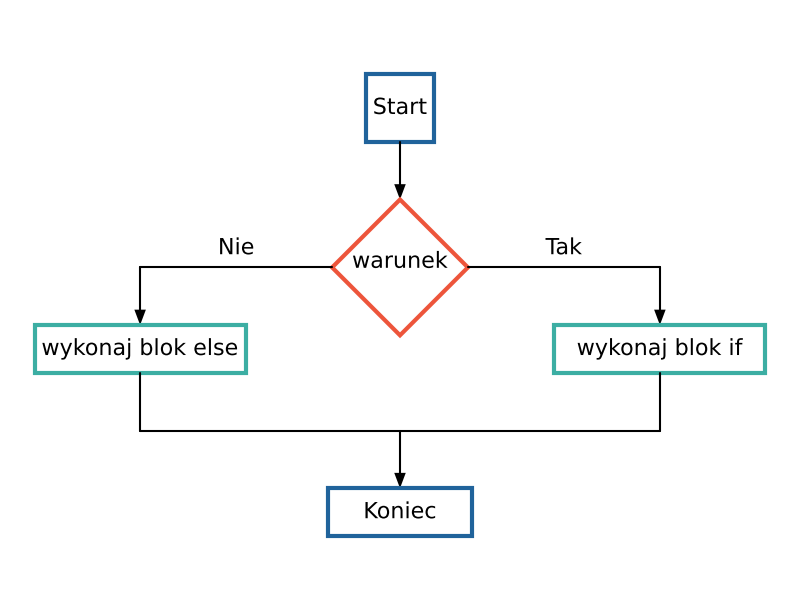
Instrukcja warunkowa if-else to konstrukcja która pozwala na wykonanie różnych bloków kodu w zależności od spełnienia warunku logicznego. Ogólna struktura instrukcji if-else wygląda następująco
if warunek
//do something
else
//do something
end
• Blok kodu pod if jest wykonywany, jeśli warunek (wyrażenie logiczne) jest prawdziwy.
• Blok kodu pod else jest wykonywany, jeśli warunek jest fałszywy.
# Przykład
Zapisz instrukcję która sprawdza czy wartość zmiennej jest równa 1. Jeżeli wartość zmiennej jest równa 1 wyświetl napis "Prawda", w przeciwnym przypadku "Fałsz".
a=1
if a==1
disp("Prawda")
else
disp("Fałsz")
end
W Scilab, w konstrukcjach if-else, można stosować różne typy warunków logicznych. Oto opis podstawowych operatorów relacyjnych i logicznych, które można używać:
| Operator | Opis | Przykład |
|---|---|---|
| == | Równość | a == b |
| ~= | Różne | a ~= b |
| > | Większe niż | a > b |
| < | Mniejsze niż | a < b |
| >= | Większe lub równe | a >= b |
| <= | Mniejsze lub równe | a <= b |
# Przykład
• Zapisz instrukcję która sprawdza czy dana liczba jest większa od 5.
x=10
if x>5
disp("x jest większe niż 5")
else
disp("x nie jest większe niż 5")
end
W tym przypadku, jeśli wartość zmiennej x jest większa niż 5, zostanie wykonany pierwszy blok kodu
disp("x jest większe niż 5").
W przeciwnym razie, gdy warunek nie jest spełniony, zostanie wykonany drugi blok kodu
disp("x nie jest większe niż 5")
# Przykład
Zapisz instrukcję która generuje wektor postaci
$$a = [1,2,3,..., 100, 99, 98, ..., 1]$$n=199
a = zeros(1,n)
for i=1:n
if i<101
a(i)=i
else
a(i)=n+1-i
end
end
disp(a)
W powyższym przypadku definiujemy w pierwszej kolejności wektor o długości 199 wypełniony zerami. Następnie zapisujemy konstrukcję for aby iterować po wszystkich elementach tego wektora. Zmienną sterującą i wykorzystujemy w warunku if aby zmienić formułę na podstawie której wstawiane są liczby do wektora. Jeśli zmienna i jest mniejsza niż 101 to do wektora wstawiamy liczbę
a(i)=i
w przeciwnym wypadku czyli dla i większych lub równych 101 używamy drugiej formuły
a(i)=n+1-i
# Przykład
Napisz program, który znajduje wszystkie liczby pierwsze w zakresie od 2 do $n$, gdzie $n$ jest podawane przez użytkownika.
Funkcje
Funkcje w programowaniu to bloki kodu, które są zorganizowane w sposób, który umożliwia ich wielokrotne użycie. Funkcje służą do grupowania zestawu instrukcji w jedną jednostkę, co sprawia, że kod staje się bardziej czytelny, modularny i łatwiejszy do zarządzania.
Ogólna struktura definicji funkcji w Scilab wygląda następująco
function [w1, w2, ...] = nazwa_funkcji(ar1, ar2, ...)
// Ciało funkcji
endfunction
• function - Słowo kluczowe rozpoczynające definicję funkcji.
• [w1, w2, ...] - Opcjonalne zmienne wynikowe, które funkcja może zwrócić.
• nazwa_funkcji - Nazwa funkcji, którą definiujesz.
• (arg1, arg2, ...) Argumenty, czyli wartości, które przekazywane są do funkcji.
• // Ciało funkcji - Komentarze lub instrukcje wykonujące konkretne zadania.
• endfunction - Słowo kluczowe kończące definicję funkcji.
# Przykład
Zapisz funkcję realizującą dodawanie dwóch liczb
function suma = dodaj(a, b)
suma = a + b
endfunction
// wywołanie funkcji
wynik = dodaj(3, 5)
disp(wynik)
W tym przykładzie funkcja dodaj przyjmuje dwa argumenty a i b i zwraca ich sumę. Funkcję tę można następnie wywołać z argumentami 3 i 5, a wynik zostanie wyświetlony.
# Przykład
Zapisz funkcję która oblicza długość wektora o trzech współrzędnych.
function dlugosc = obliczDlugoscWektora(x, y, z)
dlugosc = sqrt(x^2 + y^2 + z^2)
endfunction
//
dlugoscWektora = obliczDlugoscWektora(3, 4, 5)
disp(dlugoscWektora)
# Przykład
Zapisz funkcję która oblicza pole przekroju poprzecznego rury na podstawie dwóch argumentów którymi są: średnica zewnętrza $d_1$ oraz średnica wewnętrzna $d_2$. Wykorzystując konstrukcję warunkową sprawdź poprawność wprowadzonych danych czyli czy $d_1 > d_2$. Jeżeli warunek nie jest spełniony funkcja powinna zwrócić wartość $0$.
# Przykład
Zapisz funkcję która oblicza sumę szeregu w zależności od liczby jego wyrazów.
$$\sum_{i=1}^{n} \cfrac{100}{(3i-2)(3i+1)}$$Następnie wywołaj opracowaną funkcję dla argumentów $n=2$, $n=10$ oraz $n=1000$.
# Przykład
Opracuj program który rozwiązuje równanie kwadratowe o zadanych współczynnikach $a$, $b$ i $c$.
$$ax^2 + bx + c = 0$$# Przykład
Opracuj funkcje, która oblicza zysk z lokaty dla następujących parametrów
• k0 - kapitał początkowy
• op - oprocentowanie w stosunku rocznym
• lata - liczba lat na którą założona jest lokata