Operatory matematyczne, funkcje, stałe
• dodawanie
+ , np. 2 + 2
• odejmowanie
- , np. [2, 2] - [3, 4]
• mnożenie
*, np. 2*3
W przypadku macierzy i wektorów symbol * oznacza mnożenie macierzowe! Jeżeli chcemy dokonać zwykłego mnożenie poszczególnych składowych wtedy używamy symbolu .*. Na przykład
v = [1,2,3,4]
a = v.*v
disp(a) //[1, 4, 9, 16]
b = 2*v
disp(b) //[2, 4, 6, 8]
c = v *v'
disp(c) //30
d = v' *v
disp(d)
//1 2 3 4
//2 4 6 8
//3 6 9 12.
//4 8 12 16
• dzielenie
/ , np. 3/7
• potęgowanie
^ lub .^ np. 3^2, [2, 3]^2
• pierwiastkowanie
sqrt, np. sqrt(2.0) sqrt([9, 4])
• wartość bezwzględna, moduł liczby
abs, np. abs(-5.5)
• liczba $e$ (Eulera) i liczba $\pi$
%e, %pi
• funkcje trygonometryczne $\sin \cos \tan$
sin(%pi); cos(3*%pi); cos(2.5)
# Przykład
Zapisz następujące wyrażenia
$$a = \cfrac{2\sqrt{3} + 5^3}{(4+2)(1+\pi)}$$ $$b = \cfrac{2\sqrt[3]{11.5}}{4+e^3} +8.2$$ $$c = \sin^2\left( \cfrac{3}{4}\pi\right) + \cfrac{2.5}{3+\cos^3\left( \cfrac{7}{3}\pi\right) }$$Funkcje macierzowe
• linspace(a,b,c) definicja wektora, początek, koniec, liczba elementów
f = linspace(1,10,10)
disp(f)
• zeros(n,m) macierz wypełniona zerami, podajemy dwa argumenty liczbę wierszy oraz liczbę kolumn
g = zeros(5,5)
disp(g)
• ones(n,m) macierz wypełnione jedynkami, podajemy dwa argumenty liczbę wierzy oraz liczbę kolumn
h = ones(4,5)
disp(h)
• rand(n,m) losowa macierz o wymiarach n $\times$ m
f = rand(2,3)
disp(f)
• eye(n,m) macierz diagonalna (jedynki na przekątnej głównej), podajemy dwa argumenty liczbę wierzy oraz liczbę kolumn
d = eye(3,4)
disp(d)
• length(a) długosć wektora a
a = 1:5:100
l = length(a)
disp(l)
# Przykład
Podstaw pod zmienną A1 tablicę o wymiarach 10x10, której elementy pierwszego i ostatniego wiersza, oraz pierwszej i ostatniej kolumny są jedynkami, pozostałe zerami. Wykorzystaj funkcje zeros() lub ones().
# Przykład
• Podstaw pod zmienną A2 tablicę o wymiarach 10x10 zawierającą w pierwszym wierszu liczby naturalne 10, 9, ..., 1; w ostatnim wierszu liczby naturalne 1, 2, ..., 10; pozostałe elementy to zera
# Przykład
• Podstaw pod zmienną A3 tablicę o wymiarach 10x10 wypełnioną jedynkami. Następnie elementom dla których oba indeksy są nieparzyste, przypisz nową wartość = 5
# Przykład
• Podstaw pod zmienną B1 tablicę o wymiarach 25x25 wypełnioną trójkami. Następnie elementy przekątnej głównej zwiększ o 10. W macierzy B1 elementy kolumn o parzystych indeksach zwiększ o 50.
# Przykład
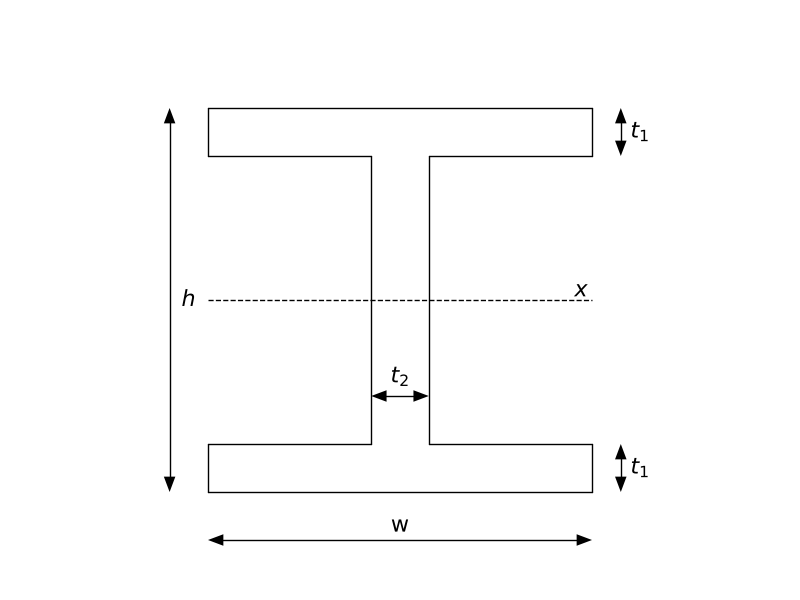
• Opracuj program który oblicza moment bezwładności $I_x$, pole powierzchni $A$ dla dwuteownika jak na rysunku.