Topology optimization of an automotive control arm
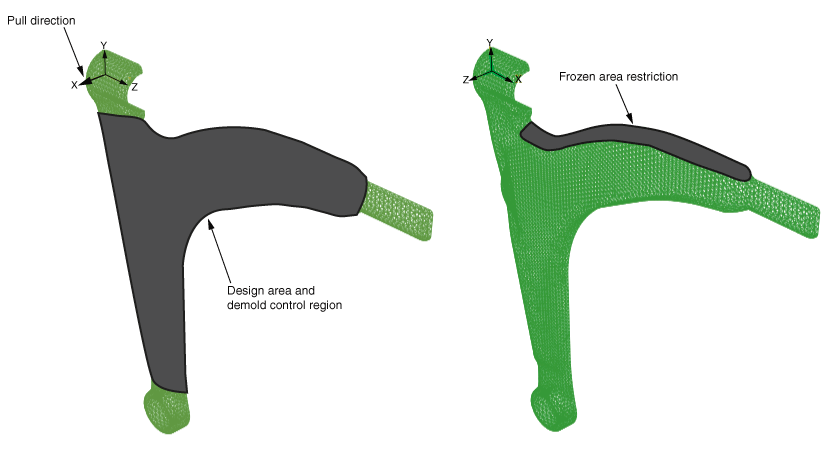
This example illustrates topology optimization of an automotive control arm. During a topology optimization, the material properties of the elements in the design area are modified (effectively removing elements from or adding elements to the Abaqus analysis) until the optimal solution is achieved.

Geometry
The control arm model is a single orphan mesh part that was meshed with quadratic tetrahedral (C3D10) elements. The control arm is symmetric about the X–Y plane, and only one half of the model is studied.
Materials
The control arm is made of an elastic material with a Young's modulus of 210 GPa and a Poisson’s ratio of 0.3.
Boundary conditions and loading
The center of the model is constrained to be symmetric about the Y–Z plane. The upper left and upper right ends of the control arm are outside the design area and are fixed in all three translation degrees of freedom. The lower bearing center is also outside the design area, and its translation is constrained along the z-direction.
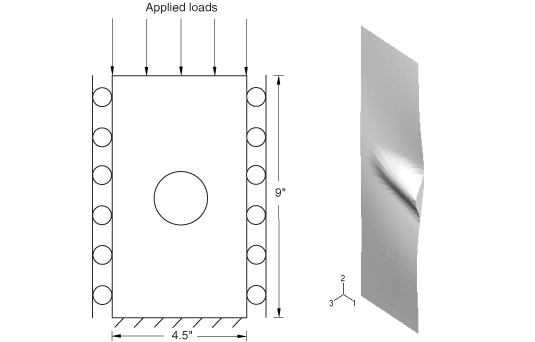
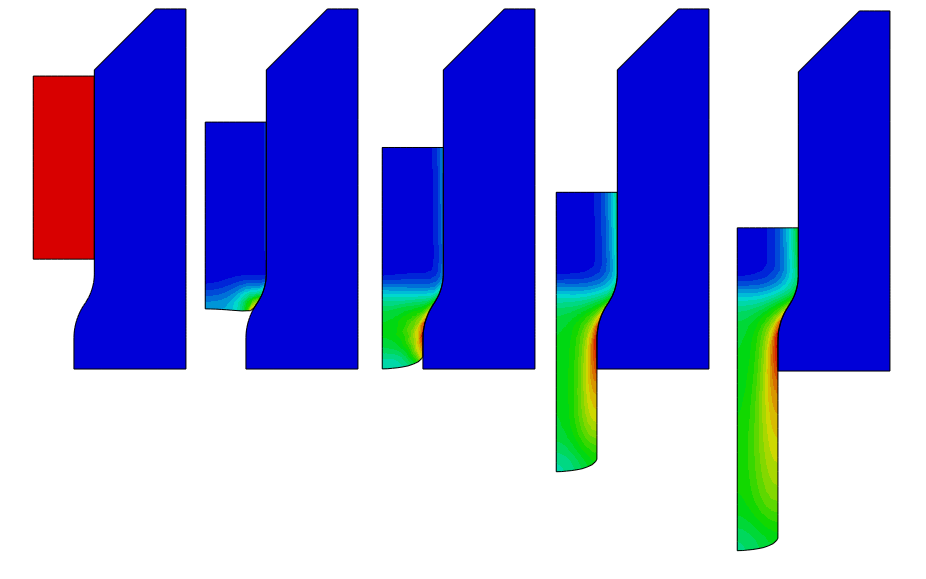
Indentation of a thick plate
This example illustrates the use of adaptive meshing and distortion control in deep indentation problems. A deep indentation problem is solved for axisymmetric geometrie, as shown in Figure. The model consists of a rigid punch and a deformable blank. The punch has a semicircular nose section. The blank is modeled as a crushable foam with the elastic response.
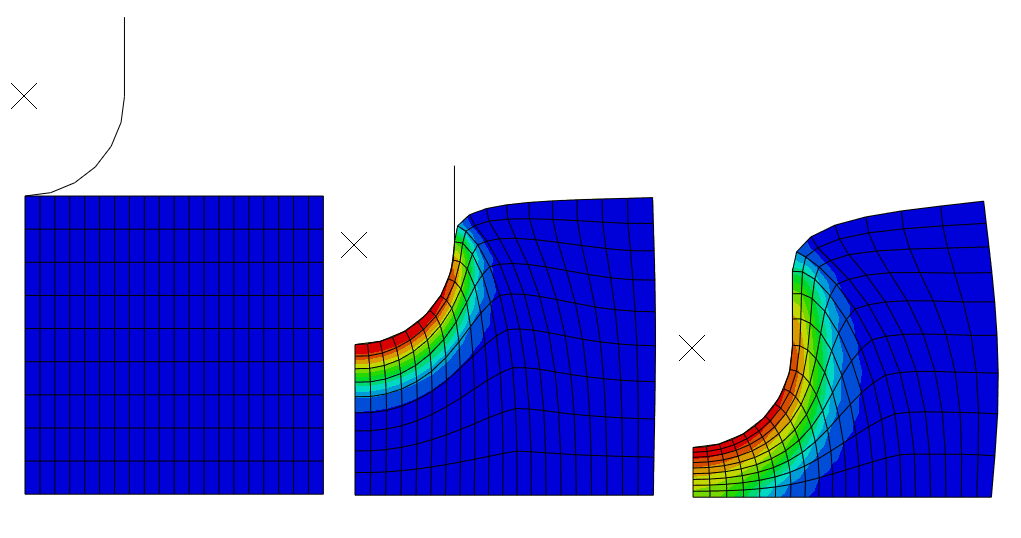
The punch is fully constrained except in the vertical direction. A deep indentation is made by moving the punch into the blank to a depth of 250 mm when adaptive meshing is used and to a depth of 285 mm when distortion control is used. The displacement of the punch is prescribed using a smooth-step amplitude so that a quasi-static response is generated.
Energy computations in a contact analysis
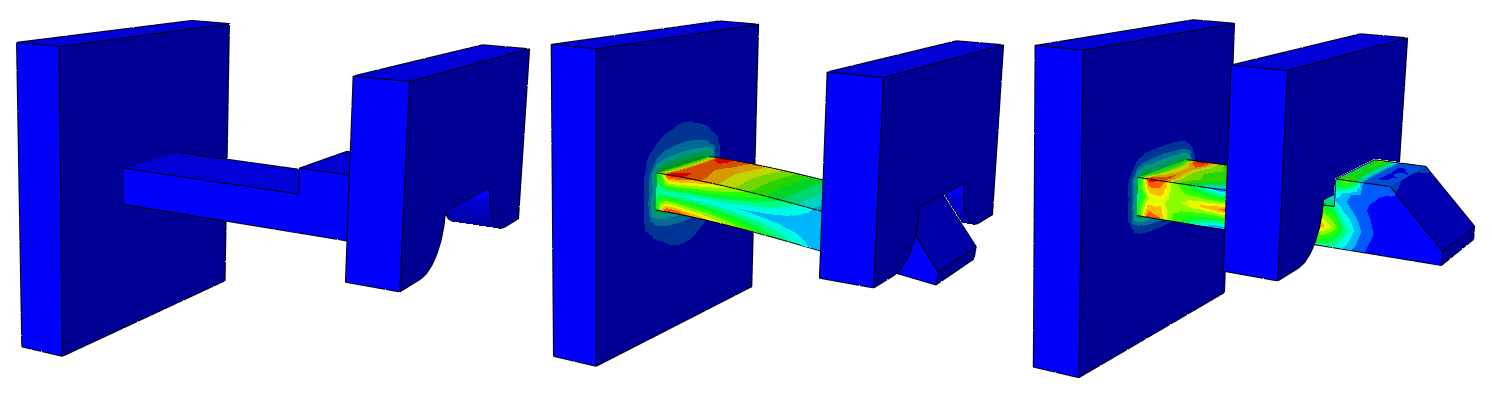
This example shows the contact problem in a static nonlinear elastic, finite-sliding, frictional contact analysis. The model represents a clamped snapping arrowhead that passes through an opening under a wall when pushed by a prescribed x-displacement. The geometry and mesh of C3D8R elements.
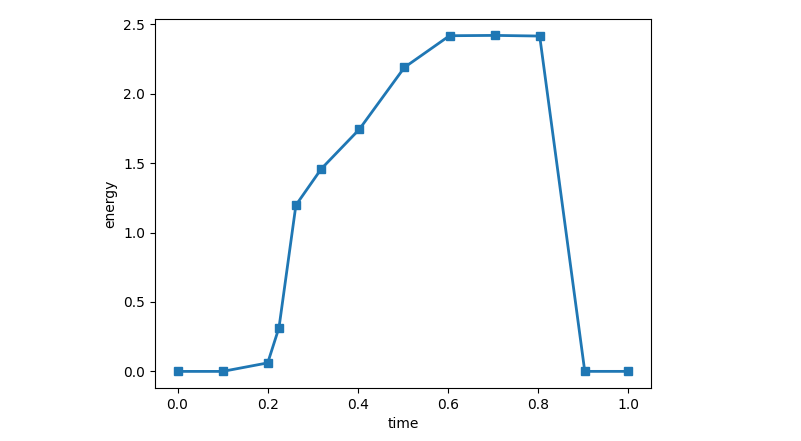
Internal energy
The internal energy $E_I$ is the sum of the recoverable elastic strain energy $E_E$; the energy dissipated through inelastic processes such as plasticity, $E_P$ ; the energy dissipated through viscoelasticity or creep, $E_{CD}$ ; and the artificial strain energy, $E_A$:
$$E_I = E_E + E_P+ E_{CD} + E_A$$The artificial strain energy $E_A$ includes energy stored in hourglass resistances and transverse shear in shell and beam elements. Large values of artificial strain energy indicate that mesh refinement or other changes to the mesh are necessary.
Postbuckling and growth of delaminations in composite panels
This example illustrates the application of the use of fracture criterion in baqus/Standard to predict the postbuckling response, onset, and growth of delaminations in laminated composite panels. Delaminations are a primary failure mode for laminated composite materials. The delamination growth is more prominent under compressive loading since it results in buckling of a sublaminate leading to the delamination growth.
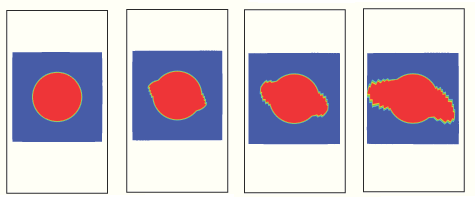
Deep drawing of a square box
This example illustrates the forming of a three-dimensional shape by a deep drawing process.
Rigid projectile impacting eroding plate
This example illustrates impact, progressive failure, and the use of infinite elements. The example simulates the oblique impact of a rigid spherical projectile onto a flat armor plate. A failure model is used for the plate, thus allowing the projectile to perforate the plate.

Progressive failure analysis of thin-wall aluminum extrusion under quasi-static load
In this example problem we consider the overall deformation and failure behavior of a thin-wall, double-chambered aluminum extrusion under quasi-static three-point bending and dynamic axial loading conditions.
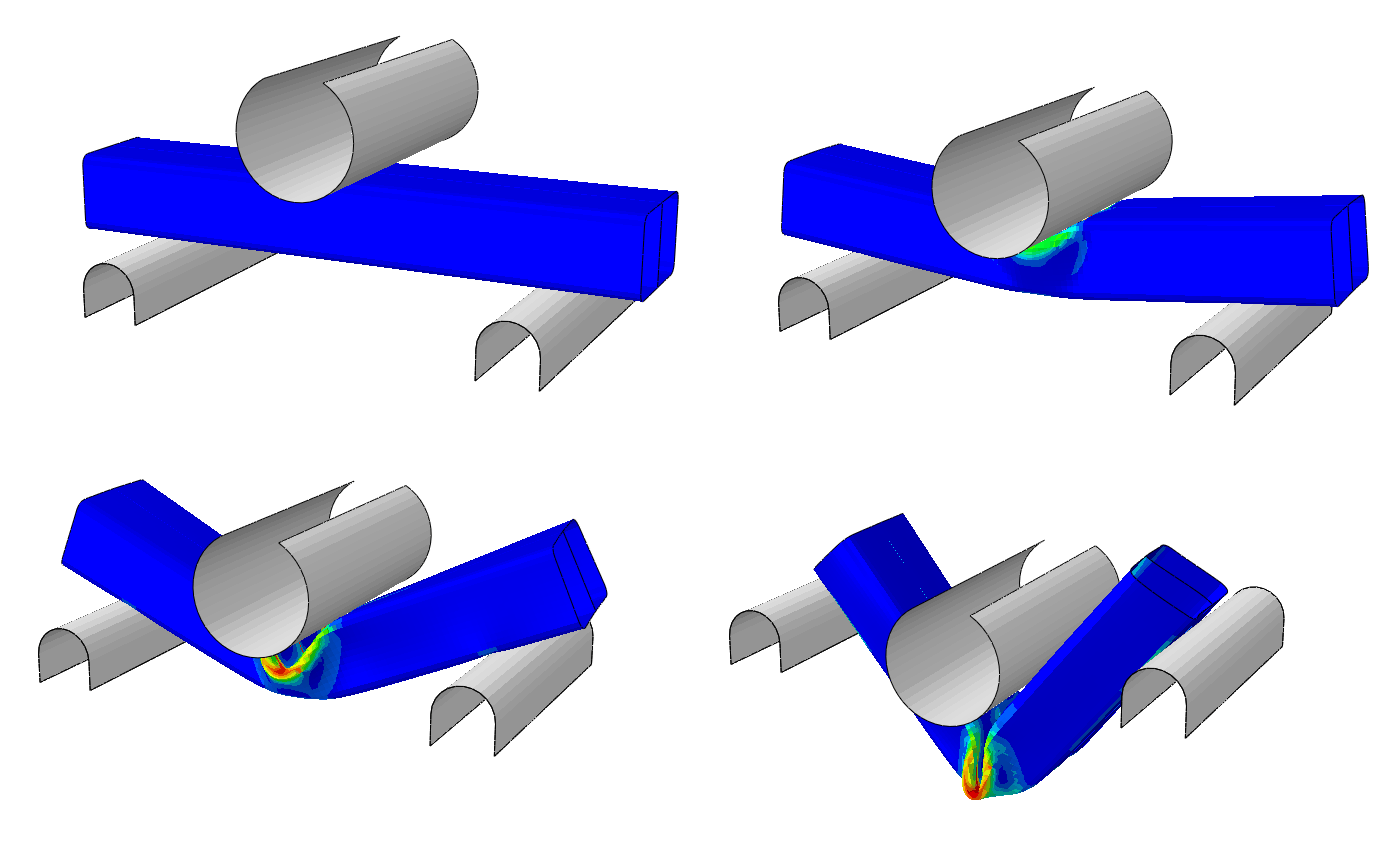
Progressive failure analysis of thin-wall aluminum extrusion under dynamic load
In the axial crushing simulation a velocity initial condition is specified at the reference node of the planar rigid impactor. All the degrees of freedom at the reference node associated with the rigid support are constrained. The axial crushing analyses consist of one explicit dynamic step.
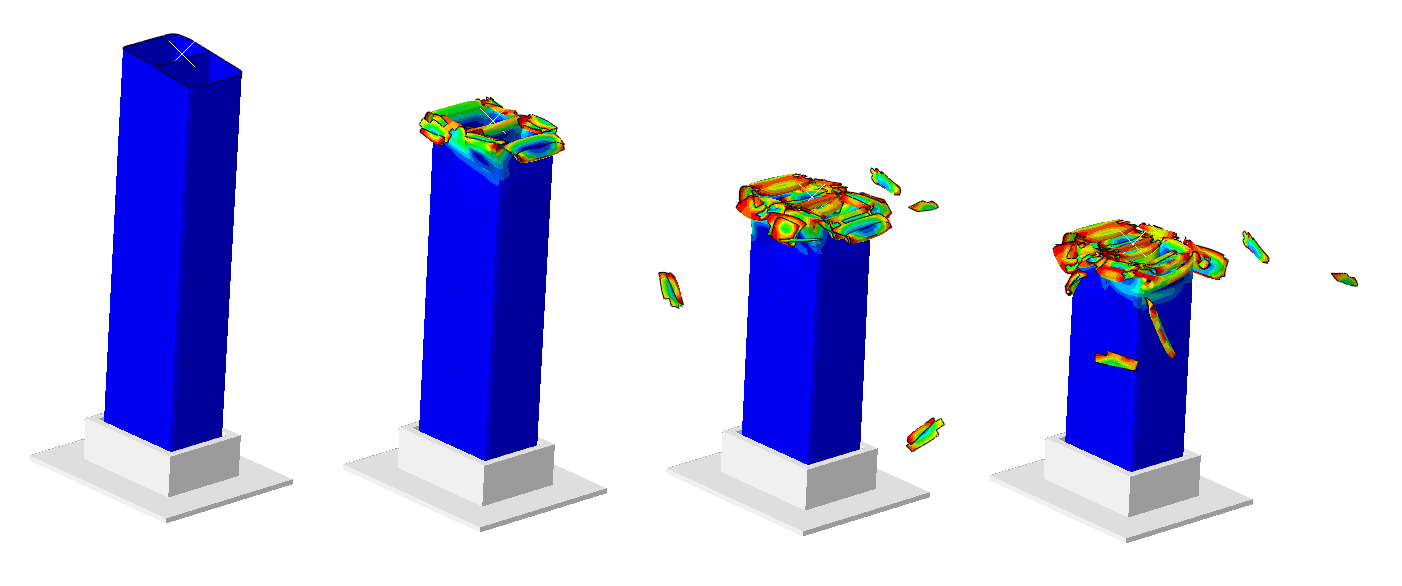
Oblique impact of a copper rod
This example simulates a high velocity, oblique impact of a copper rod into a rigid wall. Extremely high plastic strains develop at the crushed end of the rod, resulting in severe local mesh distortion. Adaptive meshing is used to reduce element distortion and to obtain an accurate and economical solution to the problem.
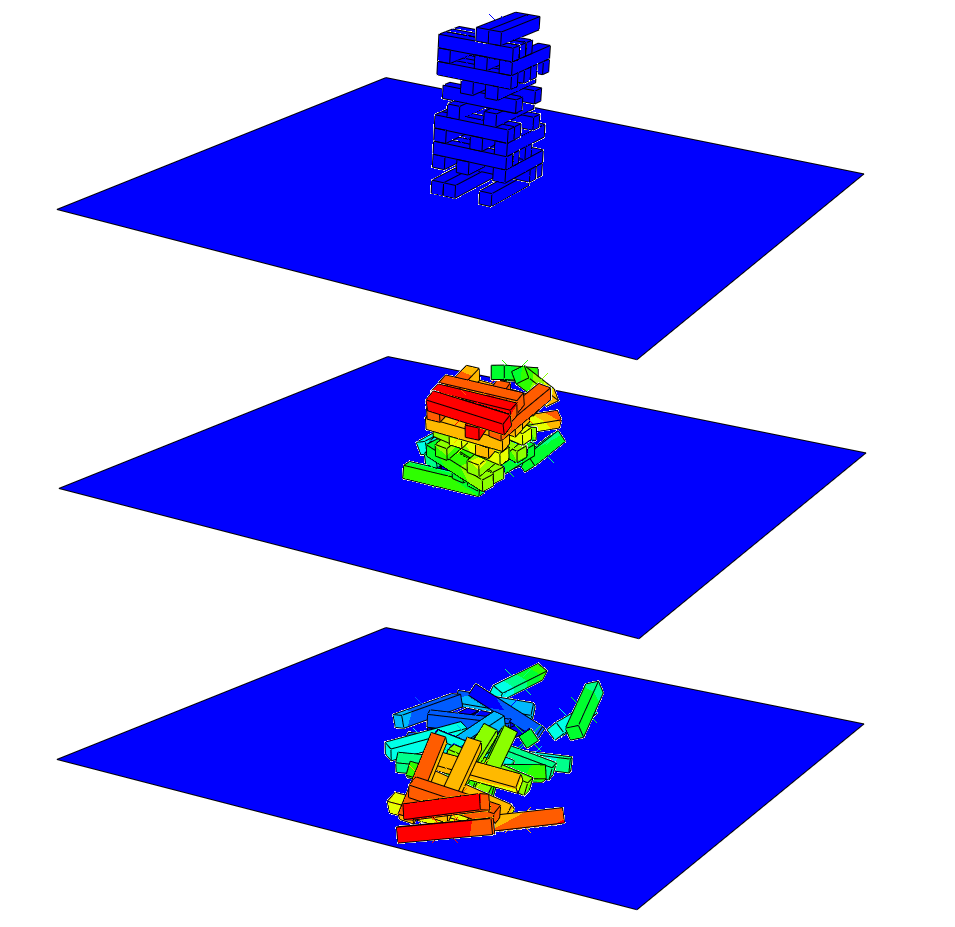
Collapse of a stack of blocks with general contact
This example illustrates the use of the general contact capability in a simulation involving a large number of contacting bodies. The general contact algorithm allows very simple definitions of contact with very few restrictions on the types of surfaces involved.
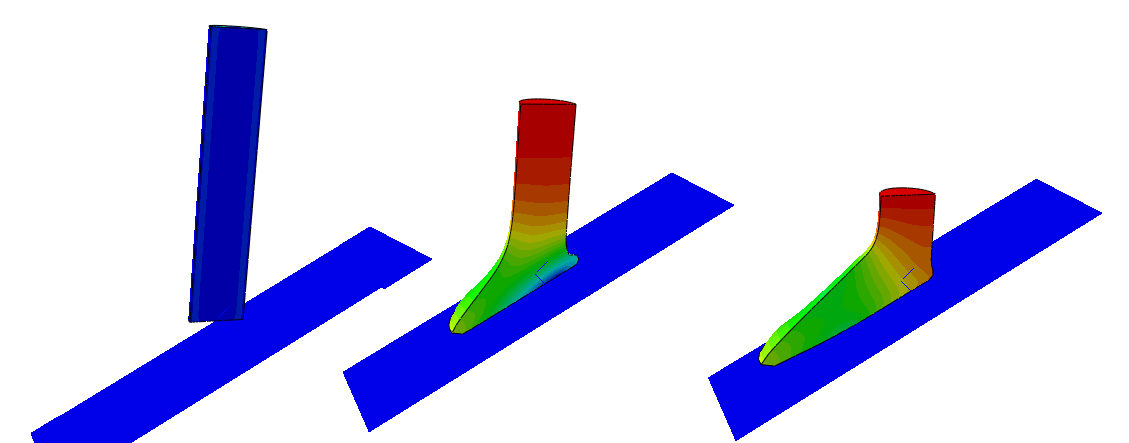
Extrusion of a cylindrical metal bar with frictional heat generation
This example shows how to simulate extrusion problems using Abaqus. In this particular problem the radius of an aluminum cylindrical bar is reduced 33% by an extrusion process. The generation of heat due to plastic dissipation inside the bar and the frictional heat generation at the workpiece/die interface are considered.
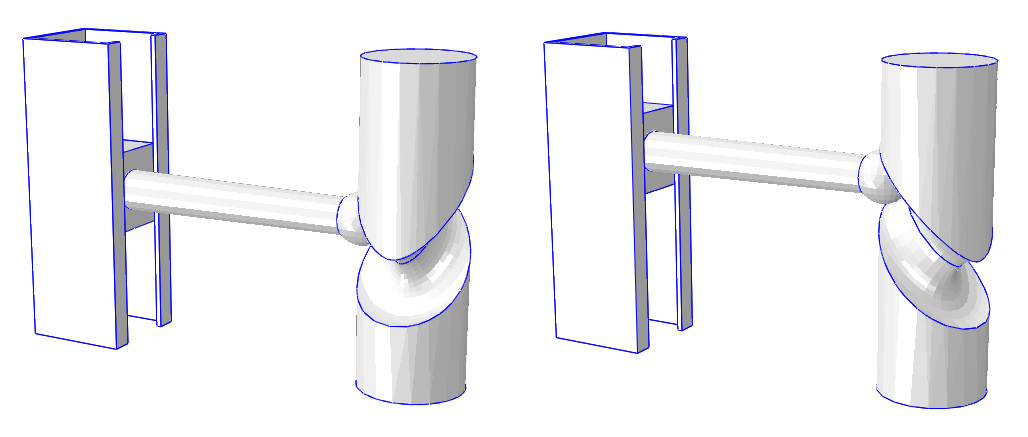
Cylinder-cam mechanism
This example illustrates the use of connector elements to model a cylinder-cam mechanism.
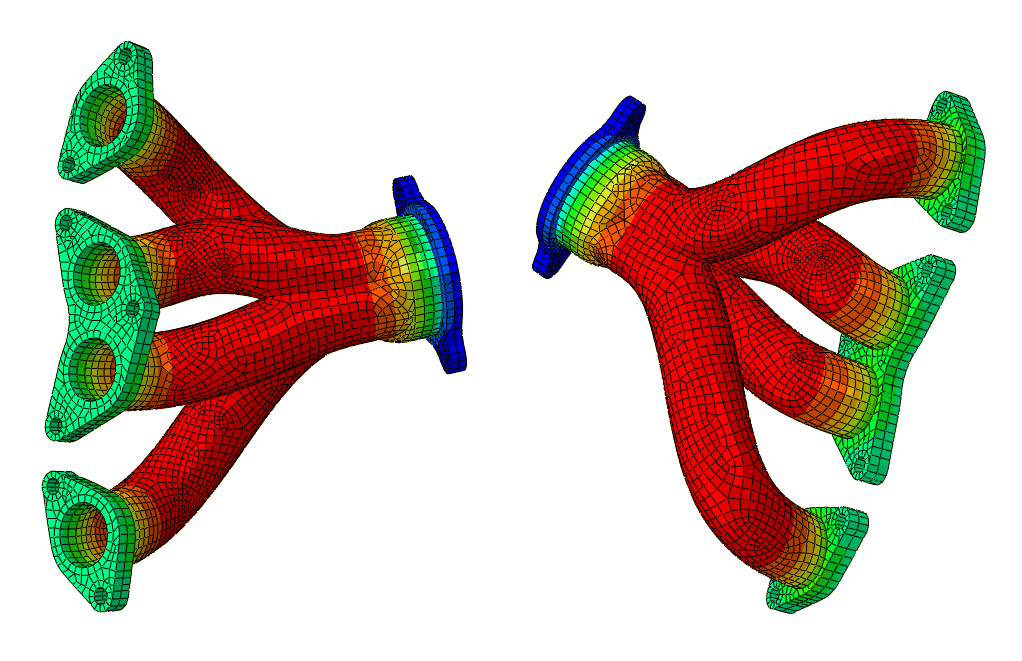
Conductive, convective, and radiative heat transfer in an exhaust manifold
Heat transfer in engine exhaust manifolds is governed by three effects: conduction through the metal, convection from the hot exhaust gases, and radiative exchange between different parts of the metal surface. This example illustrates the computation of the equilibrium thermal state of a manifold subject to these effects