Introduction
"Coupled Eulerian-Lagrangian" (CEL) refers to a type of analysis that involves the interaction between materials in Eulerian and Lagrangian reference frames. The Eulerian frame is fixed in space, while the Lagrangian frame moves with the material. This type of analysis is useful for simulating problems where there is a significant relative motion between materials.
Examples


Eulerian analyses
Pure Eulerian analysis is a finite element technique in which materials are allowed to flow across element boundaries in a rigid mesh. In the more traditional finite element formulation (also known as the Lagrangian technique), materials are closely associated with an element, and the materials move only with the deformation of the mesh.
Eulerian technique can be very effective at treating problems involving very large deformations, material damage, or fluid materials. Eulerian analysis can be performed only in Dynamic Explicit step.
The Eulerian analysis technique can be coupled with traditional Lagrangian techniques to extend the simulation functionality in Abaqus:
• Arbitrary Lagrangian-Eulerian (ALE) adaptive meshing is a technique that combines features of Lagrangian and Eulerian analysis within the same part mesh.
• Coupled Eulerian-Lagrangian (CEL) analysis allows Eulerian and Lagrangian bodies within the same model to interact.
Creating Eulerian models
The procedure for creating Eulerian models in Abaqus/CAE involves the following general steps:
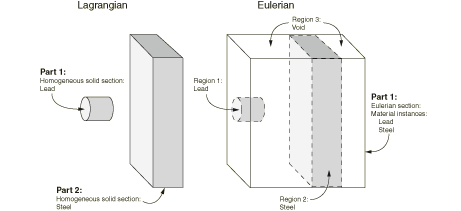
Part Create an Eulerian-type part that defines the geometric region within which Eulerian materials can flow. In the Part module, you may want to create partitions that represent the initial boundaries between different materials in the part.
Material Any material model can be used.
Section In the Property module, define and assign an Eulerian section for the model. The Eulerian section determines which materials can be present in the Eulerian part.
Assembly In the Assembly module, create an instance of the Eulerian part.
Step In the Step module, create a field output request for output variable EVF. This output is necessary to view the deformation of materials in an Eulerian model.
Load In the Load module, create a material assignment predefined field that defines the topology of materials in the initial configuration of the Eulerian part instance. Because the mesh in an Eulerian part is rigid, traditional Lagrangian prescribed conditions do not move with the material deformations loads and boundary conditions are imposed on any material that occupies (or moves into) the region to which the condition is prescribed.
Mesh In the Mesh module, create a hexagonal mesh for the Eulerian part. EC3D8R elements are assigned to the mesh by default.
Coupled Eulerian-Lagrangian (CEL)
Abaqus allows you to create models that include both Eulerian part instances and Lagrangian part instances. During a coupled Eulerian-Lagrangian analysis, the Lagrangian mesh interacts with the materials in the Eulerian part.
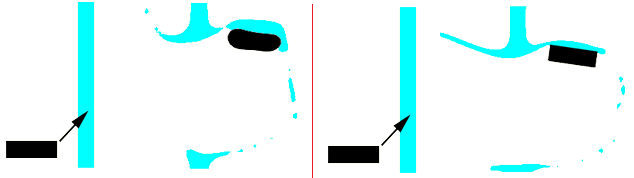
In the Eulerian analysis the water tends to adhere to the sides of the brick, and the brick appears deformed in the final configuration. This apparent deformation is a result of the material volume fraction calculations used for Eulerian materials.
Contact in CEL
Contact in a coupled Eulerian-Lagrangian analysis must be defined using general contact. The general contact definition enables interactions between Lagrangian part surfaces and the surfaces of Eulerian material instances; contact between different Lagrangian parts in the model is also enabled.
Assigning materials to Eulerian part instances
In a pure Lagrangian analysis a section definition includes a reference to a single material. The geometry of the region or element, therefore, defines the geometry of the material.
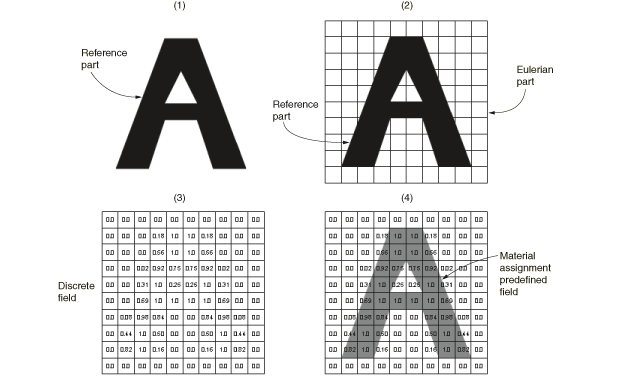
In a pure Eulerian analysis the relationship between the section definition and material is fundamentally different. An Eulerian section definition can reference a list of materials. The part is initially empty of material. To introduce material to the initial state of an Eulerian part, you must use a material assignment predefined field.
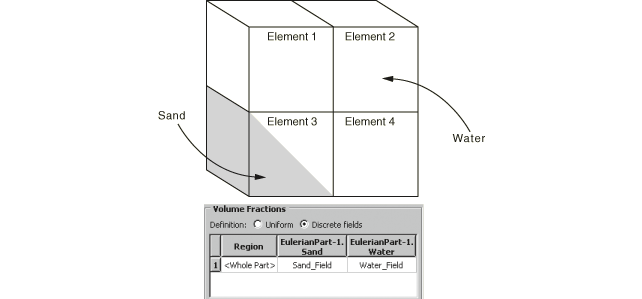
The volume fraction tool creates a scalar discrete field by performing a Boolean comparison between an Eulerian part instance and a second part instance (the reference part instance) that intersects the Eulerian instance.
Eulerian mesh motion
Eulerian mesh motion is a technique that allows to reduce the size of an Eulerian mesh for certain models, thereby improving the performance of the analysis. In some cases the Eulerian domain at the beginning of an analysis does not sufficiently capture the deformations in the model by the end of the analysis.
Abaqus/CAE Usage:
Load module: BC->Create, Category: Other, Types for Selected Step: Eulerian mesh motion
Adaptive mesh refinement
The adaptive mesh refinement feature can locally refine the mesh by subdividing elements identified by user-defined criteria. This refinement can be removed automatically during the analysis once the criteria are no longer satisfied.
Eulerian material advection
As material flows through an Eulerian mesh, state variables are transferred between elements by advection. The variables are assumed to be linear or constant in each old element.
Second-order advection assumes a linear distribution of the variable in each old element. To construct the linear distribution, a quadratic interpolation is constructed from the constant values at the integration points of the middle element and its adjacent elements. Second-order advection is used by default.
First-order advection assumes a constant value of the variable in each old element. This method is simple and computationally efficient however, it tends to diffuse sharp gradients over time. Therefore, this technique should be used only as a computationally efficient alternative for quasi-static simulations.
Arbitrary Lagrangian-Eulerian adaptive meshing
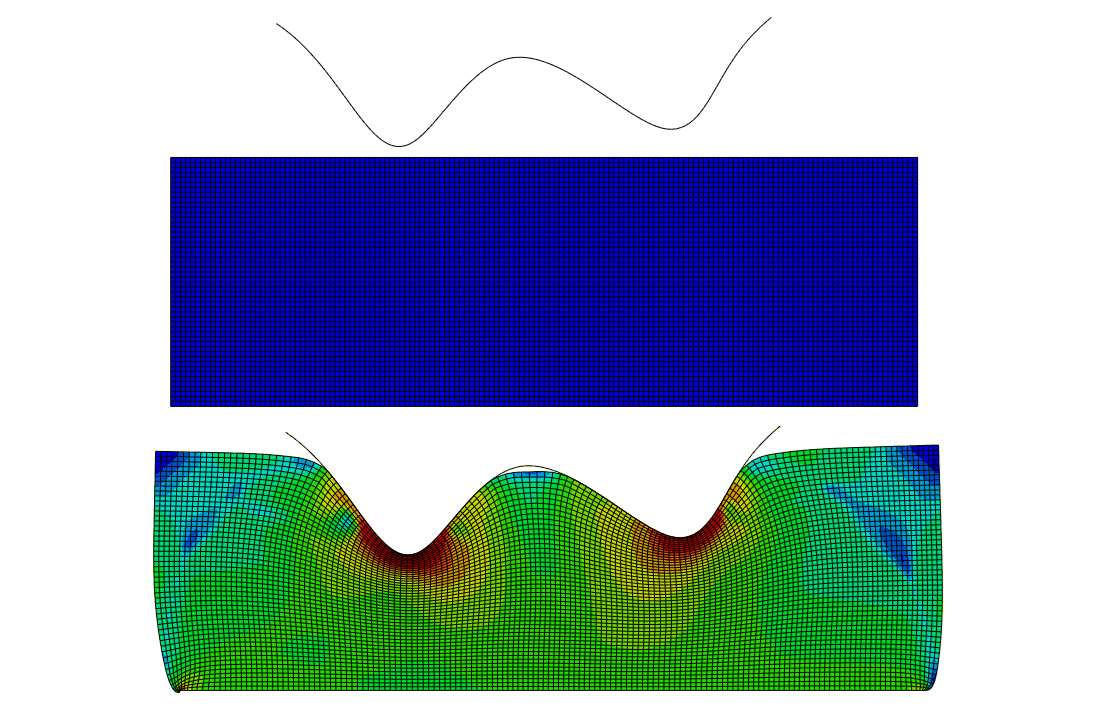
ALE adaptive meshing is a tool that makes it possible to maintain a high-quality mesh throughout an analysis, even when large deformation or loss of material occurs, by allowing the mesh to move independently of the material.
To illustrate the value of adaptive meshing, simple examples of transient and steady-state forming applications follow.
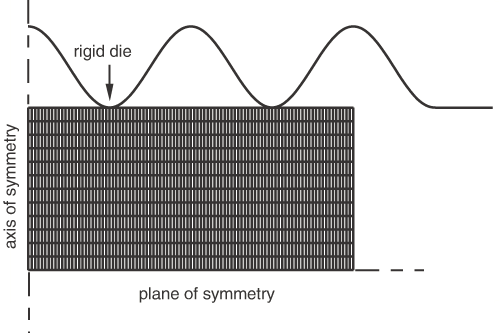
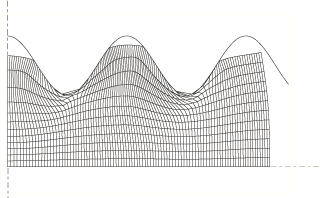
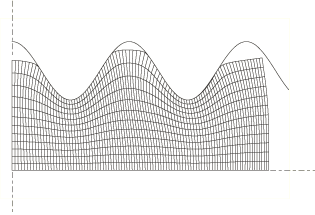
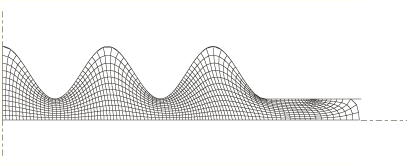
Example: