Metal Plasticity
Basic Assumptions
• metals deform elastically when they are subjected to small strains, the elastic deformation is linear
• metal materials deform plastically (yield) when they are subjected to higher stresses, the yield strength of metals is independent of the hydrostatic pressure
• the plastic defromation of metals is approximetely incompressible
The basic components of an icrremental plasticity model are:
• strain rate decomposition, the total strain rate is assumed to be a combination of the elastic strain rate $\dot{\ee}^e$ and the irreversible plastic strain rate $\dot{\ee}^{pl} $
$$\dot{\ee} = \dot{\ee}^e + \dot{\ee}^{pl}$$• yield function $f(\ss, \sigma^0)$ defines when the metal begins to deform inelastically, when $f=0$ the metal is yielding. The yield function is often written in terms of stress invariants.
There are two yield functions available for the classical metal plasticity:
• The Mises yield function,
$$f = q - \sigma^0, \quad q = \sqrt{\cfrac{3}{2}(\S \cdot \S)}, \quad \S = \ss + p\I, \quad p = -\cfrac13 tr(\ss)$$• Hill's anisotropic yield function
$$f = \sqrt{F(\sigma_{22}-\sigma_{33})^2 + G(\sigma_{33}-\sigma_{11})^2 + H(\sigma_{11}-\sigma_{22})^2 + 2L\sigma_{23} + 2M\sigma_{13}^2 + 2N\sigma_{12}^2 } - \sigma^0$$where $F$, $G$, $H$, $L$, $M$ and $N$ are material constants.
• flow rule, Abaqus uses associated plastic flow rule. Therefore, as the material yields, the inelastic deformation rate is in the direction of the normal to the yield surface (the plastic deformation is volume invariant).
$$\dot{\ee}^{pl} = \dot{\lambda}\pp{g}{\ss}, \quad g=f$$• evolution (hardening) laws, in Abaqus there are five hadeining models availble
1) perfect plasticity - the yield function $f$ does not evolve as the metal accumulates plastic strains. Perfect plasticity is defined by providing only one value for the yield stress $\sigma^0$
2) isotropic hardening - the yield stress evolves as the metal accumulates plastic strains
$$\sigma^0 = \sigma^0(\bar{\varepsilon}^{pl}), \quad \bar{\varepsilon}^{pl} = \int_0^t\left( \sqrt{\cfrac{2}{3}\dot{\ee}^{pl}\cdot \dot{\ee}^{pl}}\right)dt$$3) linear kinematic hardening is used to model the behavior of metals subjected to cyclic loading
$$f = q(\ss-\boldsymbol{\alpha}) - \sigma^0 = 0$$where $\boldsymbol{\alpha}$ is the backstress tensor that describes how the center of the yield sufrace moves in stress space as plastic strains accumulates
4) nonlinear combined isotropic-kinematic hardening is the most general law and defines the yield functions as
$$f= q(\ss-\boldsymbol{\alpha}) - \sigma^0(\bar{\varepsilon}^{pl}) = 0$$5) Johnson Cook plasticity is a particular type of Mises plasticity model with analytical forms of the hardening law
$$\sigma^0 = \left[ A+B (\bar{\varepsilon}^{pl})^n\right]\left( 1-\bar{\theta}^m \right)$$where $\bar{\varepsilon}^{pl}$ is the equivalent plastic strain and $A$, $B$, $n$ and $m$ are material parameters. $\bar{\theta}$ is the nondimensional temperature.
Components commonly added to plasticity models include
• rate dependence $\sigma^0(\dot{\bar{\varepsilon}}^{pl})$
• temperature dependence $\sigma^0(\theta)$
• heat generation, in an adiabatic analysis plastic straining gives rise to a heat flux per unit volume
$$r^{pl} = \eta \ss \cdot \dot{\ee}^{pl}$$$where $r^{pl}$ is the heat flux that is added into the thermal energy balance, $\eta$ is the user-specified inelastic heat fraction (assumed constant).
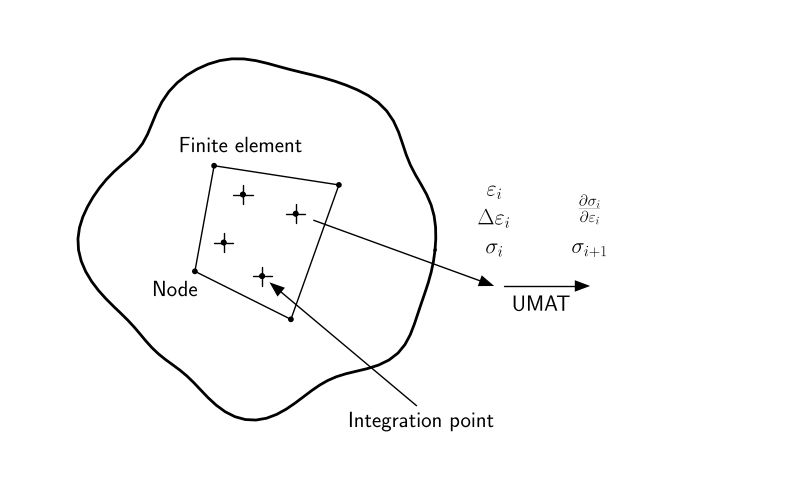
User Material UMAT, VUMAT
ABAQUS/Standard and ABAQUS/Explicit have interfaces that allow the user to implement general constitutive equations.
• In ABAQUS/Standard the user-defined material model is implemented in user subroutine UMAT.
• In ABAQUS/Explicit the user-defined material model is implemented in user subroutine VUMAT.
Use UMAT and VUMAT when none of the existing material models included in the ABAQUS material library accurately represents the behavior of the material to be modeled.
The main difference between UMAT and VUMAT is that UMAT is for implicit analysis and VUMAT is for explicit analysis. This means that UMAT requires updating the material Jacobian or stiffness matrix at each time step, while VUMAT does not. UMAT also needs the deformation gradient as an input to calculate the global strain, while VUMAT uses the strain increment instead.
User subroutine UMAT
• will be called at all material calculation points of elements for which the material definition includes a user-defined material behavior;
• can use solution-dependent state variables;
• must update the stresses and solution-dependent state variables to their values at the end of the increment for which it is called;
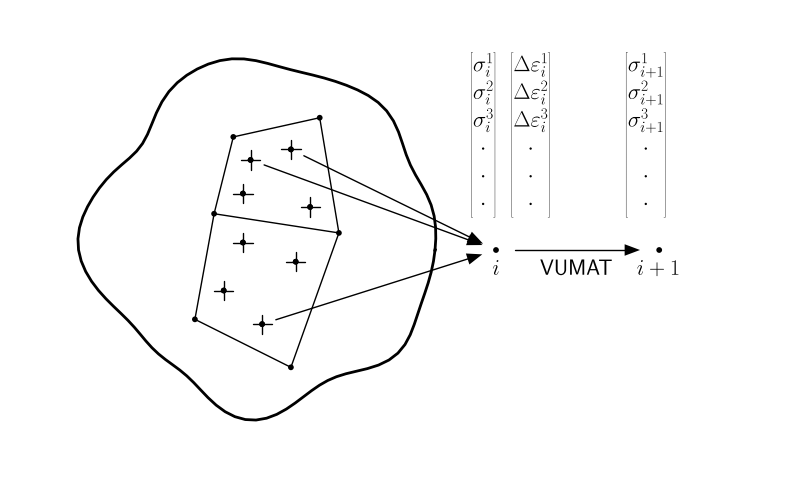
User subroutine VUMAT:
• will be called for blocks of material calculation points for which the material is defined
• can use and update solution-dependent state variables
• can use any field variables that are passed in
User subroutine interface
UMAT
SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
1 RPL,DDSDDT,DRPLDE,DRPLDT,
2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
C
INCLUDE 'ABA_PARAM.INC'
C
CHARACTER*80 CMNAME
DIMENSION STRESS(NTENS),STATEV(NSTATV),
1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
4 JSTEP(4)
C
user coding to define DDSDDE, STRESS, STATEV, SSE, SPD, SCD
and, if necessary, RPL, DDSDDT, DRPLDE, DRPLDT, PNEWDT
C
RETURN
END
VUMAT
SUBROUTINE VUMAT(
C READ ONLY (UNMODIFIABLE)VARIABLES -
1 NBLOCK, NDIR, NSHR, NSTATEV, NFIELDV, NPROPS, LANNEAL,
2 STEPTIME, TOTALTIME, DT, CMNAME, COORDMP, CHARLENGTH,
3 PROPS, DENSITY, STRAININC, RELSPININC,
4 TEMPOLD, STRETCHOLD, DEFGRADOLD, FIELDOLD,
5 STRESSOLD, STATEOLD, ENERINTERNOLD, ENERINELASOLD,
6 TEMPNEW, STRETCHNEW, DEFGRADNEW, FIELDNEW,
C WRITE ONLY (MODIFIABLE) VARIABLES -
7 STRESSNEW, STATENEW, ENERINTERNNEW, ENERINELASNEW )
C
INCLUDE 'VABA_PARAM.INC'
C
DIMENSION PROPS(NPROPS), DENSITY(NBLOCK), COORDMP(NBLOCK,*),
1 CHARLENGTH(NBLOCK), STRAININC(NBLOCK,NDIR+NSHR),
2 RELSPININC(NBLOCK,NSHR), TEMPOLD(NBLOCK),
3 STRETCHOLD(NBLOCK,NDIR+NSHR),
4 DEFGRADOLD(NBLOCK,NDIR+NSHR+NSHR),
5 FIELDOLD(NBLOCK,NFIELDV), STRESSOLD(NBLOCK,NDIR+NSHR),
6 STATEOLD(NBLOCK,NSTATEV), ENERINTERNOLD(NBLOCK),
7 ENERINELASOLD(NBLOCK), TEMPNEW(NBLOCK),
8 STRETCHNEW(NBLOCK,NDIR+NSHR),
8 DEFGRADNEW(NBLOCK,NDIR+NSHR+NSHR),
9 FIELDNEW(NBLOCK,NFIELDV),
1 STRESSNEW(NBLOCK,NDIR+NSHR), STATENEW(NBLOCK,NSTATEV),
2 ENERINTERNNEW(NBLOCK), ENERINELASNEW(NBLOCK),
C
CHARACTER*80 CMNAME
C
DO 100 KM = 1,NBLOCK
USER CODING
100 CONTINUE
c
RETURN
END
Component ordering in tensors
The component ordering depends whether the tensor is symmetric or nonsymmetric. For symmetric tensors such as the stress and strain tensors, there are NDIR+NSHR component
| Component | 2D Case | 3D Case |
|---|---|---|
| 1 | $\sigma_{11}$ | $\sigma_{11}$ |
| 2 | $\sigma_{22}$ | $\sigma_{22}$ |
| 3 | $\sigma_{33}$ | $\sigma_{33}$ |
| 4 | $\sigma_{12}$ | $\sigma_{12}$ |
| 5 | $\sigma_{23}$ | |
| 6 | $\sigma_{31}$ |
For nonsymmetric tensors there are NDIR+2*NSHR components
| Component | 2D Case | 3D Case |
|---|---|---|
| 1 | $F_{11}$ | $F_{11}$ |
| 2 | $F_{22}$ | $F_{22}$ |
| 3 | $F_{33}$ | $F_{33}$ |
| 4 | $F_{12}$ | $F_{12}$ |
| 5 | $F_{12}$ | $F_{23}$ |
| 6 | $F_{31}$ | |
| 7 | $F_{21}$ | |
| 8 | $F_{32}$ | |
| 9 | $F_{13}$ |
The shear strain components in user subroutine VUMAT are stored as tensor components and not as engineering components; this is different from user subroutine UMAT in Abaqus/Standard, which uses engineering components.
Since the number of active stress and strain components varies between element types, the routine must be coded to provide for all element types with which it will be used.
| Case | NDIR | NSHR |
|---|---|---|
| 1D | 1 | 0 |
| 2D plane stress | 2 | 1 |
| 2D plane strain | 3 | 1 |
| 2D axisymmetry | 3 | 1 |
| 3D | 3 | 3 |
• NTENS
This is the size of the stress or strain component array and reflects the overall dimension of the Abaqus model into UMAT. For example, that is 6 for a general 3D and 4 for a simplified plane strain (2D) model.
NTENS = NDIR + NSHR
Parameters entered through Abaqus model definition & sent to UMAT/VUMAT
• PROPS (NPROPS)
User-specified array of material constants associated with this user material with NPROPS (number of material constants) elements. When defining our model through Abaqus/CAE, we enter these parameters in Property module.
UMAT variables
Parameters that are available by Abaqus to UMAT
• STRESS(NTENS)
A vector form of stress tensor at the start of increment. It has NTENS elements. For a general 3D model, we need 6 values for stress (3 normal and 3 shear) so this vector will have 6 elements.
• STRAN(NTENS), DSTRAN(NTENS)
STRAN is a vector form of strain tensor at the start of increment. DSTRAN is the increment (variation) of strain.
• TIME(2), DTIME
Respectively, total and incremental values of time. TIME is a 2-element vector; the first element, i.e. TIME(1) states the value of step time and the second, i.e. TIME(2), is the value of total time, both at the beginning of the current increment.
• ...
Parameters that must be calculated and updated by UMAT
• STRESS(NTENS)
• DDSDDE(NTENS,NTENS)
A 2D format of Jacobian matrix with NTENS row and NTENS column called DDSDDE matrix
where, $\Delta \ss$ is the increment in (Cauchy) stress and $\Delta \ee$ is the increment in strain.
VUMAT variables
Parameters that are available by Abaqus to VUMAT
• NBLOCK
Number of material points to be processed in this call to VUMAT.
• STRESSOLD (NBLOCK, NDIR+NSHR)
Stress tensor at each material point at the beginning of the increment.
• ...
Parameters that must be calculated and updated by VUMAT
• STRESSNEW (NBLOCK, NDIR+NSHR)
Stress tensor at each material point at the end of the increment.
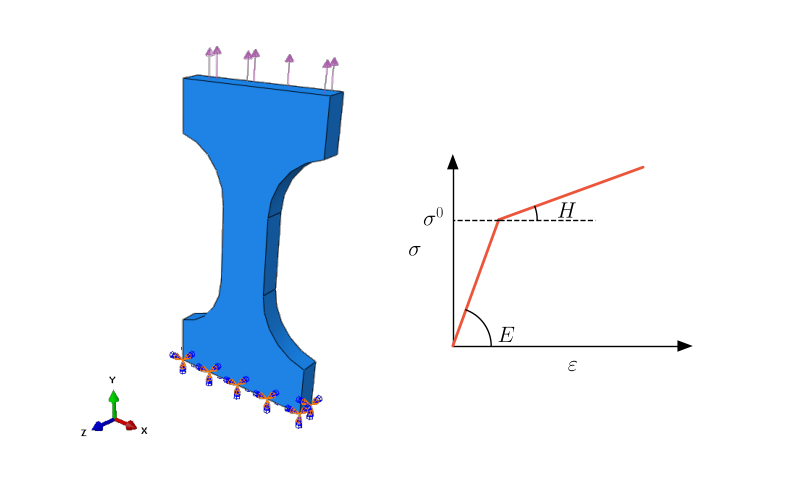
Example 4 Quasi static tension test of dog-bone specimen
The developed example script can be downloaded at: