Płaski stan naprężenia

W mechanice ciał odkształcalnych płaski stan naprężenia oznacza, że stan naprężenia ulega uproszczeniu. Tensor naprężenia jest reprezentowany przez macierz $2\times2 $ zamist pełnej macierzy $3\times 3$.

$$\ss = \mat{ \sigma_{11} }{ \sigma_{12} }{ \sigma_{13} }{ \sigma_{21} }{ \sigma_{22} }{ \sigma_{23} }{ \sigma_{31} }{ \sigma_{32} }{ \sigma_{33} }= \mat{ \sigma_{11} }{ \sigma_{12} }{ 0 }{ \sigma_{21} }{ \sigma_{22} }{ 0 }{ 0 }{ 0 }{ 0 }\quad \rightarrow \quad \ss = \matt{ \sigma_{11} }{ \sigma_{12} }{ \sigma_{21} }{ \sigma_{22} }$$

Rozwiążmy z użyciem biblioteki CALFEM problem ściskania tarczy swobodnie podpartej obciążonej siłą w środku rozpiętości. Zakładamy że matereriał jest sprężysty i izotropowy. Interesuje nas analiza statyczna. Nasze obliczenia prowadzimy w opariuc o teorię małych odkształceń.

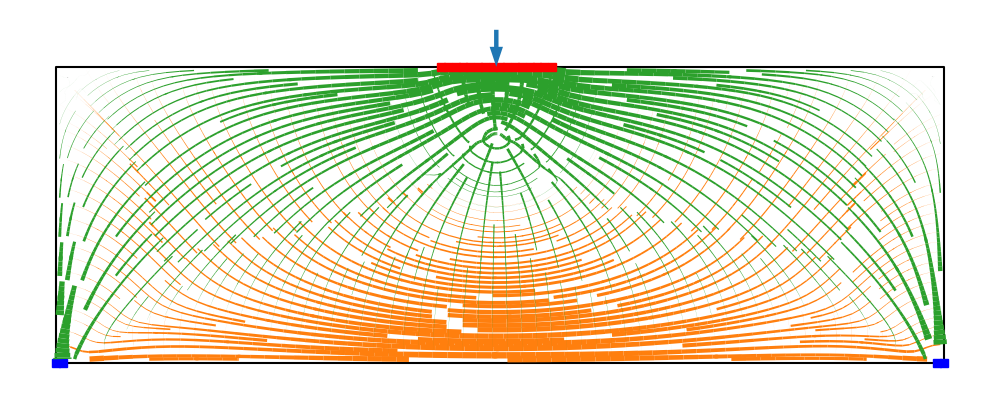
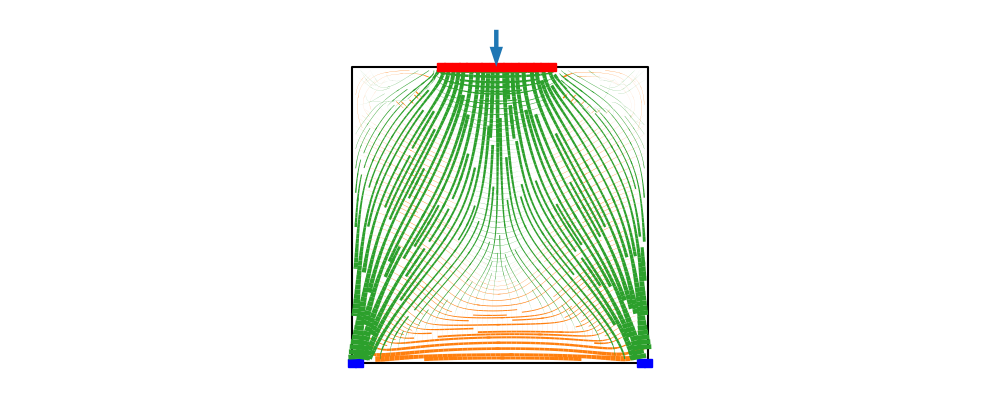
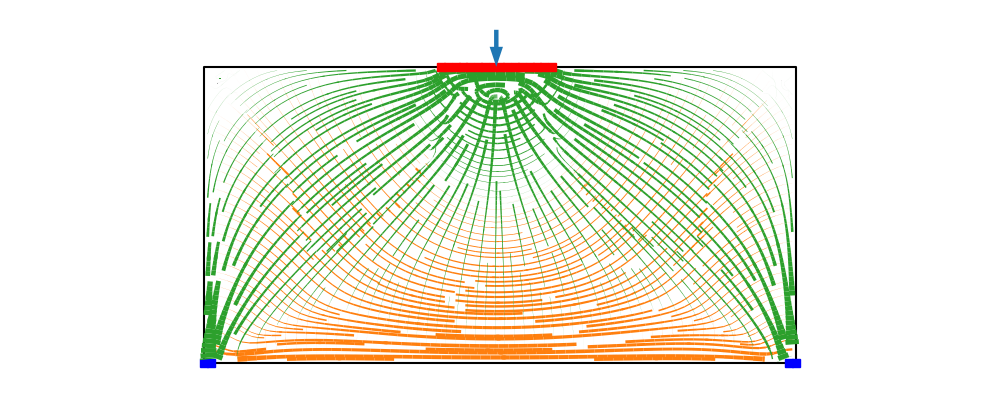
Rozwiązując przedstawione zagadnienie otrzymujemy pole przemieszczenia, które w dalszej kolejności mozemy przeliczyć na pole odkształcenia a następnie używajć zwiazku konstytutuwynego mozemy wyznaczyć pole naprężenie. Jak już wspomniano stan naprężenia w danym punkcie będzie reprezentowany przez 4 składowe. Z uwagi na to że tensor naprężenie jest symetryczne 3 składowe będą niezależne. Dla każdego tensora mozemy rozwiązać zagadnienie własne (wyznaczyć kierunki i wartosci własne). Na poniższych rysunkach przedstawiono wizualizację uzyskanych pól skalarno-wektorowych. Zielone linie i ich grubość odpowiada ujemnym wartosciom własnym i odpowiadajacym im wektorm własnym (ściskanie). Z kolei kolor pomarańczowy oznacza dodatanie wartosci własne i odpowiadajace im wektory własne.

$$\ss = \matt{ \sigma_{11} }{ \sigma_{12} }{ \sigma_{21} }{ \sigma_{22} }\quad \rightarrow \quad \ss = \matt{ \sigma_{1} }{ 0}{ 0 }{ \sigma_{2}}$$

W pierwsze kolejnosci obliczenia zostały przeprowadzone dla tarczy w kształcie kwadratu

Następnie długość tarczy została zwiekszona dwukrotnie, przy zachowaniu tego samego obciażeni

W kolejnym kroku długość tarczy została wydłużona 3-krotnie.

---