Poisson ratio - uniconstant theroy of elasticity

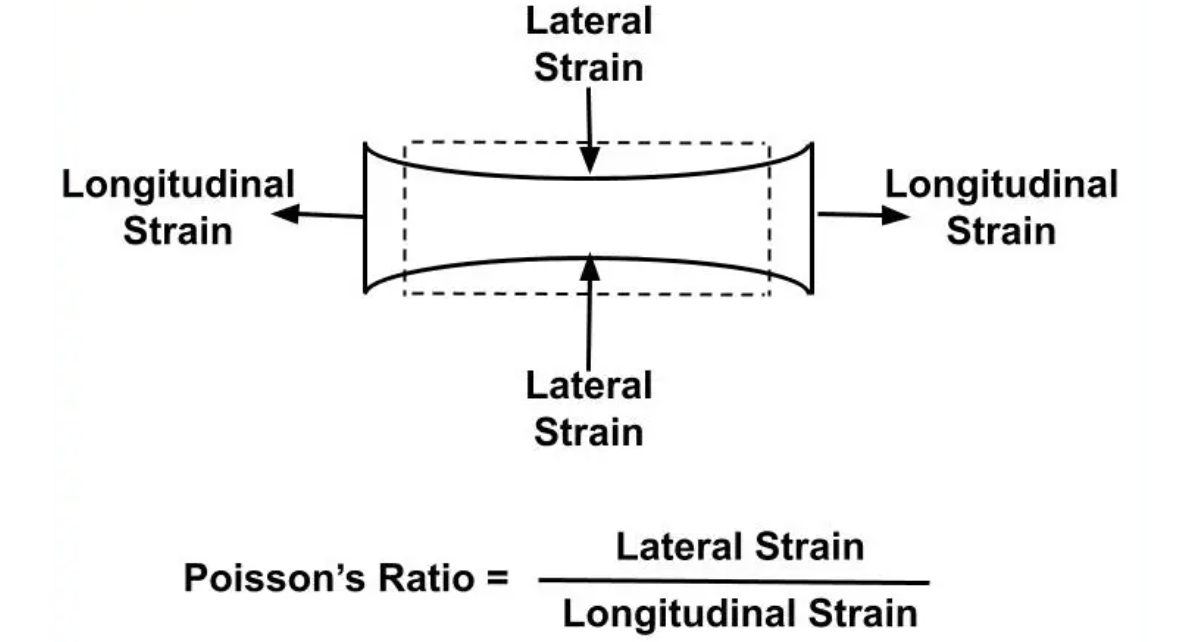
Poisson's ratio is denoted by the Greek letter $\nu$ (nu) and is typically expressed as a dimensionless number between

$$\nu \in (-1 , 0.5)$$

In most materials, Poisson's ratio falls between 0 and 0.5, although it can theoretically range from -1 to 0.5 for some specialized materials.

If Poisson's ratio is close to 0, it means that the material hardly changes in width when stretched or compressed.

If Poisson's ratio is close to 0.5, it means that the material significantly reduces in width when stretched and increases in width when compressed.

In practical terms, materials like rubber typically have higher Poisson's ratios, indicating a significant change in width when stretched. Metals usually have lower Poisson's ratios, indicating minimal changes in width during stretching or compression.

Poisson's ratio is an essential parameter in the study of material mechanics, including elasticity, plasticity, and structural engineering. It plays a crucial role in understanding the behavior of materials under different types of loading conditions and is a critical factor in the design and analysis of various structures and components

Refert na temat modelowania ciał, dlaczego współczynnik Poissona jest równy 0.25 jeżeli modelujemy ciało jako zbiór punktów połączonych sprężynkami.

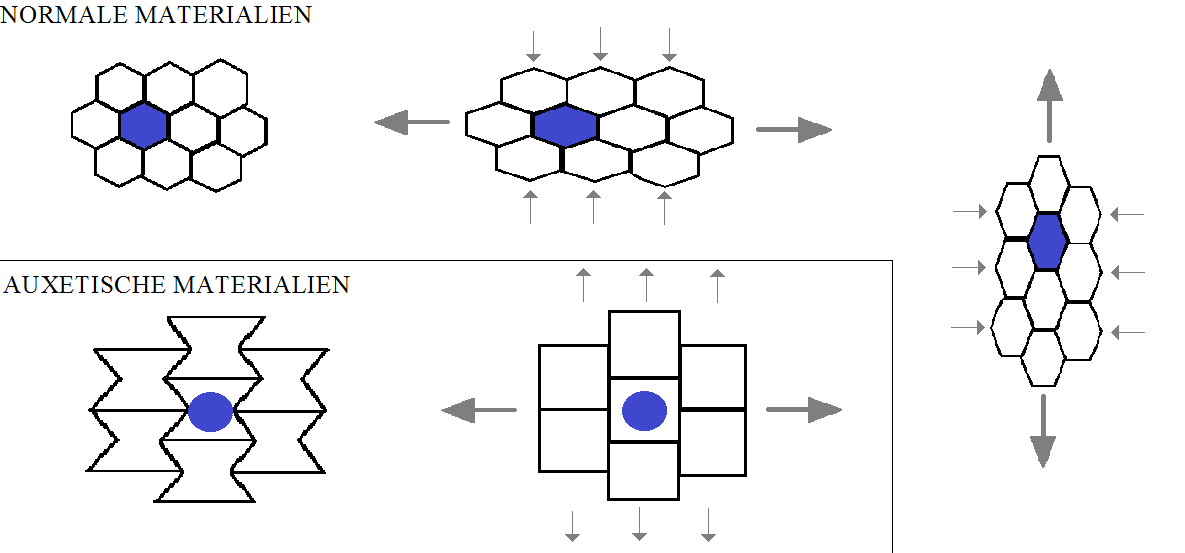
Negative Poisson's ratio

A negative Poisson's ratio, also known as auxetic behavior, describes a material that expands in lateral dimensions when stretched along its longitudinal axis, which is quite unusual compared to the typical behavior of materials. In other words, when you stretch a material with a negative Poisson's ratio, it gets wider, rather than narrower, as you might expect with most materials.

Materials with negative Poisson's ratios exhibit unique mechanical properties that can be advantageous for specific applications. For instance:

• Impact Absorption: Auxetic materials can be effective in absorbing impact energy due to their ability to expand laterally upon deformation. This property makes them potentially useful in applications such as protective gear and shock-absorbing materials.

• Increased Friction: Some auxetic materials can increase friction under certain conditions, making them suitable for applications like shoe soles or gripping surfaces.

• Improved Mechanical Stability: Auxetic structures may offer enhanced stability and resistance to deformation under certain loading conditions, which can be beneficial in engineering and structural applications.

Researchers and engineers are exploring the potential of auxetic materials for various technological advancements, but their practical implementation often faces challenges related to manufacturing, scalability, and optimization for specific applications. Nonetheless, the unique properties of materials with negative Poisson's ratios continue to intrigue scientists and engineers in their quest for innovative materials and designs.